В статистической практике также находят применение степенные средние 3-го и более высоких порядков.

4. ПОКАЗАТЕЛИ ВАРИАЦИИ И АНАЛИЗ ЧАСТОТНЫХ РАСПРЕДЕЛЕНИЙ

4.1. Показатели вариации

Рассматривая зарегистрированные в процессе статистического наблюдения величины того или иного признака у отдельных еди­ниц совокупности, можно обнаружить между ними различия.

Колеблемость, многообразие, изменяемость величины признака у единиц совокупности называются вариацией. Вариация порождается комплексом условий, действующих на совокупность и ее единицы. Например, вариация оценок на экза­мене в вузе порождается, в частности, различными способностя­ми студентов, временем, затрачиваемым ими на самостоятельную работу, различием социально-бытовых условий и т. д. Именно ва­риация и предопределяет необходимость статистики. Если бы все студенты получали одинаковые оценки или, например, семьи име­ли одинаковые доходы, то необходимость в статистическом иссле­довании отпала бы.

По степени вариации можно судить о многих сторонах процес­са развития изучаемых явлений, в частности об однородности со­вокупности, устойчивости индивидуальных значений признака, типичности средней, о взаимосвязи между признаками одного и того же явления и признаками разных явлений. На основе показателей вариации в статистике разрабатываются другие по­казатели и методы изучения явлений и процессов общественной жизни – показатели тесноты связи между явлениями и их призна­ками, показатели оценки точности выборочного наблюдения.

Средние, описанные в предыдущей главе, являются важным средством характеристики данных, а также проведения сравнения наборов данных. Одна­ко во многих случаях показатели средней недостаточны для проведения прием­лемого различия между разными распределениями. Рассмотрим простой пример сравнения понедельной заработной платы всех работников двух предприятий (табл. 10).

Т а б л и ц а 10

Средняя заработная плата рабочих двух предприятий

Предположим, что все другие показатели идентичны, то есть предприятия одинаковы по размеру, условиям работы и предоставляемым по­собиям и льготам. Также следует отметить, что для получения средней на осно­вании двух наборов данных по заработной плате использовался один и тот же метод расчета, в соответствии с которым приведенные значения – средние арифметические. Единственное реальное различие между предприятиями состо­ит в уровне оплаты работников. Из таблицы видно, что средняя заработная плата на предприятии Б несколько выше, чем на предприятии А. Таким обра­зом, при наличии выбора на основании данной информации многие из нас предпочли бы пойти работать на предприятие Б. Вместе с тем средние не дают нам всей картины в целом. Например, для проведения более качественного сравнения было бы полезно выяснить верхнюю и нижнюю планки заработной платы на двух предприятиях. Так, табл. 11 дает в сравнении дополнительную информацию по двум предприятиям.

Т а б л и ц а 11

Характеристика заработной платы рабочих двух предприятий

На основании этой дополнительной информации предприятие А предстается в более благопри­ятном свете: мы видим, что минимальная заработная плата на двух предприя­тиях аналогична, но на предприятии А гораздо выше максимальная заработная плата. Таким образом, хотя для многих работников предприятия Б средний уровень заработной платы выше, чем на предприятии А, на последнем значи­тельно выше потенциал в том, что касается заработной платы. Все работники предприятия Б получают одинаковую заработную плату. Это означает, что прак­тически отсутствуют условия для роста работника и стимулы к такого рода росту минимальны. Напротив, на предприятии А имеется существенный резерв для роста. Диапазон заработной платы здесь значительно шире, что свидетель­ствует о существенном разбросе в уровне оплаты различных категорий работни­ков, иначе говоря, в данной организации имеется существенный стимул для тех, кто ставит перед собой высокие цели. С учетом данной информации процесс выбора между двумя предприятиями становится более сложным. Наиболее амбициозные работники предпочтут работать на предприятии А, а низкоопла­чиваемые работники – на предприятии Б.

Данный пример иллюстрирует ситуацию, при которой средние не дают полной картины: помимо показателей среднего значения полезно получить данные по разбросу в двух наборах данных. В данной главе мы рассмотрим некоторые меры разброса, которые можно использовать для этих целей.

Показатели вариации делятся на две группы: абсолютные и от­носительные. К абсолютным относятся размах вариации, сред­нее линейное отклонение, дисперсия и среднее квадратическое отклонение. Вторая группа показателей вычисляется как отноше­ние абсолютных показателей вариации к средней величине. Относительными показателями вариации яв­ляются коэффициенты осцилляции, вариации, относительное линейное отклонение и др.

Рассмотрим расчет основных показателей вариации для характеристики предприятий по стоимости ОФ (табл.12), средняя стоимость ОФ () = 6 тыс. у. е.

I. Абсолютные показатели вариации.

1. Размах вариации (R) характеризует разность между наибольшим (Xmax) и наи­меньшим (Xmin) значениями варьирующего признака:

, (15)

Для нашего примера: R = 13 – 1 = 12 тыс. у. е.

Разброс значений стоимости ОФ для данных предприятий составляет 12 тыс. у. е.

Т а б л и ц а 12

Характеристика предприятий по стоимости основных фондов

2. Среднее линейное отклонение (d). Оно вычисляется как средняя арифметическая из абсолютных значений отклонений вариант xi и (взвешенная или простая в зависимости от исходных условий), по след. формулам:

, (16)

(простая средняя)

, (17)

(взвешенная средняя)

Поскольку сумма отклонений значений признака от средней величины равна нулю, приходится все отклонения брать по модулю.

d =240/100 =2,4 тыс. руб. Размер ОФ данных предприятий отклоняется по абсолютной величине от средней стоимости фондов (6 тыс. руб) в средней на 2,4 тыс. руб.

3. Дисперсия и среднее квадратическое отклонение.

Дисперсия () представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины и вычисляется по формулам простой и взвешенной дисперсии (в зависимости от исходных данных). Дисперсия есть средняя величина квадратов отклонений.

, (18)

(простая дисперсия)

, (19)

(взвешенная дисперсия)

Дисперсия является базой расчета показателя – среднего квадратического отклонения.

Среднее линейное отклонение () равно корню квадратному из дисперсии:

, (20)

или

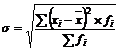, (21)

Среднее квадратическое отклонение – это обобщающая характеристика размеров вариации признака в совокупности и показывает, как в среднем значения xi отклоняются в ту и другую сторону от найденной средней. Оно выражается в тех же единицах, что и признак (в метрах, тоннах, рублях, процентах и т. д.).

тыс. у. е. Размер основных фондов данных предприятий отклоняется от среднего размера 6 тыс. руб в ту и другую сторону в среднем на 2,9 тыс руб.

II. Относительные показатели вариации:

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15