-  площадь между кривой и осью ot равна единице, как интег­рал Пуассона;

-  если случайная величина представляет сумму двух независи­мых случайных величин, следующих каждая нормальному закону, то она тоже следует нормальному закону.

Объективная характеристика соответствия эмпирического распределения нормальному может быть получена с помощью особых статистических показателей – критериев согласия. Известны критерии согласия К. Пирсона, , и .

4.3. Структурные характеристики вариационного ряда распределения

Кроме рассмотренных средних величин в качестве статистических характеристик вариационных рядов распределения рассчитываются так называемые структурные средние – мода и медиана.

Мода (Мо) представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой. Медианой (Ме) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.

Пример 1. Имеются данные о заработной плате рабочих бригады (у. е.):

500, 450, 300, 440, 440, 560, 440, 470, 460

Найдем моду и медиану:

1) т. к. наиболее часто встречается заработная плата, равная 440 у. е., то Мо = 440 у. е.;

2) для определения медианы необходимо упорядочить данные:

300, 440, 440, 440, 450, 460, 470, 500, 560

450 у. е. – середина ранжированного ряда, то есть Ме = 450 у. е.

Если ранжированный ряд включает четное число единиц, то медиана определяется как средняя из двух центральных значений.

Пример 2 . Имеются данные о распределении рабочих предприятия по тарифному разряду:

Определение моды по дискретному вариационному ряду не со­ставляет большого труда – наибольшую частоту (60 человек) име­ет 5-й тарифный разряд, следовательно, он и является модальным.

Для определения медианного значения признака по следующей формуле находят номер медианной единицы ряда (Nмe):

, (28)

где п – объем совокупности.

Полученное дробное значение, всегда имеющее место при чет­ном числе единиц в совокупности, указывает, что точная середи­на находится между 95-м и 96-м рабочими. Необходимо опреде­лить, к какой группе относятся рабочие с этими порядковыми но­мерами. Это можно сделать, рассчитав накопленные частоты. Очевидно, что рабочих с этими номерами нет в первой группе, где всего лишь 12 человек, нет их и во второй группе (12+48=60). 95-й и 96-й рабочие находятся в третьей группе (12+48+56=116), следовательно, медианным является 4-й тарифный разряд.

В отличие от дискретных вариационных рядов определение моды и медианы по интервальным рядам требует проведения оп­ределенных расчетов на основе соответствующих формул.

Сравнение средних

Три метода получения средней равнозначны. В зависимости от цели исследования распределения долж­на выбираться одна из упомянутых характеристик, либо же для сравнения – все три.

Средняя арифметическая широко распространена (очевидна для большинства людей). Для нее характерно то, что все от­клонения от нее (положительные и отрицательные) в сумме рав­няются нулю. Основной недостаток: среднее может быть искажено экстремальными значениями.

Мода отражает типичный, наиболее распространенный (часто встречающийся) вариант значения признака. Недостаток: не подходит для нестандартного распределения, т. е. включающего 2 и более максимума.

Медиана практически выполняет функции средней для неоднородной, не подчиняющейся нормаль­ному закону распределения совокупности.

Проиллюстрируем ее познавательное значение следующим примером.

Допустим, нам необходимо дать характеристику среднего дохо­да группы людей, насчитывающей 100 человек, из которых 99 име­ют доходы в интервале от 100 до 1000 долл. в месяц, а месячные доходы последнего составляют 50 000 долл.:

Если мы воспользуемся средней арифметической, то получим средний доход, равный примерно 600–700 долл., который не только в несколько раз меньше дохода 100-го человека, но и имеет мало общего с доходами остальной части группы. Медиана же, равная в данном случае 163 долл., позволит дать объективную характе­ристику уровня доходов 99 % данной группы людей.

Соотношение моды, медианы и средней арифметической ука­зывает на характер распределения признака в совокупности, по­зволяет оценить его асимметрию.

В симметричных распределениях все три характеристики совпа­дают. Чем больше расхождение между модой и средней арифме­тической, тем больше асимметричен ряд.

Рассмотрим диаграмму распределения заработной платы рабочих (рис.10).

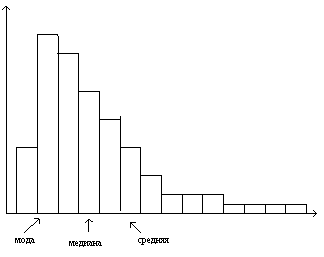Рис.10. Распределение доходов

Данная диаграмма иллюстрирует типичное распределение доходов всех работников крупной организации. Это положительно асимметрич­ное распределение, с областью больших отклонений в правой части диаграммы. Доходы основной массы работников представлены в левой части диаграммы. Только несколько работников имеют доходы, представленные у верхней грани­цы диаграммы. Вот эти-то несколько работников и искажают значение средней, и «усредненное» значение, полученное путем расчета арифметической сред­ней, превышает приемлемо репрезентативное значение. Значение моды соот­ветствует максимальному значению частот, представленных в распределении. При такой форме распределения это значение находится в области нижних значений заработной платы и поэтому также не является полностью репрезен­тативным. Значение медианы, как центральное значение, выступает в роли компромиссного решения и часто считается наилучшим показателем.

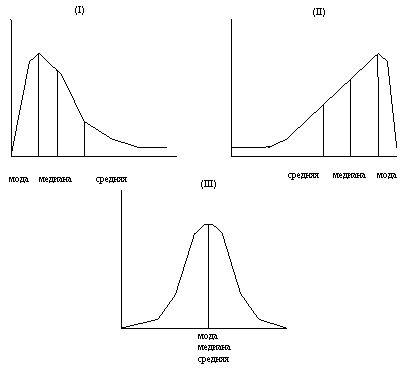Рис. 11. Сравнение распределений

На рис.11 представлены три типа распределения с соответствующими показателями трех «средних»: значения средней, моды и медианы. Эти три показателя будут находиться в соответствии друг с другом, только если распределение данных симметрично. Если распределение отрицательно асимметрично, тогда последовательность значений меняется на обратную (ii). Так, средняя будет наи­меньшим значением, а мода – наибольшим.

5. ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ

5.1. Выборочное наблюдение как важнейший источник статистической информации

Выборочное наблюдение ставит перед собой задачу – по обследуемой части дать характеристику всей совокупности единиц при условии соблюдения всех правил и принципов проведения статистического наблюдения и научно организованной работы по отбору единиц.

В настоящее время популярность выборочного исследования возросла. На современном этапе появилось множество субъек­тов хозяйственной деятельности, которые характерны для рыноч­ной экономики. Речь идет об акционерных обществах, малых и совместных предприятиях, фермерских хозяйствах и т. д. Сплош­ное обследование этих статистических совокупностей, состоящих из десятков и сотен тысяч единиц, потребовало бы огромных ма­териальных, финансовых и иных затрат. Использование же выбо­рочного обследования позволяет значительно сэкономить силы и средства, что имеет немаловажное значение.

Наряду с экономией ресурсов одной из причин превращения выборочного наблюдения в важнейший источник статистической информации является возможность значительно ускорить получе­ние необходимых данных. Ведь при обследовании, скажем, 10 % единиц совокупности будет затрачено гораздо меньше времени, а результаты могут быть представлены быстрее и будут более акту­альными. Фактор времени важен для статистического исследования особенно в условиях изменяющейся социально-экономичес­кой ситуации.

Роль выборочного обследования в получении статистических дан­ных возрастает в силу возможности – когда это необходимо – рас­ширения программы наблюдения. Так как исследованию подверга­ется сравнительно небольшая часть всей совокупности, можно бо­лее широко и детально изучить отдельные единицы и их группы.

Проведение статистического наблюдения вообще требует соот­ветствую-щего кадрового обеспечения. Сплошное обследование занимает иногда слишком большое число людей для его органи­зации проведения. Обращение же к опыту выборочного наблюде­ния приводит к тому, что необходимый штат сотрудников значитель­но уменьшается. Это позволяет привлекать более квалифициро­ванных людей, снизить опасность появления субъективных оши­бок, особенно при непосредственной регистрации фактов, и достичь поставленных целей с помощью меньшего количества бо­лее компетентных специалистов-статистиков.

Совокупность отобранных для обследования единиц в статистике принято называть выборочной, а совокупность единиц, из кото­рых производится отбор, – генеральной.

Основные характеристики генеральной и выбороч­ной совокупностей обозначаются определенными символами (табл. 13).

Т а б л и ц а 13

Характеристики генеральной и выборочной совокупностей

п р о д о л ж е н и е т а б л и ц ы 13

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15