Проектирование магнитных систем электротехнических устройств (стр. 9 )

Создание объемов через «выдавливания» плоскости.

1. Main Menu > Preprocessor > Modeling > Operate > Extrude > Areas > By XYZ Offset

С помощью курсора сначала выбирается поверхность 1 моделирующая полюсной наконечник. После подтверждения выбора в появившемся окне Extrude Areas by XYZ Offset (рисунок 3.75) указывается направление и дистанция «выдавливания». Исходя из условий задачи (таблица 3.1, рисунок 3.40) в строке Offsets for extrusion в ячейку соответствующую параметру DZ (вдоль оси 0Z) необходимо ввести половину длины полюсного наконечника lпн/2 = - 32,5 мм.

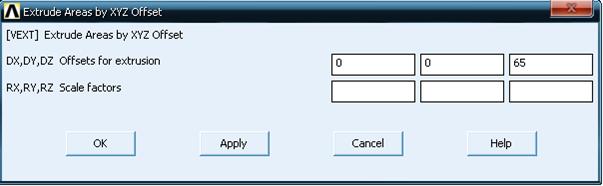
Рисунок 3.75 – Окно ввода дистанций «выдавливания» поверхностей

Те же манипуляции следует выполнить с поверхностью 2, но дистанция «выдавливания» должна соответствовать половине толщины магнитопровода Tмп/2 = - 12,5 мм.

Команда:

VEXT, NA1, NA2, Ninc, DX, DY, DZ, RX, RY, RZ

где NA1, NA2 – номер начальной и конечной поверхности;

Ninc – шаг, через который высчитывается номер следующей поверхности;

DX, DY, DZ – расстояние, на которое происходит смещение компонента, вдоль выбранной оси;

RX, RY, RZ – масштабные коэффициенты, применяемые к координатам точек при выполнении операции.

Пример использования команды:

vext,1,,,,,-32.5

vext,2,,,,,-12.5

Результат 3

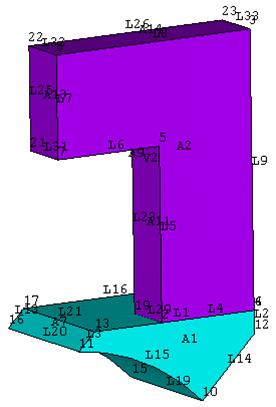
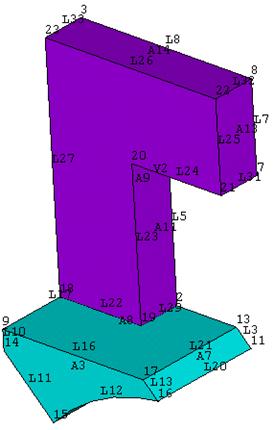
С помощью окна Pan-Zoom-Rotate можно убедиться в выполнении действия.

Далее следует создать сечение трубопровода, который представляет собой 1/8 часть полого цилиндра с толщиной стенки 4 мм. Строить данную геометрию удобней методом «сверху-вниз».

2. Main Menu > Preprocessor > Modeling > Create > Volumes > Cylinder > By Dimentions

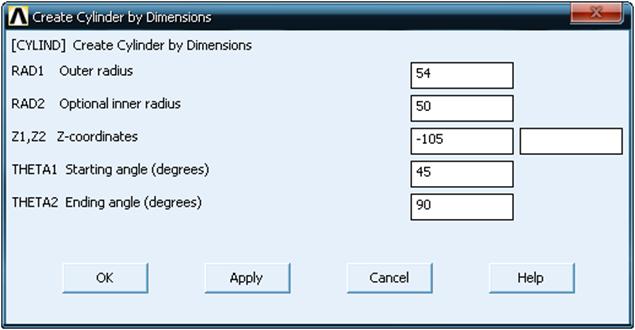
Рисунок 3.76 – Окно ввода геометрических размеров части

полого цилиндра

Посредством данного пункта, построение ведется от центра активной системы координат. В появившемся окне Create Cylinder by Dimensions (рисунок 3.76) следует ввести значение: внешнего радиуса Outer radius Rпн = 54 мм, внутреннего радиуса Optional inner radius rв = 50 мм, длины отрезка трубопровода Z-coordinates Lтр = - 105 мм, начальный и конечные углы Starting angle 45°, Ending angle 90° [24].

Команда:

CYLIND, RAD1, RAD2, Z1, Z2, THETA1, THETA2

где RAD1, RAD2 – внешний и внутренний радиус создаваемого цилиндра;

Z1, Z2 – координаты торцевых граней цилиндра по оси 0Z;

THETA1, THETA2 – начальный и конечный угол создаваемого цилиндрического сектора.

Пример использования команды:

cylind,54,50,-105,,45,90

Результат 4

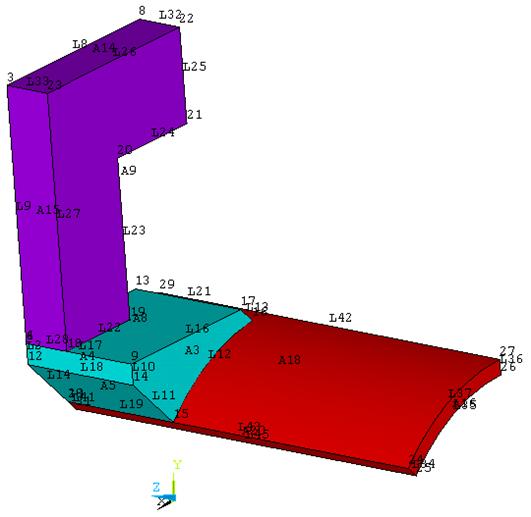
Полость трубопровода можно заполнить несколькими (3) частями:

-  Область, которая находится непосредственно под полюсным наконечником. Метод построения такой же, как и при моделировании трубопровода, со значением внешнего R = 50 мм и внутреннего радиуса rв = 0 мм, дистанция «выдавливания» равна половине длины полюсного наконечника (lпн/2) в отрицательном направлении оси 0Z.

-  Граница – пяти миллиметровая область от края рабочей зоны. Граничная область строится «выдавливанием» из поверхности 22, в отрицательном направлении оси 0Z на дистанцию 5 мм.

-  Область, заполняющая остальную полость трубопровода, получается путем «выдавливания» из поверхности 27 в отрицательном направлении оси 0Z на расстояние 67,5 мм.

Пример использования команд:

cylind,50,,-lpn/2,,45,90

vext,22,,,,,-5*msht

vext,27,,,,,-100+lpn/2

Результат 5

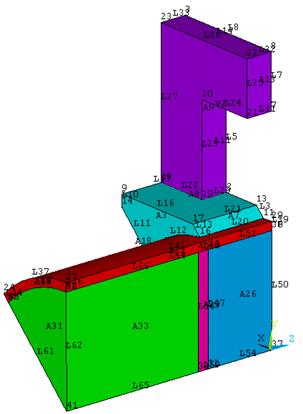
Перед созданием геометрии окружающего воздушного пространства необходимо построить дугу через точки 11 и 29 радиусом Rтр = 54 мм.

Модель окружающего модуль воздуха состоит из двух частей, одна представляет собой параллелепипед, а вторая имеет сложную геометрическую форму.

Создание параллелепипеда.

3. Main Menu > Preprocessor > Modeling > Create > Volumes > Block > By Dimensions

В окне Create Block by Dimensions в соответствующие ячейки необходимо ввести координаты начала и конца ребра по осям (рисунок 3.77).

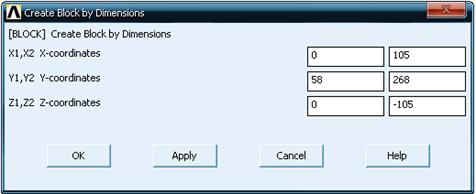
Рисунок 3.77 – Окно ввода координат вершин создаваемого параллелепипеда

В результате будет построен куб размером 105 х 210 х 105 мм начинающийся у верхней поверхности полюсных наконечников и поглощающий весь магнитопровод.

Команда:

BLOCK, X1, X2, Y1, Y2, Z1, Z2

где X1, X2 – ввод координат угловых точек куба по оси 0X;

Y1, Y2 – ввод координат угловых точек куба по оси 0Y;

Z1, Z2 – ввод координат угловых точек куба по оси 0Z;

Пример использования команды:

block,0,105,58,268,0,-105

Результат 6

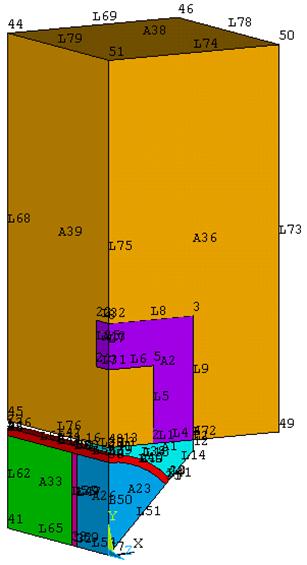
Для создания второй части модели окружающего воздуха нужно создать точку 52 с координатами (105, 38.2, 105). Далее через точки 52, 49, 48, 29, 11, 10 построить плоскость 41, создав из нее объем, с помощью операции «выдавливания» длиной, равной отрезку трубопровода.

Результат 7

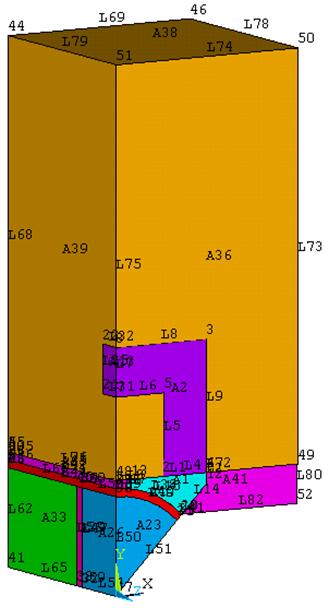
Объемы 7 и 8 можно объединить.

Объединение объемов.

4. Main Menu > Preprocessor > Modeling > Operate > Booleans > Add > Volumes

С помощью курсора «мыши» выбираются объемы (7 и 8), которые необходимо объединить. После подтверждения выбора произойдет слияние двух компонент в новый объем 9.

Созданная геометрическая модель на данном этапе не адекватна. Также как и при построении двумерной модели необходимо провести «булевские» операции по перекрытию пересекающихся и «склеиванию» (сопряжению) соприкасающихся объемов.

Перекрытие одного объема другим.

5. Main Menu > Preprocessor > Modeling > Operate > Booleans > Overlap > Volumes

С помощью курсора необходимо указать объемы 1, 2 и 9 модели и подтвердить выбор. К пересекающимся объемам будет применено действие «перекрытие». Результатом действия станет появление новых объемов 7, 8 и 10 вместо 1, 2 и 9 соответственно.

Команда:

VOVLAP, NV1, NV2, NV3, NV4, NV5, NV6, NV7, NV8, NV9

где NV1…NV9 – номера перекрывающихся объемов.

Пример использования команды:

vovlap,1,2,9

Результат 8

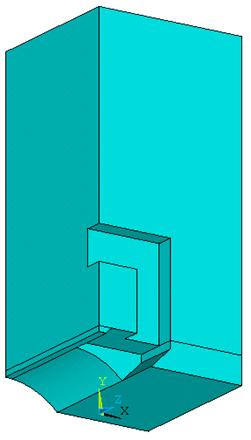
Сопряжение соприкасающихся объемов.

6. Main Menu > Preprocessor > Modeling > Operate > Booleans > Glue > Volumes

С помощью курсора необходимо указать все объемы и подтвердить выбор. После данного действия необходимо упорядочить номера всех компонентов. Упорядочивание номеров идентично пункту 14 раздела 3.2.6.

Выбор конечного элемента для анализа модели

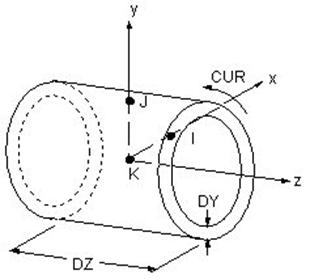
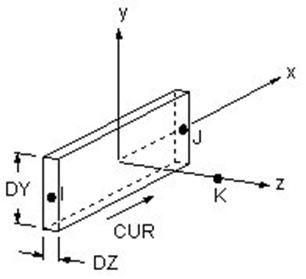
Описать трехмерную геометрическую модель можно при помощи сетки трехмерных конечных элементов. Для решения магнитостатической задачи необходимы элементы со степенью свободы, позволяющей рассчитать скалярный магнитный потенциал. В библиотеке ANSYS имеется 3 типа конечных элементов пригодных для решения подобных задач: вырожденный линейный – SOLID96 и квадратичный (параболический) – SOLID98 (рисунок 3.78). Сравнение параметров этих элементов приведены в таблице 3.3 и 3.4 [1]

Таблица 3.3 – Сравнение характеристик элементов

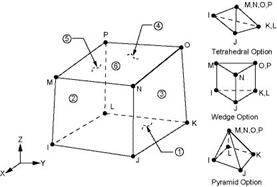
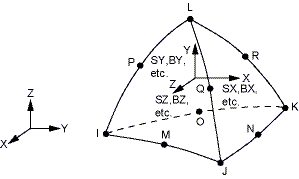
а) б)

Рисунок 3.78 – а) Восьми узловой конечный элемент SOLID96;

б) Десяти узловой конечный элемент SOLID98

Таблица 3.4 – Возможные выходные результаты

Примечание: фраза «по составляющим» означает, что вектор величины раскладывается на составляющие по осям.

Как видно из таблицы 3.4 конечный элемент SOLID98 имеет более широкий спектр решаемых задач, позволяет точно описывать сложные, нелинейные формы.

Элемент SOLID96 позволяет решать только задачи магнитостатики и магнитодинамики, подготовка его к расчету скалярного магнитного потенциала не требует специальных настроек, может вырождаться в различные формы, а это, при определенной оптимизации построения сетки, позволяет более точно описывать геометрическую область [1].

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23