[M][u] = [v]. (2.10)
Заметим, что вид матрицы [М] зависит только от пространственного распределения узлов поля, но не зависит от того, является ли поле лапласовым или пуассоновым.
В отношении решения этих уравнений следует отметить две важные особенности. Во-первых, в любой практической задаче число уравнений очень велико (цифра 1 000 является вполне обычной) и, во-вторых, число членов в каждом из уравнений очень мало. Первая из этих особенностей приводит к тому, что обычные методы нахождения точных решений становятся совершенно неприемлемыми просто в связи с чрезмерной длительностью вычислений. Так, например, для решения 100 уравнений методом исключения переменных (который гораздо быстрее метода определителей) потребуется, по крайней мере, 10 000 ч при выполнении расчетов вручную, поэтому необходимо использовать компьютерную технику. Однако, к счастью, благодаря малому числу членов в уравнениях можно применить два значительно более быстрых численных метода. Это тесно связанные релаксационный и итерационный методы, основанные на процессе последовательных приближений. В качестве характеристики быстроты этих методов можно указать, что 100 уравнений в конечных разностях могут быть решены с точностью 0,1 % примерно за 8 часов вручную (релаксационным методом) и примерно за 1 мин при использовании вычислительной машины (итерационным методом). Дополнительное преимущество этих методов состоит в том, что продолжительность расчетов тесно связана с получаемой точностью, поэтому можно прервать расчет, когда будет достигнута требуемая точность.
Релаксационный метод решения совместных уравнений в конечных разностях был впервые применен Гауссом, однако его чрезвычайные универсальность и действенность не были оценены инженерами и физиками до 30–40-х годов 19-го столетия, когда он был повторно открыт и усовершенствован Саусвеллом и его сотрудниками. В основном он сводится к непрерывному изменению значений потенциала, продолжающемуся до тех пор, пока все совместные уравнения не будут удовлетворены с достаточной степенью точности. Этот метод предназначен для расчетов вручную и эффективность применения его зависит от опыта расчетчика. В последнем отношении он существенно отличается от других методов, рассмотренных, поскольку невозможно сформулировать общие правила выполнения операций и при решении какой-либо конкретной задачи два расчетчика никогда не будут точно следовать по одному и тому же пути. В связи с этим определения основных операций решения, приведенные ниже, на первый взгляд могут показаться недостаточно полными. Однако ввиду крайней простоты метода уже небольшая практика быстро дает опыт, необходимый для выбора правильного пути решения любой задачи.
2.2.1 Релаксационный метод
В основе релаксационного метода лежит понятие об остатке. Если потенциалы А0, A1, ..., А4 выбраны таким образом, что уравнение в конечных разностях (2.8) справедливо, то его правая часть равна нулю. Однако, если значения потенциалов не удовлетворяют этому уравнению, то его правая часть равна не нулю, а некоторой величине R0, определяемой соотношением
![]() (2.11)
(2.11)
Величина R0 называется остатком уравнения в конечных разностях для узла 0, и релаксационный метод заключается в последовательном уменьшении до нуля (снятии) остатков всех уравнений. Если остатки всех уравнений в конечных разностях равны нулю, то значения потенциала соответствуют точному решению, однако практически для получения хорошего приближения к точному решению достаточно ограничиться уменьшением их до малых значений.
Следует отметить, что строгой зависимости между величинами остатков и точностью определения потенциалов не существует. Однако практикой установлено, что решения в общем случае удовлетворительны, если:
а) значения отдельных остатков уменьшены примерно до 0,1% среднего значения потенциалов;
б) алгебраическая сумма всех остатков имеет тот же порядок, что и отдельные остатки;
в) распределение остатков с учетом их величины и знаков равномерно по всей области поля.
Более подробно релаксационный метод описан в [7].
Релаксационный метод рассчитан главным образом на выполнение расчетов вручную и в этом отношении обладает двумя характерными особенностями.
а) Метод вызывает интерес у расчетчика, постоянно требуя изобретательности и сноровки.
б) Сущность метода такова, что исправление ошибок происходит автоматически (в ходе выполнения обычных операций); поэтому он не требует систематической проверки.
Исходя из предшествующего анализа, можно прийти к выводу о невозможности составления твердых правил, которые могли бы быть использованы при решении любой конкретной задачи, и в действительности именно этой универсальностью в основном объясняется действенность метода в руках опытного расчетчика. Точно так же отсутствие твердых правил препятствует успешному программированию метода для расчета на вычислительной машине.
Однако можно дать ряд полезных практических рекомендаций:
Размер ячейки сетки. Одно из основных требований касается правильного определения размера ячейки сетки; при этом для уменьшения неудобств, связанных с появлением асимметричных звезд, выбор должен быть сделан таким образом, чтобы сетка на возможно большем участке совпадала с границей. На первых этапах расчета не следует использовать мелкую сетку, поскольку это связано с непроизводительной затратой труда и приводит к медленной сходимости. Напротив, первый расчет должен быть выполнен с помощью крупной сетки, а когда для нее будет получена удовлетворительная сходимость, следует перейти к более мелкой сетке. Размер ячейки новой сетки удобно принять равным половине размера ячейки предыдущей сетки; тогда новые узлы будут расположены посредине между старыми. Значения потенциала новых узлов находятся с удовлетворительным приближением в результате линейной интерполяции (поскольку она дает точность, эквивалентную точности уравнений в конечных разностях). Последовательное уменьшение размера ячейки сетки должно производиться до тех пор, пока не будет получена достаточно мелкая сетка.
Применение мелких сеток, конечно, должно быть ограничено небольшими областями, для которых точность расчета особенно важна.
Составление расчетного формуляра. После выбора наиболее рационального размера ячейки сетки необходимо вычертить границу (и сетку) в таком масштабе, чтобы было достаточно места для выполнения расчетов на сетке. Целесообразно выполнять чертеж на плотной бумаге, а расчеты производить на накладываемых на него листах кальки; это позволяет сохранить чертеж при стирании записей резинкой.
Десятичные дроби. Десятичные дроби вообще не рекомендуется использовать при расчетах, поскольку они неудобны и увеличивают опасность появления ошибок. Вместо этого при необходимости (например, если десятичные дроби присутствуют в исходных данных, при уменьшении остатков до значений порядка единицы или переходе к более мелкой сетке) все числа следует умножить на 10 в соответствующей степени и выполнять расчеты в целых цифрах. Единственное исключение из этого правила может быть допущено на последних этапах расчета для узлов, связанных с асимметричными звездами. Изменения остатка в асимметричных звездах, вообще говоря, связаны с появлением десятичных дробей. Но даже для таких звезд на первых этапах расчета вполне достаточно учитывать лишь целые числа, округляя числа, содержащие десятичные дроби. Это оправдано, благодаря тому что погрешности в определении остатков (возникающие в результате округления) легко могут быть исправлены на любом этапе расчета путем пересчета остатков, исходя из текущих значений потенциала.
Расчет. Как было показано выше, задача расчета заключается в том, чтобы сделать остатки и их алгебраическую сумму малыми величинами и распределить их равномерно между узлами сетки. Следует по возможности шире применять блочную (или линейную) релаксацию и переходить к узловой релаксации лишь тогда, когда дальнейшее составление блоков становится нецелесообразным. В первую очередь должно быть обращено внимание на области, где остатки особенно велики, а также на области, где они окружены остатками противоположного знака, поскольку в таких случаях как положительные, так и отрицательные остатки могут быть сняты одновременно.
Проверка. Выше уже отмечалось, что возникающие в ходе расчетов ошибки в основном исправляются автоматически, однако их следует свести к минимуму внимательными вычислениями, поскольку они замедляют сходимость. Для того чтобы получить уверенность в отсутствии расхождения между значениями потенциала и остатка в узлах (приводящего к ошибке в определении потенциала, если остатки равны нулю), в ходе расчета важно время от времени, особенно при переходе к более мелкой сетке, производить пересчет остатков, исходя из текущих значений потенциала.
2.2.2 Итерационный метод
При решении уравнений в конечных разностях итерационным методом, так же как и при использовании релаксационного метода, производится непрерывное изменение значений потенциала до тех пор, пока все уравнения не будут удовлетворены с достаточной степенью точности. Положения относительно устойчивости и точности решения для обоих методов аналогичны, однако все итерационные методы характеризуются двумя особенностями, которые отличают их от релаксационного метода.
Во-первых, они разработаны для использования в полностью автоматическом цикле операций, где каждое из уравнений (и, следовательно, каждый узел сетки) рассматривается в ходе расчетов по очереди. Во-вторых, уточненные значения потенциала находятся непосредственно из уравнений в конечных разностях и понятие об остатке в этом отношении не используется. Первая из отмеченных выше особенностей проявляется, в том, что основной итерационный метод имеет более медленную сходимость, чем релаксационный метод. Однако она в то же время позволяет легко запрограммировать итерационные методы для расчетов на вычислительной машине и, таким образом, исключает необходимость выполнения вручную расчетов, которые при использовании релаксационного метода могут быть очень трудоемкими.
Возможность применения вычислительных машин является большим преимуществом данного метода, и, действительно, повышение интереса к итерационным методам тесно связано с развитием компьютерной техники. За последнее время было предпринято интенсивное исследование этой проблемы со стороны математиков, что привело к непрерывному созданию и совершенствованию действенных методов. Однако наилучшим из них с точки зрения общего применения для решения практических задач в настоящее время является так называемый экстраполяционный метод Либмана, сочетающий быструю сходимость и простоту.
Так же как и для релаксационного метода, можно привести несколько общих указаний относительно применения метода. Ряд рекомендаций, основанных на анализе и опыте, изложен ниже.
а) Число итераций, требуемых для получения заданного снижения ошибки, возрастает примерно пропорционально квадратному корню из числа узлов.
б) Наилучшая сходимость характерна для «простых» конфигуральных границ, таких, как квадрат, и ухудшается для более сложных областей, особенно имеющих узкие зоны
в) При заданных конфигурации границ и числе узлов сходимость для краевых задач второго и третьего рода хуже, чем для краевых задач первого рода.
г) При использовании сильно завышенного значения α зависимость изменения остатка в функции числа итераций становится колебательной.
д) Если задание начального распределения потенциалов имеет существенное значение для более продолжительных расчетов, то для коротких расчетов, лучше произвести дополнительные итерации и не тратить время на выполнение ориентировочного расчета и подготовку данных для вычислительной машины.
Необходимо так же упомянуть об использовании для получения быстрой сходимости изменяющегося в ходе итерационного процесса коэффициента сходимости. Хотя определение оптимального значения α на каждом этапе расчета очень сложно даже методом повторных попыток, предложен ряд вполне удовлетворительных расчетных схем, в которых используются переменные, хотя и не обязательно оптимальные значения а. В одной из них, α принимает значения 1 и 2, причем 1 используется в тех случаях, когда соседние остатки имеют противоположные знаки, а 2, когда они имеют одинаковые знаки.
2.2.3 Граничные условия для градиента
Уравнения в конечных разностях, которые будут выведены ниже, одинаково пригодны для релаксационного и итерационного методов.
Подлежащие рассмотрению граничные условия относятся к прямолинейным и криволинейным границам, совпадающим и не совпадающим с узлами сетки, и к поверхностям раздела между областями, которые в общем случае имеют различные электрические или магнитные постоянные и разные значения плотности тока. Существует очень много различных комбинаций, перечисленных выше факторов, и нет необходимости детально рассматривать уравнения в конечных разностях для каждого случая. Однако рассмотрим наиболее важные уравнения, полученные в общем виде.
Границы делятся на две группы в зависимости от того, совпадают ли они с узлами сетки или нет. Границы, совпадающие с узлами, параллельные линиям сетки и диагональные по отношению к ним, границы, не совпадающие с узлами, параллельные линиям сетки (но не совпадающие с ними), а также общий случай криволинейных границ.
2.2.4 Границы, совпадающие с узлами сетки
Для каждой из двух разновидностей границ, совпадающих с узлами сетки, а именно параллельных и диагональных по отношению к сетке, требуются два разных уравнения в конечных разностях: одно – для узлов, расположенных в углах границы, а другое – для остальных узлов, лежащих на границе. Для той или другой разновидностей границ вначале рассмотрены узлы, не примыкающие к углам, а анализ параллельных границ предшествует анализу диагональных границ.
Наиболее общие условия на границе или поверхности раздела, которые могут встретиться в практике, относятся к двум областям, имеющим различные магнитные проницаемости, при протекании в одной из них тока, и эти условия приняты для каждой из описанных выше разновидностей границ. Для особенно полезного случая параллельных границ представлен также ряд важных частных модификаций уравнений.
Границы, параллельные линиям сетки; общий случай. Рассмотрим границу и узлы, изображенные на рисунке 2.13. Допустим, что в области а, лежащей слева от границы, протекает ток, распределенный равномерно с плотностью J, а область б, лежащая справа от границы, обесточена. Кроме того, предположим, что индекс а определяет величины А, μ и W в области а, а индекс б относится к тем же величинам в области б.
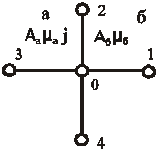
Рисунок 2.13 – Граница параллельная линиям сетки
Для всех узлов в области а, включая лежащие на границе, удовлетворяется уравнение Пуассона, поэтому согласно уравнению (2.8) для узла 0 имеем:
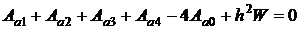 (2.12)
(2.12)
а для всех узлов в области б справедливо уравнение Лапласа, в связи с чем из (2.8) при W = 0 для узла 0
следует:
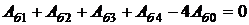 (2.13)
(2.13)
Однако потенциалы Аа1 и Аб3 не имеют физического смысла, поскольку узлы 1 и 3 лежат соответственно в областях а и б. Такие потенциалы называются фиктивными и часто применяются при анализе влияния границ. Хотя они и не используются практически, тем не менее их можно рассматривать как математические величины, необходимые для вывода уравнения, относящегося к узлу, лежащему на границе. Это объясняется тем, что в граничные условия между двумя областями, выраженные в конечных разностях, также войдут фиктивные величины Аа1 и Аб3 и их, таким образом, можно исключить с помощью уравнений (2.12) и (2.13).
В окончательном виде уравнение в конечных разностях для типового узла 0 будет иметь вид
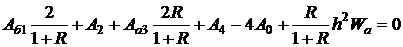 (2.14)
(2.14)
Граница между областями полей Пуассона и Лапласа; одинаковые магнитные проницаемости. Часто применяется уравнение для узлов, лежащих на границе между областями, имеющими одинаковые магнитные проницаемости, когда в одной из них протекает ток, а в другой тока нет. Его нетрудно получить, положив в уравнении (2.14) ![]() , т. е. R=1, откуда
, т. е. R=1, откуда
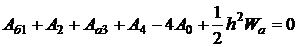 (2.15)
(2.15)
Граница между двумя областями полей Лапласа; различные магнитные проницаемости. Уравнение для узла, лежащего на границе между двумя областями, свободными от токов, с различными магнитными проницаемостями можно получить, положив в уравнении (2.14) Wa = 0. В этом случае может потребоваться также уравнение для скалярного потенциала.
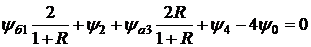 (2.16)
(2.16)
где 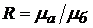 для магнитных полей и
для магнитных полей и ![]() для электрических полей.
для электрических полей.
Если R = 1, то уравнение (2.16) превращается в простое уравнение Лапласа в конечных разностях для симметричной звезды.
Граница между двумя областями полей Лапласа; магнитная проницаемость одной из них бесконечно велика. Если магнитная проницаемость области а бесконечно велика, то поток пересекает границу под прямым углом. Это условие для нормальной составляющей градиента выражается уравнением
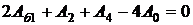 (2.17)
(2.17)
которое нетрудно получить, положив в уравнении (2.14) R = 0.
Угловой узел для границ, параллельных сетке; общий случай. Приведенные выше уравнения относятся ко всем узлам, за исключением узлов, лежащих в углах границы; для таких углов требуется другое уравнение. Рассмотрим прямой угол, образуемый поверхностью раздела между областями а и б, имеющими те же магнитные проницаемости и токи, что и прежде (рисунок 2.14). В связи с представлением поля дискретными точками действительная конфигурация границ не поддается точному учету и для вывода уравнения, относящегося к угловому узлу, необходимо ввести две дополнительные границы.
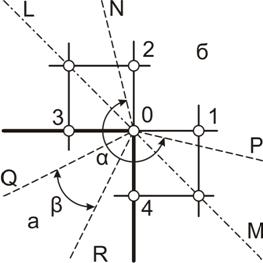
Рисунок 2.14 – Угловой узел для границ
Они расположены симметрично по отношению к углу и представлены пунктирными линиями, образующими углы α и β. Для узла 0, лежащего на границе N0Р, действительно одно и то же уравнение при любом значении α в пределах ![]() и аналогичным образом одно (но другое) уравнение справедливо для того же узла, лежащего на границе Q0R, при любом значении β в пределах
и аналогичным образом одно (но другое) уравнение справедливо для того же узла, лежащего на границе Q0R, при любом значении β в пределах ![]() . Исходя из этих двух уравнений, находим уравнение для узла 0, лежащего на действительной границе, которое дает среднее из двух значений А0.
. Исходя из этих двух уравнений, находим уравнение для узла 0, лежащего на действительной границе, которое дает среднее из двух значений А0.
Уравнение для границы Q0R нетрудно получить на основании анализа случая, когда β=0 (при этом граница исчезает); оно имеет вид:
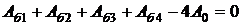 (2.18)
(2.18)
В то же время уравнение для границы NOP в частном случае, когда ![]() , соответствует уравнению для границы LM. Уравнение в конечных разностях для узлов, лежащих на такой диагональной границе, представлено следующим образом:
, соответствует уравнению для границы LM. Уравнение в конечных разностях для узлов, лежащих на такой диагональной границе, представлено следующим образом:
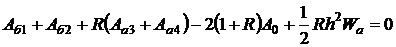 (2.19)
(2.19)
Следовательно, объединив уравнения (2.18) и (2.19) и принимая во внимание равенство Аа3 и Аб3, а также Аа4 и Аб4, получим уравнение для узла 0, расположенного в вершине прямого угла поверхности раздела, в виде:
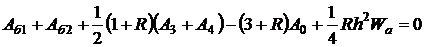 (2.20)
(2.20)
Соответствующие уравнения для случая, когда ток протекает в области б, находятся таким же путем.
Важный частный случай, вытекающий из уравнения (2.20), относится к узлу, расположенному в вершине угла области с бесконечно большой магнитной проницаемостью, занимающей три квадранта (т. е. образующей угол ![]() ), когда обе области обесточены. Результирующее уравнение для случая, когда область б имеет бесконечно большую магнитную проницаемость, можно получить, положив в приведенном выше уравнении
), когда обе области обесточены. Результирующее уравнение для случая, когда область б имеет бесконечно большую магнитную проницаемость, можно получить, положив в приведенном выше уравнении 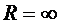 . Тогда
. Тогда
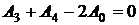 (2.21)
(2.21)
Границы, диагональные по отношению к сетке; общий случай.
При выводе уравнений для узлов, лежащих на границе, диагональной по отношению к сетке (рисунок 2.15), возможны два подхода, которые приводят к уравнениям, связывающим различные группы узлов. Можно или непосредственно использовать с небольшими изменениями уравнения, полученные выше, или составить новую (и более точную) систему уравнений.
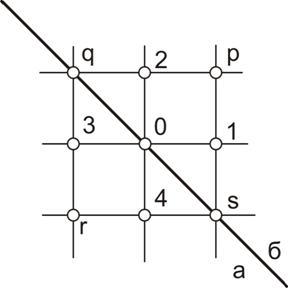
Рисунок 2.15 – Диагональная граница по отношению к сетке
Для того чтобы применить выведенные выше уравнения к диагональной границе, необходимо повернуть звезду в лежащем на границе узле на 45° и увеличить размер ячейки сетки в ![]() раз. Таким образом, с использованием обозначений на рисунке 2.15 общее уравнение, полученное из уравнения (2.14), будет иметь вид:
раз. Таким образом, с использованием обозначений на рисунке 2.15 общее уравнение, полученное из уравнения (2.14), будет иметь вид:
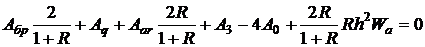 (2.22)
(2.22)
В связи с укрупнением сетки это уравнение менее точно, чем уравнения для узлов, не лежащих на границе.
Более точное уравнение для узла 0 можно получить, исходя из значений потенциала в узлах 1–4, по методу, аналогичному использованному при выводе уравнения (2.14); при этом необходимо рассмотреть узлы х и у, где х является средней точкой отрезка, соединяющего узлы 1 и 2, а у – средней точкой отрезка, соединяющего узлы 3 и 4. Потенциал А0 в узле 0 удовлетворяет уравнениям Пуассона и Лапласа в конечно-разностном виде. Выполнив некоторые преобразования приходим к уравнению в конечных разностях в виде:
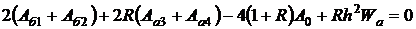 (2.23)
(2.23)
Угловой узел в случае диагональных границ; общий случай.
Уравнение для узла, лежащего в вершине прямого угла, образованного пересечением двух поверхностей раздела, диагональных по отношению к сетке, можно получить из предпосылок, аналогичных использованным выше. Если область а, где протекает ток, представляет собой квадрант, в котором находится узел 3, то уравнение будет иметь вид:
 (2.24)
(2.24)
2.2.5 Границы, не совпадающие с узлами сетки
Теперь перейдем к рассмотрению общей группы границ, не совпадающих с узлами сетки (включая как прямолинейные, так и криволинейные границы). Однако прежде чем приступить к общему анализу, остановимся на частном случае прямолинейной границы, параллельной линиям сетки (но не совпадающей с ними).
Прямолинейная граница, параллельная сетке. При анализе этой группы границ вводятся дополнительные узлы в точках пересечения границы с сеткой (рисунок 2.16).
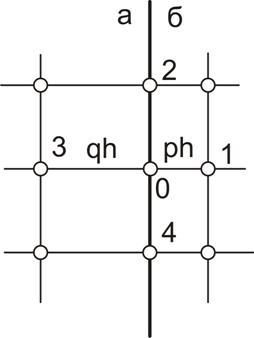
Рисунок 2.16 – Прямолинейная граница параллельная сетке
Уравнение Пуассона в конечных разностях для любого из таких дополнительных узлов имеет вид:
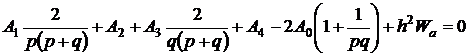 (2.25)
(2.25)
Используя это уравнение для определения фиктивных потенциалов Аа1 и Аб3 и подставив найденные выражения в уравнение (2.14), отражающее граничные условия, получим уравнение в конечных разностях для узлов, лежащих на границе, в виде:
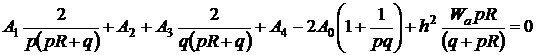 (2.26)
(2.26)
Оно выведено в обычном предположении, что ток протекает только в области а. При использовании этого уравнения узлы на границе рассматриваются непосредственно как часть общей сетки. Это, конечно, приводит к необходимости применения уравнений в конечных разностях для асимметричных звезд, которые относятся к узлам, расположенным на границе и в непосредственной близости к ней.
Криволинейные границы; общий случай.
Ряд уравнений составлен для использования в случае криволинейных границ, вдоль которых задана нормальная составляющая градиента, однако, насколько нам известно, не было предложено общего уравнения, связывающего поля по ту и другую стороны границы, соответствующего уравнению (2.14). Если бы такие уравнения существовали, то их применение было бы связано со многими трудностями: они были бы очень громоздкими, расчеты были бы связаны с многочисленными измерениями длин отрезков для асимметричных звезд и необходимыми геометрическими построениями; кроме того, для получения достаточно точных результатов потребовалась бы очень мелкая сетка. Поэтому наиболее правильным выходом из положения является не применение дополнительных уравнений в конечных разностях, а аппроксимация конфигурации границы большим числом прямолинейных участков, параллельных или диагональных по отношению к линиям сетки. Точность такого представления можно оценить, исходя из рассмотрения отклонений принятой конфигурации границ от действительной.
В связи с изложенными выше замечаниями, а также ввиду того, что наиболее общий тип граничных условий в практике встречается редко, можно отказаться от попытки вывести общие уравнения и сосредоточить внимание на частном случае граничных условий для нормальной составляющей градиента, которые встречаются наиболее часто.
Граничные условия для нормальной составляющей градиента.
Рассмотрим криволинейную границу, изображенную на рисунке 2.17, вдоль которой задано распределение нормальной составляющей градиента ![]() .
.
Рисунок 2.17 – Криволинейная граница
Простейший подход заключается во введении дополнительных узлов, таких, как F, по другую сторону границы и нахождении фиктивных значений потенциала в этих узлах (например, AF) с использованием обычных уравнений для реальных узлов. Потенциал АF можно найти с помощью одного из нескольких несложных геометрических построений. Простое и дающее хорошие результаты построение, заключается в следующем. Проводим прямую FH, перпендикулярную границе и пересекающую ее в точке G. Далее, находим на ней точку Р из условия PG = FG и проводим через точки L и Р прямую до пересечения с отрезком MN в точке Q. Таким образом, потенциалы точек F и Р связаны соотношением
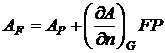
AP находится линейной интерполяцией, исходя из значений AL и AQ a AQ определяется путем линейной интерполяции по АM и AN; отсюда
 (2.27)
(2.27)
То же выражение (и построение) относится, конечно, ко всем участкам границы. Уравнение (2.27) используется главным образом для важного случая, когда тангенциальная составляющая поля равна нулю; при этом ![]() и AF = AP.
и AF = AP.
Методы конечных разностей могут быть использованы для решения любой задачи по определению статического двухмерного поля (и даже трехмерных и неустановившихся полей). Следует отметить, что, несмотря на сравнительную простоту задач, они не поддаются решению с помощью аналитических методов. Решения, найденные методом конечных разностей, являются приближенными, однако можно получить любую желаемую степень точности при условии, если расчет продолжается достаточное время. Тем не менее, для многих практических задач требуемую точность удается получить очень быстро. Необходимо считаться с тем, что все численные методы требуют отдельного решения для каждой совокупности параметров задачи (хотя в некоторых случаях можно значительно сократить время расчетов, приняв конечное решение одной задачи в качестве исходных данных для другой аналогичной задачи). Если задача может быть решена как аналитическими, так и численными методами, то выбор часто определяется продолжительностью расчетов. Конечно аналитические методы обычно являются предпочтительными, однако в некоторых приложениях они могут потребовать настолько длительной обработки, а иногда и расчетов, что численные методы станут более экономичными. Это особенно вероятно в том случае, если для итерационного метода подготовлена общая программа расчета на вычислительной машине и требуется лишь ввести данные, определяющие конфигурацию границ и граничные условия.
Выбор между релаксационным и итерационным методами в основном зависит от того, будут ли расчеты проводиться вручную или на вычислительной машине, а также от задаваемой точности решения, числа подлежащих расчету частных случаев и граничных условии задачи. Для решений, требующих высокой точности, или при большом объеме расчетов преимущества итерационного метода несомненны, однако для некоторых задач с очень сложными конфигурацией границ и граничными условиями ценность этого метода ограничена двумя обстоятельствами. Во-первых, число узлов сетки и вспомогательных величин, необходимых для правильной формулировки задачи, может быть ограничено объемом памяти вычислительной машины и, во-вторых, может потребоваться слишком много времени для составления программы. В том и другом случаях в настоящее время, особенно для задач, в которых на криволинейных границах задаются условия для градиента, предпочтительны методы расчета вручную. Однако задачи Дирихле для всех конфигураций границ и задачи, в которых на прямолинейных границах задана нормальная составляющая градиента, нетрудно решить итерационными методами с использованием разработанных для них общих программ.
2.3 МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
Метод конечных элементов (МКЭ) на основе вариационного принципа возник из решения задач теории упругости, что и определило, в основном, терминологию, используемую в процессе его применения в других разделах механики сплошных сред (теории теплопроводности, газовой динамике и др.) [9]. Использование в МКЭ методов взвешенных невязок (таких, например, как методы коллокаций Галеркина, наименьших квадратов) позволило отказаться от вариационного принципа в МКЭ, тем более что не для всякой задачи можно построить функционал, минимум которого дает исследуемое дифференциальное уравнение. Тем самым круг решаемых задач механики сплошных сред был существенно расширен [22, 23, 25].
Пусть в области 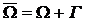 необходимо решить некоторую дифференциальную задачу. Тогда в МКЭ осуществляется следующая цепочка процедур.
необходимо решить некоторую дифференциальную задачу. Тогда в МКЭ осуществляется следующая цепочка процедур.
1. Область ![]() разбивают на подобласти в количестве Е штук (
разбивают на подобласти в количестве Е штук (![]() ), называемые конечными элементами, такие что
), называемые конечными элементами, такие что
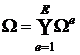 ,
, 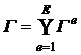 .
.
2. В каждом конечном элементе ![]() выбирается система нумерованных узлов, в которых значения искомой функции являются неизвестными величинами.
выбирается система нумерованных узлов, в которых значения искомой функции являются неизвестными величинами.
3. Каждому нумерованному узлу приписывается базисная функция такая, что в этом узле она равна единице, а в остальных нумерованных узлах расчетной области – нулю. Число базисных функций в расчетной области равно числу нумерованных узлов, причем для различных узлов они обладают свойством линейной независимости (или ортогональности) по всей расчетной области.
4. Решение искомой дифференциальной задачи приближенно строится в виде линейной комбинации базисных функций по всем нумерованным узлам расчетной области с коэффициентами линейной комбинации, равными значениям искомой функции в нумерованных узлах.
5. Это решение подставляется в дифференциальную задачу, и, поскольку решение приближенное, результатом подстановки будет не тождественный нуль, а некоторая функциональная невязка.
6. С помощью известных методов взвешенных невязок (коллокаций, Галеркина, наименьших квадратов) функциональная невязка минимизируется по всей расчетной области путем приравнивания нулю скалярного произведения функциональной невязки и весовых функций (скалярное произведение от непрерывных функций равно определенному интегралу по расчетной области от произведения этих функций), причем в методе взвешенных невязок Галеркина весовые функции в нумерованных узлах совпадают с базисными функциями. В результате получается система линейных алгебраических уравнений (СЛАУ) относительно значений искомой функции в нумерованных узлах, коэффициентами в которой являются интегралы по всей расчетной области от базисных функций и их производных.
7. Определенные интегралы по всей расчетной области заменяются на сумму интегралов по конечным элементам, что, в силу ортогональности базисных функций, делает матрицу СЛАУ сильно разреженной, с ненулевыми элементами, расположенными в окрестности главной диагонали (так называемые ленточные матрицы, частным видом которых является трехдиагональная матрица).
8. Решается СЛАУ относительно узловых значений искомой функции каким-либо известным методом (Гаусса, простых итераций, Зейделя и т. п.). Результаты решения подставляются в приближенное решение по п. 4. При этом полученные значения искомой функции в нумерованных узлах каждого конечного элемента могут быть использованы для получения решения во всех точках конечного элемента ![]() с помощью так называемых функций элементов, простейшим случаем которых является линейный интерполяционный многочлен в
с помощью так называемых функций элементов, простейшим случаем которых является линейный интерполяционный многочлен в ![]() согласно [23].
согласно [23].

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |




