Проектирование магнитных систем электротехнических устройств (стр. 2 )

Для характеристики электромагнитных полей в материальных средах отличных от свободного пространства (вакуума) введенных векторов и недостаточно.

Сила взаимодействия зарядов, а значит и напряженности электрического поля зависят от характера среды, в которой происходит взаимодействие. Влияние вещества среды на электрическое поле вызывается поляризацией вещества под действием поля. При этом молекулы вещества, обладающие собственным дипольным моментом и хаотически ориентированные в отсутствие внешнего электрического поля, приобретают под его воздействием упорядоченную ориентацию, создавая собственное электрическое поле, а свободные заряды начинают двигаться направленно (см. рисунок 1.2).

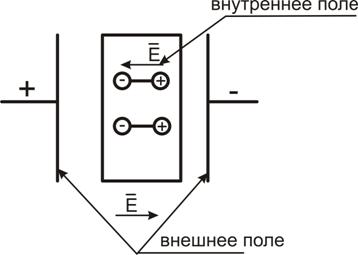
Рисунок 1.2 – Поляризация вещества

Для описания электрического поля в средах вводится вектор электрической индукции :

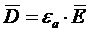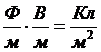, () (1.4)

где 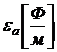 – абсолютная диэлектрическая проницаемость среды.

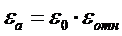, (1.6)

где  – диэлектрическая проницаемость вакуума, в системе СИ 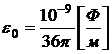, то в вакууме:

, (1.7)

в среде

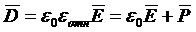, (1.8)

где  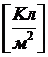– поляризованность вещества

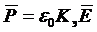, (1.9)

где  – диэлектрическая восприимчивость (безразмерный коэффициент, характеризующий среду).

Основное достоинство вектора заключается в его независимости от параметров среды. Действительно, если амплитуда напряженности поля точечного заряда , находящегося в среде с диэлектрической проницаемостью на расстоянии от заряда, определяется выражением

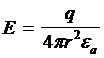, (1.10)

то амплитуда вектора электрической индукции на основании (1.4) определяется только величиной этого заряда

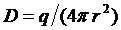. (1.11)

В общем случае, когда поле создается не одним точечным зарядом, а совокупностью произвольно расположенных зарядов, вектор будет определяться величинами и взаимным расположением зарядов относительно точки наблюдения. Таким образом, введение вектора упрощает описание электромагнитных полей в веществе и позволяет получить соотношения для любых сред, независимо от их электромагнитных свойств.

При воздействии магнитного поля на движущийся заряд (или проводник с током) величина вектора также зависит от свойств среды. Эта зависимость объясняется намагничиванием вещества, в результате которого на внешнее магнитное поле накладывается дополнительное поле вещества. При этом в зависимости от свойств вещества возможно, как ослабление первичного магнитного поля в диамагнитных средах, так и усиление в парамагнитных, особенно в ферромагнитных средах.

Рисунок 1.3 иллюстрирует процесс намагничивания вещества.

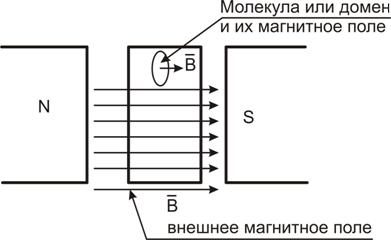
Рисунок 1.3 – Намагничивание вещества

Для описания магнитного поля в различных средах, вводится вектор  – напряженности магнитного поля:

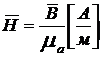, (1.12)

где 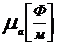 – абсолютная магнитная проницаемость среды характеризует взаимодействие магнитного поля и среды.

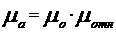, (1.13)

где  – абсолютная магнитная проницаемость вакуума в СИ .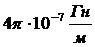

т. о. в вакууме

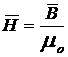. (1.14)

в среде:

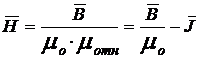, (1.15)

где  – намагниченность вещества.

Таким образом, электромагнитное поле в любой среде полностью характеризуется векторными величинами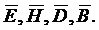

Следует также отметить, что они были введены в результате обобщения большого числа экспериментальных данных, выражением которых являются основные законы электромагнитного поля (закон Кулона, закон Фарадея и др.).

1.3 ЭЛЕКТРОМАГНИТНЫЕ ПАРАМЕТРЫ

И КЛАССИФИКАЦИЯ СРЕД

Диэлектрическая и магнитная проницаемость совместно с удельной проводимостью дают полную характеристику электрических свойств среды. Два первых параметра рассмотрены выше и, соответственно, определяют способность среды поляризоваться при воздействии электрического поля () и намагничиваться при воздействии внешнего магнитного поля (). Третий входит в уравнение, характеризующее воздействие электрического поля на свободные заряженные частицы вещества, под действием которого последние приобретают ориентированное движение, т. е. имеет место ток проводимости [21]. Плотность этого тока и определяется указанным уравнением, представляющим собой закон Ома в дифференциальной форме:

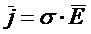, (1.16)

где  – вектор плотности электрического тока, ;

 – удельная электрическая проводимость, .

Таким образом, характеризует степень электропроводимости среды.

В зависимости от свойств параметров , и среды подразделяют на линейные, у которых эти параметры не зависят от величины электрического и магнитного полей, и нелинейные, у которых , и (или хотя бы один из них) зависят от величин электрического и магнитного полей. Практически все реальные среды являются нелинейными, однако, нелинейность проявляется лишь в очень сильных полях, создаваемых в специальных установках.

В дальнейшем будем рассматривать только линейные среды, которые в свою очередь делятся, на однородные и неоднородные, изотропные и анизотропные [16].

Однородными называются среды, параметры которых не зависят от координат и одинаковы во всех точках рассматриваемой среды.

Неоднородные - среды, у которых хотя бы один из параметров , или является функцией координат.

Изотропные - среды, свойства которых не зависят от направления. Для изотропных сред параметры ,, являются скалярными величинами, а векторы и ; и ; и всегда параллельны и связаны между собой соотношениями (1.7), (1.12), (1.16).

Анизотропными называются среды, свойства которых (хотя бы по одному из параметров ,,) различны в различных направлениях.

В анизотропных средах векторы и , и , и могут не совпадать по направлению. Параметры таких сред (или хотя бы один из них) являются тензорными величинами, определяемыми соответствующей матрицей

;

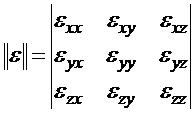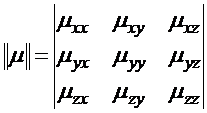; (1.17)

.

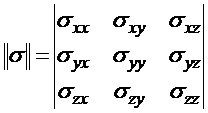Тогда связь между векторами поля будет определяться как

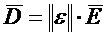; ; . (1.18)

Проводящие свойства среды в переменных полях, кроме проводимости (), зависят также и от частоты колебаний (). В связи с этим среды подразделяются на диэлектрические, полупроводниковые и проводящие, последние будут подробно рассмотрены далее.

1.4 УРАВНЕНИЯ МАКСВЕЛЛА В ИНТЕГРАЛЬНОЙ И

ДИФФЕРЕНЦИАЛЬНОЙ ФОРМАХ

Все электромагнитные процессы макроскопической электродинамики подчиняются законам впервые формализованным (представленным в виде уравнений) выдающимся физиком ХIX столетия Джеймсом Клерком Максвеллом 1Максвелл впервые решил фундаментальную задачу, обобщив имеющиеся экспериментальные закономерности на произвольное электромагнитное поле в произвольной среде. (1864).

Определить электромагнитное поле в некоторой области пространства - значит найти распределение и величины вектора при известных параметрах среды и создающих это поле источниках.

Первое уравнение Максвелла в интегральной форме является обобщением закона полного тока (закона Ампера) связывающего циркуляцию вектора напряженности магнитного поля по любому замкнутому контуру с током проводимости и переменным электрическим полем пронизывающими этот контур (рисунок 1.4).

Первое (1.19) уравнение Максвелла в интегральной форме

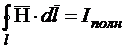, (1.19)

где  – полный ток;

 – ток проводимости;

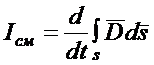 – ток смещения (так как в случае постоянства во времени и пространстве поверхности интегрирования операции дифференцирования и интегрирования можно менять местами, а – на

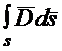 – поток вектора электрической индукции через любую поверхность , опирающуюся на контур , - плотность тока смещения.

Выражение (1.19) читается так: циркуляция вектора напряженности магнитного поля по замкнутому контуру равна сумме тока проводимости и производной по времени от потока вектора электрической индукции через поверхность , ограниченную данным контуром.

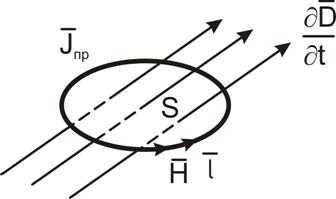
Рисунок 1.4 – К определению первого уравнения Максвелла

Из первого уравнения Максвелла в интегральной форме следует, циркуляция вектора напряженности магнитного поля вдоль замкнутого контура определяется полным током равным сумме тока проводимости тока смещения через поверхность ,ограниченную данным контуром (рисунок 1.4)

Физический смысл первого уравнения Максвелла: вихревое магнитное поле возбуждается током проводимости, и изменяющимся во времени электрическим полем.

Применим теорему Стокса

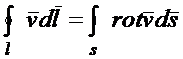(1.20)

где  – циркуляция векторного поля;

 – замкнутая кривая ограничивающая поверхность S;

 – проекция на внешнюю нормаль к поверхности.

к левой части уравнения (1.19)

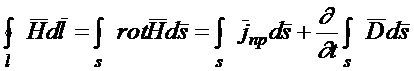, т. к. (1.21)

поверхность S выбирается произвольно - подынтегральные выражения одинаковы

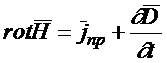(1.22)

получаем первое уравнение Максвелла в дифференциальной форме.

Уравнение Максвелла в дифференциальной форме определяет взаимосвязь между векторами поля в каждой точке пространства.

Второе уравнение Максвелла в интегральной форме является обобщением закона электромагнитной индукции, открытого Фарадеем, и связывающим наводимую в замкнутом проводящем контуре ЭДС с изменяющимся во времени магнитным потоком, пронизывающим этот контур (рисунок 1.5).

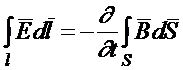(1.23)

Это второе уравнение Максвелла в интегральной форме читается так: циркуляция вектора напряженности электрического поля по любому замкнутому контуру , определяется скоростью изменения потока вектора магнитной индукции через поверхность ограниченную данным контуром

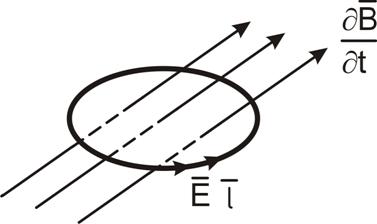
Рисунок 1.5 – К определению второго уравнения Максвелла

Физический смысл: изменяющееся во времени магнитное поле вызывает появление вихревого электрического поля .

Аналогично, используя теорему Стокса:

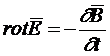(1.24)

получаем второе уравнение Максвелла в дифференциальной форме

Физический смысл – если в некоторой точке 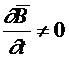,то в этой точке существует вихревое электрическое поле.

Знак «минус» следует из правила Ленца, гласящем, что индуктивный ток в контуре имеет всегда такое направление, при котором создаваемый им собственный поток сквозь поверхность, ограниченную контуром препятствует изменению магнитного потока , вызывающего появления индуктивного тока.

Третье уравнение Максвелла в интегральной форме, является обобщением закона Гаусса, который, как известно, получен экспериментально и связывает поток вектора электрического смещения через произвольную замкнутую поверхность с зарядом , сосредоточенным внутри этой поверхности (рисунок 1.6).

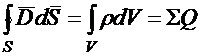(1.25)

это третье уравнение Максвелла в интегральной форме, где  – плотность объемного заряда.

Или : 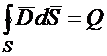, (1.26)

где заряд может быть произвольным образом распределен внутри поверхности , ограничивающей некоторый объем (рисунок 1.6).

Уравнение (1.25) читается так: поток вектора электрической индукции через замкнутую поверхность равен суммарному электрическому заряду внутри этой поверхности.

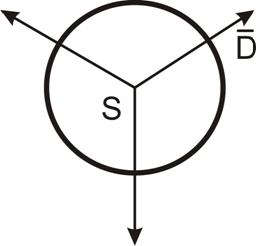
Рисунок 1.6 – К определению третьего уравнения Максвелла

Физический смысл – если существуют заряды - они возбуждают потенциальное электрическое поле.

Применяя теорему Остроградского-Гаусса

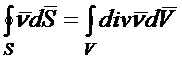(1.27)

к левой части уравнения (1.25) и приравнивая подынтегральное выражение, получаем третье уравнения Максвелла в дифференциальной форме:

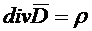(1.28)

Физический смысл – источник вектора - свободные заряды.

Закон Гаусса строго доказывается только для электростатических полей. Максвелл постулировал его справедливость для произвольных сред, любых зарядов и полей, как угодно изменяющихся во времени и пространстве.

Четвертое уравнение Максвелла в интегральной форме совпадает с законом Гаусса для магнитного поля, согласно которому, поток вектора через любую замкнутую поверхность равен нулю (рисунок 1.7).

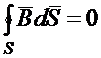(1.29)

это четвертое уравнение Максвелла в интегральной форме.

Равенство нуля потока вектора через любую замкнутую поверхность показывает, что линии вектора непрерывны и не имеют ни начала, ни конца. Они либо замкнуты, либо уходят в бесконечность.

Физический смысл – в природе отсутствуют магнитные заряды.

Уравнение (1.29) читается так: поток вектора магнитной индукции через замкнутую поверхность равен нулю.

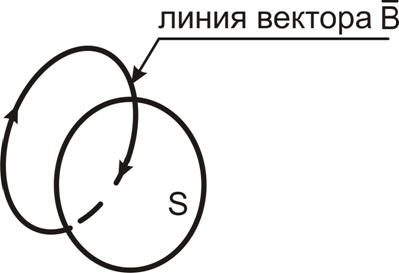
Рисунок 1.7 – К определению четвертого уравнения Максвелла

Используя теорему Остроградского-Гаусса получаем четвертое уравнение Максвелла в дифференциальной форме

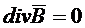(1.30)

Для того чтобы облегчить определение поля внутри областей, обтекаемых токами, вводят векторный магнитный потенциал , который определяется из условия, чтобы его интеграл по любому замкнутому пути был равен полному потоку, охватываемому этим путем. Если площадь охватываемой путем поверхности, стремиться к нулю, то предельное значение интеграла, отнесенное к единице площади, равно магнитной индукции . Следовательно,

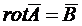(1.31)

Вектор лежит в плоскости, перпендикулярной направлению вектора . Уравнение 1.31 определяет только производную , а для полного определения векторного потенциала необходимо также знать его дивергенцию.

Для любого рассматриваемого двумерного поля вектор расположен в плоскости, перпендикулярной направлению потока, и следовательно, параллелен направлению тока. Отсюда, поскольку изменение между двумя магнитными линиями равно потоку между этими линиями на единицу длины в направлении тока, обладает свойствами функции потока, а линии, соединяющие точки с одинаковыми значениями , являются магнитными линиями.

1.5 УРАВНЕНИЯ МАКСВЕЛЛА В КОМПЛЕКСНОЙ ФОРМЕ

Все реальные электромагнитные процессы можно представить либо в виде суммы дискретных гармонических колебаний либо в виде непрерывного спектра гармонических колебаний, поэтому изучение гармонических во времени электромагнитных полей представляет большой практический и теоретический интерес. Такие поля часто называют монохроматическими. В буквальном переводе монохроматический, означает одноцветный. Название взято из оптики: как известно, каждому цвету соответствуют колебаниям определенной частоты.

При исследовании процессов, гармонически изменяющихся во времени, весьма удобным математическим аппаратом является, символический метод или метод комплексных амплитуд, известных из теории электрических цепей [17]. Согласно его, любой гармонически изменяющейся функции

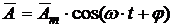, (1.32)

где Аm – амплитуда;

j – начальная фаза;

;

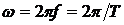f и T – частота и период гармонического колебания.

можно поставить в соответствие комплексный вектор

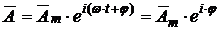, (1.33)

где 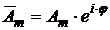 – не зависящий от времени комплексный вектор, модуль и аргумент которого, являясь функциями пространственных координат и показывают как изменяются в пространстве амплитуда и фаза гармонически изменяющейся величины (по аналогии - комплексная амплитуда скалярной функции А).

Как известно по формуле Эйлера:

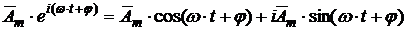, (1.34)

следовательно, для перехода от комплексной амплитуды к мгновенному значению исходной функции нужно вычислить реальную часть .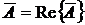

Необходимо отметить, что в общем случае вместо разложения вектора А по ортам декартовой системы координат может оказаться необходимым разложение по каким-либо другим ортогональным векторам, что не вносит в рассмотрение никаких принципиальных изменений. Если функция А удовлетворяет линейным уравнениям, то таким же уравнениям будут удовлетворять соответствующие комплексные функции . Однако определение комплексных функций во многих случаях оказывается проще определения исходных функций.

Уравнения Максвелла являются линейными дифференциальными уравнениями. Поэтому при изучении монохроматических электромагнитных полей можно вместо векторов и рассматривать комплексные векторы и .

И, таким образом, имея запись уравнений Максвелла в форме, позволяющей вычислить комплексные амплитуды вектора и () 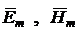легко получить и их мгновенные значения.

Для комплексной записи первого уравнения Максвелла в комплексной форме вычислим производную

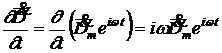. (1.35)

Тогда первое уравнение Максвелла в комплексной форме будет иметь вид

. (1.36)

Используя уравнение связи и закон Ома , а также разделив обе части уравнения на получим

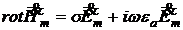
, (1.37)

или после преобразования

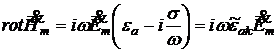, (1.38)

где  – комплексная диэлектрическая проницаемость среды.

Проделав аналогичные преобразования в остальных уравнениях, получим систему уравнений Максвелла в комплексной форме

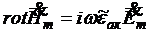
(1.39)

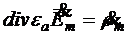
Следует иметь ввиду то, что возможность использования в данном случае метода комплексных амплитуд обусловлена линейностью уравнений Максвелла. Линейность же позволяет использовать этот метод и при анализе сложных негармонических функций. Естественно, при этом предварительно представить данную функцию в виде спектра (дискретного или непрерывного) гармонических функций, с последующим применением принципа суперпозиции.

1.6 КЛАССИФИКАЦИЯ СРЕД ПО ПРОВОДИМОСТИ

Рассмотрим более подробно первое уравнение Максвелла в комплексной форме

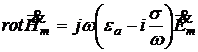(1.40)

очевидно, что сомножитель, стоящий в скобках зависит от параметров среды - диэлектрической проницаемости, проводимости и частоты электрического поля, кроме того, очевидно, что диэлектрическая проницаемость определяет величину плотности тока смещения в среде:

, (1.41)

а проводимость - плотность тока проводимости

(1.42)

Соответственно величина 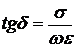определяет отношение плотности тока проводимости к плотности тока смещения в среде с параметрами и на частоте .

При этом в электродинамике принято считать, что в случае:

если 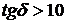среда является проводником – (токи проводимости >> токов смещения);

если 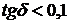– среда является диэлектриком;

если 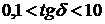– среда полупроводник.

Необходимо обратить внимание, что классификация среды зависит от частоты и при разных частотах одна и та же среда может быть как проводник, так и полупроводник или диэлектриком.

Например: почва: , .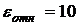

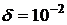f<2 МГц – проводник;

f>200 МГц – диэлектрик;

2<f<200 МГц – полупроводник.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23