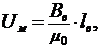1.7 КЛАССИФИКАЦИЯ ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ

Решение уравнений Максвелла является достаточно сложной задачей, однако, для некоторых полей она может быть упрощена, соответственно упрощаются и уравнения Максвелла.

Статическое поле (электростатическое и магнитостатическое) – поле неподвижных, неизменяющихся во времени зарядов ,

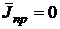
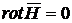
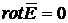
(1.43)

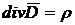
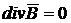
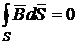
Стационарное поле – поле, создаваемое постоянными токами.

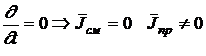
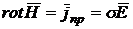
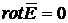
(1.44)

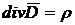
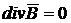
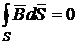
Квазистационарное поле – (медленно изменяющееся во времени)

при этом

если то

; (1.45)

;

.

Быстропеременное поле – описывается полной системой уравнений Максвелла.

2 МЕТОДЫ РАСЧЕТА ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ

2.1 ЦЕПНОЙ МЕТоД

2.1.1 Основные допущения, принимаемые при расчете

магнитных цепей

В современных электрических машинах, трансформаторах, электромагнитных реле, а также в различных измерительных приборах для увеличения магнитного потока используют ферромагнитные сердечники, обладающие большой магнитной проницаемостью по сравнению с проницаемостью воздуха. В связи с этим оказывается возможным сделать некоторые допущения, позволяющие исключить необходимость расчета пространственного распределения характеристик поля.

Перечисленные выше устройства обычно состоят из ферромагнитных сердечников и обмоток, изготавливаемых из изолированных проводников и надеваемых на эти сердечники и образующих ту или иную магнитную цепь [20]. В этом случае расчет магнитной цепи базируется на следующих допущениях.

1. Магнитная проницаемость ферромагнетиков, из которых изготавливаются сердечники магнитной цепи, много больше проницаемости окружающей среды. Это позволяет считать, что с любым витком одной и той же катушки сцеплен один и тот же поток и что на каждом участке магнитной цепи с неизменным поперечным сечением сердечника он остается одним и тем же. А это означает, что в данном случае можно пренебречь потоками рассеяния, замыкающимися как по участкам магнитной цепи, так и в окружающем пространстве.

2. Предполагается, что поперечные размеры ферромагнитных сердечников магнитной цепи малы по сравнению с их длиной. Это позволяет принимать за длину сердечника длину его средней линии, а поле внутри сердечника считать однородным. Тогда падение магнитного напряжения на участке магнитной цепи аб с постоянным сечением можно вычислить следующим образом:

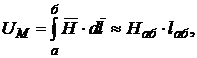
где  - напряженность магнитного поля на участке аб;

 - длина средней линии участка.

3. Предполагается также, что воздушные зазоры между отдельными участками магнитной цепи достаточно малы по сравнению с поперечными размерами сердечников и длиной силовой линии. Это позволяет считать, что в воздушном промежутке магнитное поле остается однородным, а падение магнитного напряжения на нем можно определить следующим образом:

где  - длина воздушного промежутка магнитной цепи;

 - индукция магнитного поля в воздушном зазоре;

 - магнитный поток сердечника;

 - площадь поперечного сечения полюса сердечника;

 - магнитная проницаемость в вакууме.

В магнитных цепях из магнито-мягких материалов зависимость индукции в сердечнике от напряженности магнитного поля принято определять основной кривой намагничивания.

При указанных выше допущениях на основании фундаментального закона магнитостатики - закона полного тока и принципа непрерывности линий вектора индукции магнитного поля получают уравнения для магнитных цепей, аналогичные по форме уравнениям электрических цепей:

а) закон Ома для участка линейной цепи

;

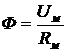б) первый закон Кирхгофа для узлов магнитной цепи

;

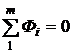в) второй закон Кирхгофа для любого замкнутого контура магнитной цепи

 =  =  = 

где 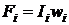 - намагничивающая сила.

Поэтому для расчета магнитных цепей могут быть использованы такие же методы, которые применяются и для расчета электрических цепей.

2.1.2 Расчет неразветвленных магнитных цепей

При расчете неразветвленных магнитных цепей приходится встречаться с двумя видами задач («прямая» и «обратная» задачи).

В «прямой» задаче необходимо определить намагничивающий ток или намагничивающую силу по заданному магнитному потоку, а в «обратной» - поток по заданной величине намагничивающей силы. В обоих случаях, как правило, известны геометрические размеры всех участков магнитной цепи, материалы, из которых они изготовлены, основные кривые намагничивания или петли гистерезиса и числа витков катушек.

Рассмотрим неразветвленную магнитную цепь (рисунок 2.1), состоящую из П-образного сердечника электромагнита и стальной пластины, замыкающей его концы. Между концами сердечника электромагнита и пластиной имеется воздушный зазор . Размеры сердечника электромагнита и пластины, а также материалы, из которых они изготовлены, известны. Необходимо определить намагничивающий ток, при котором магнитный поток в воздушном зазоре имеет заданное значение. Сечение сердечника электромагнита во всех частях одинаково и равно , а сечение пластины - .

При этих условиях всю магнитную цепь представим в виде трех последовательно соединенных участков: сердечника электромагнита, двух воздушных зазоров и стальной пластины с одинаковым потоком . Для расчета магнитной цепи наметим среднюю магнитную линию и определим длины ее отдельных участков , и .

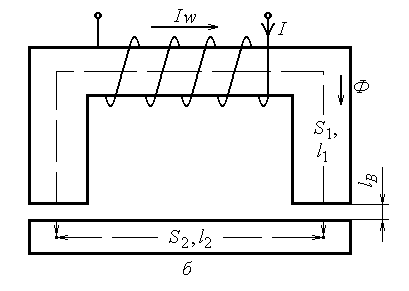
Рисунок 2.1 – Неразветвленная магнитная цепь

Неразветвленную магнитную цепь, изображенную на рисунке 2.1, представим эквивалентной схемой (рисунок 2.2), составленной из трех последовательно соединенных сопротивлений: и и НС 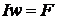. В этой схеме сопротивления и зависят от магнитного потока, а сопротивление является величиной постоянной.

По второму закону Кирхгофа для магнитной цепи намагничивающая сила будет определяться выражением

.

Магнитные индукции определим по заданному значению магнитного потока как

.

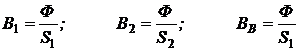По найденным значениям магнитных индукций , и основным кривым намагничивания для соответствующих материалов определим напряженности магнитного поля и .

Для воздушного зазора ,

тогда намагничивающий ток

.

Рассмотрим теперь ту же магнитную цепь (рисунок 2.1), для которой требуется определить магнитный поток по заданному значению намагничивающей силы («обратная» задача). Эта задача в отличие от предыдущей не имеет «прямого» решения вследствие нелинейной связи между потоком и намагничивающим током.

Решение такой задачи можно выполнить, например, следующим методом. Сначала зададимся предполагаемым значением магнитного потока, например , затем, также, как и в предыдущей «прямой» задаче, найдем НС 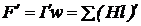. Если полученное значение намагничивающей силы совпадает с заданным, т. е. , то задача решена. Однако такого совпадения после первой попытки обычно не получается. Поэтому следует задаться другими значениями магнитного потока: 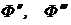и т. д., найти соответствующие значения намагничивающих сил () и т.д. и построить вспомогательную характеристику (рисунок 2.3).

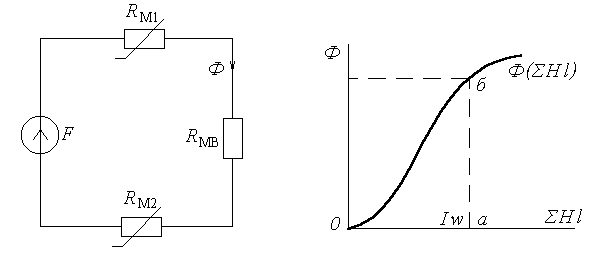
Рисунок 2.2 – Эквивалентная схема Рисунок 2.3 – Вспомогательная

неразветвленной магнитной цепи характеристика

Отложив на оси абсцисс величину заданной намагничивающей силы (рис. 3) получим точку а, проведем из этой точки прямую, параллельную оси ординат, до пересечения с кривой в точке б. В результате получим отрезок а-б, определяющий искомое значение магнитного потока.

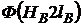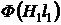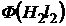Так как магнитный поток во всех участках неразветвленной магнитной цепи один и тот же, то характеристика может быть построена по аналогии с неразветвленной электрической цепью графическим суммированием абсцисс прямой и кривых и для одних и тех же значений магнитного потока.

Характеристика 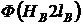 - это прямая, проходящая через начало координат. Ее легко построить, если найти напряженность магнитного поля для какого-нибудь значения :

.

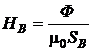Характеристики и 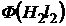строятся при помощи основных кривых намагничивания для материалов первого и второго участков магнитной цепи. Для этого нужно умножить ординаты кривых намагничивания соответственно на сечения первого и второго участков , а абсциссы - на их длины .

2.1.3 Расчет разветвленных магнитных цепей

Расчеты разветвленных магнитных цепей основаны на применении законов Кирхгофа для магнитных цепей. Вследствие нелинейной связи между индукцией и напряженностью магнитного поля расчеты магнитных цепей обычно ведутся графоаналитическими методами аналогично методам расчета нелинейных электрических цепей.

При расчете магнитной цепи, прежде всего, нужно указать на схеме направления намагничивающих сил, если известны направления токов и расположение обмоток, или произвольно выбрать положительные направления намагничивающих сил, если они являются искомыми. Затем необходимо выбрать положительные направления магнитных потоков, после чего можно переходить к составлению эквивалентной схемы и ее расчету.

Пример разветвленной магнитной цепи с одной намагничивающей силой приведен на рисунке 2.4. На рисунке 2.5 показана эквивалентная схема этой магнитной цепи. Для такой магнитной цепи возможен «прямой» расчет, если требуется определить намагничивающую силу по заданному значению потока в воздушном зазоре .

По известному потоку вычислим индукцию

,

по кривой намагничивания найдем напряженность магнитного поля и напряженность поля в воздушном зазоре по формуле

Магнитное напряжение третьей ветви, т. е. между узлами «а» и «б»,

.

Так как вторая и третья ветви соединены параллельно, то и

.

Вычислим 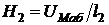, по кривой намагничивания найдем .

Поток Ф2 по формуле

,

а поток Ф1 по формуле

.

Определив поток , вычислим магнитную индукцию

и по кривой намагничивания найдем напряженность магнитного поля .

Тогда по второму закону Кирхгофа искомая намагничивающая сила определится выражением

.

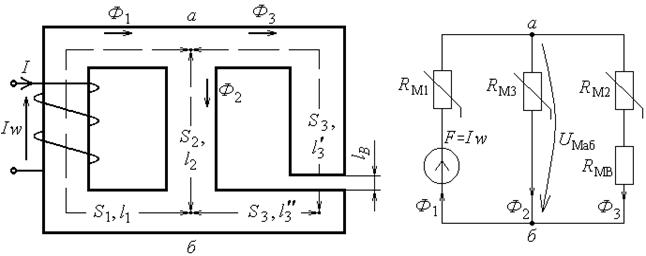
Рисунок 2.4 – Разветвленная Рисунок 2.5 – Эквивалентная схема

магнитная цепь разветвленной магнитной цепи

Рассмотрим порядок решения «обратной» задачи. Необходимо вычислить потоки в ветвях магнитной цепи (рисунок 2.4) по заданной намагничивающей силе. Задача может быть решена графическим методом аналогично расчету цепи постоянного тока с нелинейными элементами.

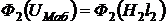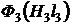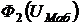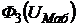Для решения задачи при помощи кривых намагничивания построим кривую (рисунок 2.6) и зависимость путем суммирования ординат прямой и кривой (где ) для одних и тех же значений магнитного потока . Суммированием ординат кривых и для одних и тех же значений магнитного напряжения получим кривую .

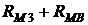Выполненные построения эквивалентны замене двух параллельных ветвей с сопротивлениями и (рисунок 2.5) одним нелинейным сопротивлением, характеристикой которого и является кривая .

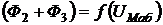Дальнейшие построения для полученной неразветвленной цепи можно выполнить построением характеристики (рисунок 2.6). Точка пересечения кривой с кривой определяет магнитное напряжение между точками а и б и поток . Ординаты точек пересечения и вертикальной прямой 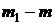с кривым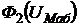и и 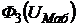дают соответственно потоки и .

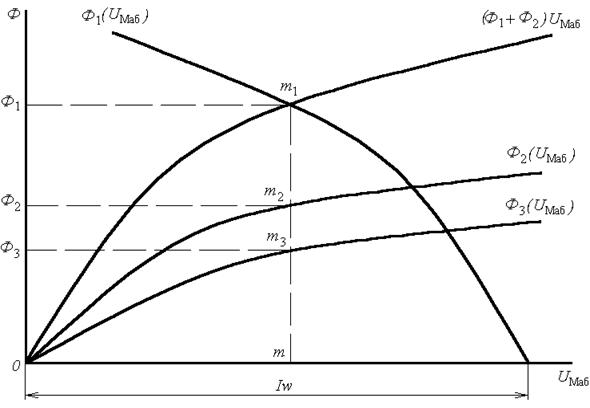
Рисунок 2.6 – Вспомогательная характеристика

2.2 Метод конечных разностей

Методы конечных разностей, которые ведут начало от Гаусса, но получили широкое распространение примерно лишь с 1940 г., могут быть использованы для получения численных решений с любой требуемой степенью точности всех задач при расчете электромагнитных полей. Кроме того, хотя некоторые теоретические обоснования этих методов очень сложны, их практическое применение чрезвычайно просто и фактически сводится к простым арифметическим операциям. Главный недостаток методов конечных разностей заключается в том, что (как и для всех численных методов) решение должно повторяться для каждой совокупности параметров, задаваемых в задаче.

Решения, полученные методом конечных разностей, представляют собой совокупность значений описывающей поле функции в дискретных точках, равномерно распределенных по всей области поля. Эти значения находятся путем замены одного описывающего поле дифференциального уравнения с частными производными системой простых уравнений в конечных разностях, которые имеют вид линейных уравнений, связывающих значение потенциала в каждой точке со значениями потенциала в других точках, окружающих ее. Таким образом, определение поля сводится к решению системы совместных уравнений. В связи с тем, что при решении задачи приходится оперировать с большим числом таких уравнений, применение методов исключения переменных, определителей и обращения матриц становится нецелесообразным. Вместо этого должны использоваться специальные методы. Два наиболее полезных метода, релаксационный и итерационный, тесно связанные, будут рассмотрены далее. Релаксационный метод предназначен для расчетов вручную и является чрезвычайно универсальным, хотя его эффективность зависит от опыта и искусства расчетчика. В противоположность этому другой метод, итерационный, основан на полностью повторяющемся цикле операций и идеально подходит для выполнения расчетов с использованием компьютерной техники, прогресс которой в последние годы значительно содействовал развитию этого метода.

Уравнения в конечных разностях получены применительно к уравнению Пуассона для векторного потенциала; при переходе к уравнению Лапласа плотность тока принимается равной нулю. Естественно, уравнения в конечных разностях имеют одинаковый вид независимо от того, составлены ли они для векторного потенциала А, скалярного потенциала ψ или функции потока j.

При замене уравнения поля системой уравнений в конечных разностях, связывающих значения потенциальной функции в дискретных точках, можно выбрать произвольное пространственное распределение точек. Однако очевидно, что при выборе полностью равномерного распределения точек для каждой из них справедливо уравнение в конечных разностях одного и того же вида и формулировка задачи значительно упрощается. Требуемое распределение обеспечивается расположением точек в «узлах» любой равномерной сетки. Одна такая сетка состоит из квадратов и изображена на рисунке 2.7, для простой, квадратной, области поля. Нетрудно заметить, что положение любого узла, лежащего во внутренней области границы, по отношению к соседним узлам характеризуется приведенной на рисунке 2.8 схемой. Это типовое расположение узлов носит название симметричной звезды.

Рисунок 2.7 – Распределение квадратной равномерной сетки

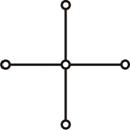
Рисунок 2.8 – Звезда симметричной сетки

Существуют только две другие равномерные сетки: равносторонняя треугольная сетка, изображенная на рисунке 2.9, и правильная шестиугольная сетка, показанная на рисунке 2.10.

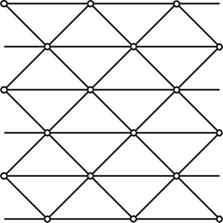
Рисунок 2.9 – Распределение треугольной равномерной сетки

Рисунок 2.10 – Распределение шестиугольной равномерной сетки

Находит применение также неравномерная сетка, представляющая определенный интерес, и полярная сетка. Она имеет очевидные преимущества для некоторых задач с круговыми границами.

Симметричная звезда (рисунок 2.11 б) относится ко всем узлам сетки, за исключением узлов, которые находятся в непосредственной близости к границе, в тех случаях, когда граница и линии сетки не совпадают. Для узла, находящегося в непосредственной близости к такой границе, типовое расположение соседних узлов характеризуется асимметричной звездой, изображенной на рисунке 2.11 а. Уравнение в конечных разностях для потенциала в «центральном» узле 0 отличается от уравнения для центрального узла симметричной звезды, однако поскольку симметричная звезда является частным случаем асимметричной, рассмотрим только асимметричную звезду.

Предположим, что сторона квадрата сетки h, называемая размером ячейки сетки, мала по сравнению с размерами границ, и примем одинаковую нумерацию узлов для обеих звезд, как показано на рисунке 2.11.

а б

Рисунок 2.11 – Звезда асимметричной (а) и симметричной (б) сетки

В случае асимметричной звезды допустим, что узлы 1 и 2 расположены на расстояниях ph и qh от узла 0, где р и q – числа, меньшие единицы. При решении практических задач это означает, что узлы 1 и 2 будут лежать на границе.

Уравнение в конечных разностях получается в результате разложения потенциала узла 0 в ряд Тейлора и нахождения выражений для (д2А/дх2)0 и (д2А/ду2)0, которые вводятся в уравнение Пуассона.

Значение потенциала А в любой точке х, лежащей на линии, проведенной через узел 0 параллельно оси х, может быть выражено через значение потенциала узла 0, равное А0, с помощью ряда Тейлора:

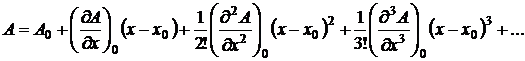(2.1)

Подстановка в это уравнение значений x=x0 + ph и х=х0-h дает значения потенциала соответственно в узлах 1 и 3:

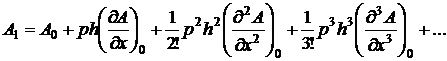(2.2)

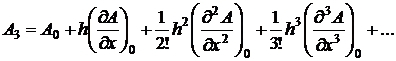(2.3)

Суммировав (2.2) и (2.3) после умножения последнего на р, получим:

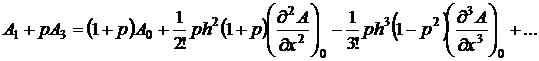(2.4)

и, пренебрегая членами, содержащими А в третьей и более высоких степенях, что допустимо, если h мало, придем к простому выражению для (д2А/дх2)0:

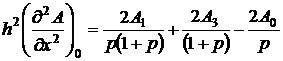(2.5)

Точно таким же способом можно получить выражение для (д2А/ду2)0:

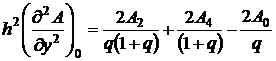(2.6)

Далее, подстановка найденных значений (д2А/дх2)0и (д2А/ду2)0 в уравнение Пуассона, где для более компактной записи член заменен W, дает:

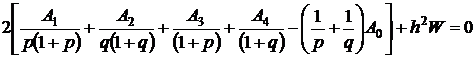(2.7)

Это уравнение (при небольшом значении h) является хорошей аппроксимацией уравнения Пуассона и может его заменить. Однако необходимо подчеркнуть, что в то время как дифференциальное уравнение относится к любой точке поля, каждое уравнение в конечных разностях справедливо только для одной точки (хотя вид уравнений одинаков для всех точек).

Уравнение (2.7) имеет несколько частных модификаций, наиболее важная из которых относится к симметричной звезде (рисунок 2.11б). Уравнение, относящееся к узлу 0 этой звезды, может быть использовано для подавляющего большинства узлов в любой задаче; его нетрудно получить, положив в уравнении (2.7) p = q = 1:

(2.8)

Для узлов, расположенных в областях, где поле описывается уравнением Лапласа, требуемые уравнения для асимметричной и симметричной звезд можно найти соответственно из уравнений (2.7) и (2.8), положив W=0. Кроме того, в случае таких полей эти уравнения могут быть составлены для скалярного потенциала ψ или для функции потока j, поэтому, например, уравнение Лапласа для скалярного потенциала узла, не примыкающего к границе, имеет вид:

(2.9)

Полученные выше уравнения в конечных разностях являются, конечно, только аппроксимациями уравнений поля, поскольку в уравнении (2.4) мы пренебрегли членами высших порядков (соответствующая погрешность называется сеточной). Важно тщательно исследовать эту погрешность, однако на данном этапе достаточно сказать, что практически в любой задаче нетрудно задаться таким значением h, что ошибка будет пренебрежимо малой.

Рассмотрим подход к формулировке задачи по определению поля в виде системы совместных уравнений и для конкретности обратимся к простой типичной области поля, описываемого уравнением Пуассона, внутри квадратной границы, изображенной на рисунке 2.12.

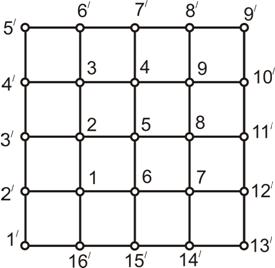
Рисунок 2.12 – Квадратная равномерная сетка

Обозначим узлы на границе номерами со штрихом от 1 до 16 , а внутренние узлы номерами от 1 до 9. Значения W и потенциала на границе заданы, и на первом этапе решения требуется определить значения потенциала 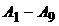для внутренних узлов. Это нетрудно сделать, применив уравнение (2.8) для каждого из внутренних узлов. Для внутреннего узла 1 имеем:

для узла 2

Аналогичные уравнения могут быть составлены и для остальных узлов 3-9. Следовательно, девять значений потенциала связаны между собой и с граничными условиями девятью линейными уравнениями и их можно найти в результате совместного решения этих уравнений.

Точно так же любую задачу по определению поля можно свести к решению системы совместных линейных уравнений в конечных разностях. Для задач с криволинейными границами или с границами, по каким-либо другим причинам не совпадающими с узлами сетки, единственное отличие в формулировке по сравнению с простым случаем, рассмотренным выше, заключается в том, что уравнения для узлов, примыкающих к границе, должны быть выведены из общего уравнения в конечных разностях (2.7) (при W=0 для областей лапласова поля).

Прежде чем приступить к рассмотрению способов решения совместных уравнений, для последующего анализа необходимо представить их в матричном виде. Короче говоря, если [М] – матрица коэффициентов при неизвестных потенциалах Ап, [и] – столбцовая матрица неизвестных потенциалов, а [ν] – столбцовая матрица сумм известных потенциалов А'п и постоянных членов h2W (когда они присутствуют), то указанные уравнения могут быть представлены в виде:

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23