Рисунок 2.18 – Представление решения в МКР (а) и МКЭ (б)
Таким образом, существенным отличием МКЭ от метода конечных разностей (МКР) является то, что в МКЭ решение на каждом элементе получается в виде непрерывных (или гладких) функций, в то время как в МКР – в виде сеточной функции (рисунок 2.18).
2.4 МЕТОД ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
Метод интегральных уравнений дает возможность рассчитать магнитное поле в неоднородной среде (катушка, воздух, сталь, вода и т. д.) свести к расчету в однородной (в вакууме, воздухе). При этом неоднородности необходимо заменить вторичными источниками поля: магнитные заряды, источники с объемной или поверхностной плотностью тока, вихревыми токами.
Выделяются два подхода к расчету метода интегральных уравнений.
1. Используются условия на границах между неоднородными в магнитном отношении областями. Задачу расчета вторичных источников необходимо свести к граничным интегральным уравнениям первого и второго рода, которые в последствии приводятся к уравнениям в конечных суммах для подобластей с постоянными или кусочно-постоянными значениями магнитной проницаемости.
2. Название второго подхода – «метод пространственных интегральных уравнений». Основывается данный подход на общем интегральном выражении магнитной индукции через намагниченность деталей магнитной системы при отсутствии, каких либо дополнительных краевых условий. Расчет осуществляется по итерационной схеме с учетом нелинейных характеристик подобластей, на которые разбита магнитная система [9].
3 РАСЧЕТ МАГНИТНЫХ СИСТЕМ
3.1 ИСПОЛЬЗОВАНИЕ ПРОГРАММНОГО КОМПЛЕКСА ELCUT
ПРИ РАСЧЕТЕ МАГНИТНЫХ СИСТЕМ
3.1.1 Общие сведения
Проектировщик испытывает определенную трудность при расчете традиционными методами электромагнитных аппаратов. Связанно это, прежде всего со сложностью конструкций, а так же приходится рассматривать нелинейную магнитную цепь. В настоящее время все большее применение получают метод конечных разностей. При использовании ЭВМ численные методы получают большие преимущества перед аналитическими благодаря простоте алгоритмов расчета, которые состоят из многократно повторяющихся циклов.
Решения, полученные методом конечных разностей, представляют собой совокупность значений описывающих поле функции в дискретных точках, равномерно распределенных по всей области поля. Эти значения находятся путем замены одного описывающего поле дифференциального уравнения с частными производными системой простых уравнений в конечных разностях, которые имеют вид линейных уравнений, связывающих значение потенциала в каждой точке со значениями потенциала в других точках, окружающих ее.
Таким образом, определение поля сводится к решению системы совместных уравнений [7]. При замене уравнений поля системой уравнений в конечных разностях, связывающих значения потенциала в дискретных точках, можно выбрать произвольное пространственное распределение точек. При выборе полностью равномерного распределения точек для каждой из них справедливо уравнение в конечных разностях одного и того же вида и формулировка задачи значительно упрощается. Требуемое распределение обеспечивается расположение точек в «узлах» любой сетки.
Программа ELCUT является разработкой производственного кооператива «ТОР» (Санкт-Петербург).
ELCUT представляет собой интегрированную диалоговую систему программ позволяющую решать следующие плоские и осесимметричные задачи:
· Линейная и нелинейная магнитостатика.
· Магнитное поле переменных токов (с учетом вихревых токов).
· Электростатика.
· Растекание токов в проводящей среде.
· Линейная и нелинейная, стационарная и нестационарная теплопередача.
· Линейный анализ напряженно-деформированного состояния.
· Связанные (мультидисциплинарные) задачи.
С помощью ELCUT можно описать задачу - ее геометрию, свойства сред, источники поля, граничные и другие условия, решить ее с высокой точностью и проанализировать решение с помощью средств цветной графики. С помощью ELCUT можно решать сложные задачи расчета полей и теории упругости на персональных компьютерах, не прибегая к помощи больших ЭВМ или рабочих станций.
· ELCUT может решать нестационарные тепловые задачи с нелинейной теплоемкостью и изменяющимися временными параметрами.
· ELCUT имеет удобный редактор данных, выполняющий ряд функций:
· Ввод временных параметров задачи.
· Задание нелинейной теплоемкости (схоже с другими редакторами нелинейных свойств).
· Полная совместимость со стационарными задачами: пользователь может конвертировать ранее созданные задачи в нестационарные с минимальными изменениями.
· ELCUT позволяет показывать картины поля для различных моментов времени, представляет временные зависимости как на графике так и в таблице.
Особенности расчетов задач магнитостатики в ELCUT
Расчет магнитного поля применяется при проектировании и исследовании различных устройств, таких как соленоиды, реакторы, электрические машины, трансформаторы, магнитные экраны и т. п. Обычно при расчетах магнитного поля представляют интерес такие величины как магнитная индукция, напряженность магнитного поля, магнитостатические силы и моменты, а также потокосцепления с различными обмотками.
Пакет ELCUT может применяться для решения линейных и нелинейных задач магнитостатики в плоской и осе симметричной постановке. Используется формулировка задачи относительно векторного магнитного потенциала.
Основные показатели магнитостатики используемые
программой ELCUT
Свойства сред: воздух, изотропные и ортотропные материалы с постоянной магнитной проницаемостью, линейные и нелинейные постоянные магниты, изотропные ферромагнетики, проводники с током.
Кривые намагничивания ферромагнитных материалов легко могут быть заданы при помощи окна работы с кривыми.
Источники поля: распределенные и сосредоточенные токи, однородное внешнее поле и постоянные магниты.
Граничные условия: заданное значение потенциала (условие Дирихле), заданные значения касательной составляющей индукции (условие Неймана) и условие постоянства потенциала (нулевого потока) на поверхностях сверхпроводников.
Результаты расчета: магнитный потенциал, магнитная индукция, напряженность магнитного поля, силы, моменты, энергия магнитного поля, потокосцепления, собственные и взаимные индуктивности.
Специальные возможности: Интегральный калькулятор может вычислять различные интегральные значения на определенных пользователем линиях и поверхностях. Магнитные силы могут быть переданы в задачу расчета механических напряжений в элементах конструкции (совмещенная магнито-упругая задача).
Структура базы данных задачи
База данных ELCUT, относящаяся к каждой конкретной задаче состоит из нескольких частей. Центральной частью этой базы данных является описание задачи, которое при записи на диск помещается в файл с расширением. pbm. Описание задачи содержит общую информацию о задаче: характер предметной области, разновидность постановки, класс точности расчета и т. д. Кроме этого, описание задачи содержит ссылки на все остальные файлы, составляющие базу данных задачи. К их числу относятся файл геометрии модели, имеющий стандартное расширение. mod и файлы физических параметров, имеющие одно из расширений. des, .dms, .dcf, .dht или. dsa в зависимости от предметной области задачи.
База данных ELCUT, относящаяся к каждой конкретной задаче состоит из нескольких частей. Центральной частью этой базы данных является описание задачи, которое при записи на диск помещается в файл с расширением. pbm. Описание задачи содержит общую информацию о задаче: характер предметной области, разновидность постановки, класс точности расчета и т. д. Кроме этого, описание задачи содержит ссылки на все остальные файлы, составляющие базу данных задачи. К их числу относятся файл геометрии модели, имеющий стандартное расширение. mod и файлы физических параметров, имеющие одно из расширений. des, .dms, .dcf, .dht или. dsa в зависимости от предметной области задачи.
Описание задачи может ссылаться на один или два файла физических свойств. Оба файла физических свойств имеют одинаковый формат и отличаются только функциональным назначением. Обычно первый из них содержит данные, относящиеся только к данной конкретной задаче, в то время как второй может использоваться в качестве библиотеки свойств материалов и стандартных граничных условий, общих для целого класса задач.
Размещение базы данных задачи в нескольких файлах позволяет использовать общие файлы геометрии модели или общие файлы физических свойств одновременно в нескольких похожих задачах.
В процессе решения задачи ELCUT создает еще один файл - файл результатов. Этот файл всегда имеет расширение. res, имя, совпадающее с именем файла описания задачи, и помещается в ту же папку, в которой находится файл описания задачи.
Чтобы создать новое, пустое описание задачи, выбирается позиция «Создать» из меню «Файл» или нажать Ctrl+N и затем указывается Задача ELCUT в списке предлагаемых типов документов рисунок 3.1. В данном окне можно выбрать создание геометрической модели и свойств для задач.
Рисунок 3.1 – Окно создания нового документа
Затем вводится имя и путь для нового описания задачи, причем можно использовать уже существующую задачу как образец рисунок 3.2.
Далее необходимо выбрать параметры новой задачи: тип анализа, класс симметрии, точность решения, единицы измерения длины и др. Геометрию и свойства задачи можно выбрать из ранее созданных файлов рисунок 3.3.
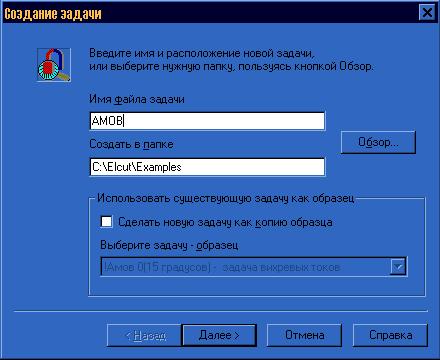
Рисунок 3.2 – Окно создания новой задачи
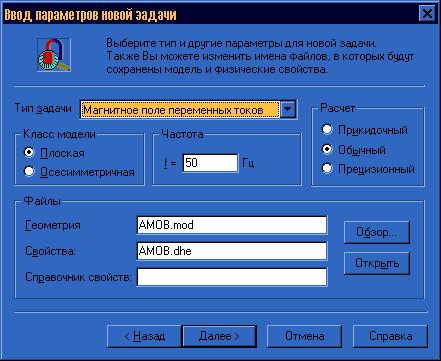
Рисунок 3.3 – Окно ввода параметров новой задачи
Для задачи магнитного поля переменных токов необходимо указать частоту f.
Чтобы открыть существующий документ, необходимо выбрать позицию «Открыть» из меню «Файл» или перетащить файл в окно ELCUT из проводника Windows или нажать Ctrl+O.
Для того чтобы сохранить созданный документ, выбирается позиция «Сохранить» из меню «Файл» или нажимается Ctrl+S. При выборе позиции «Сохранить как …» из меню «Файл» можно сохранить документ, предварительно указав его имя и место расположение рисунок 3.4.
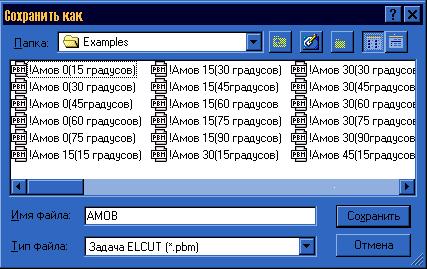
Рисунок 3.4 – Окно сохранение документа
Рабочее окно программы ELCUT состоит из меню, ряда функциональных клавиш, окна структуры и модели задачи рисунок 3.5.
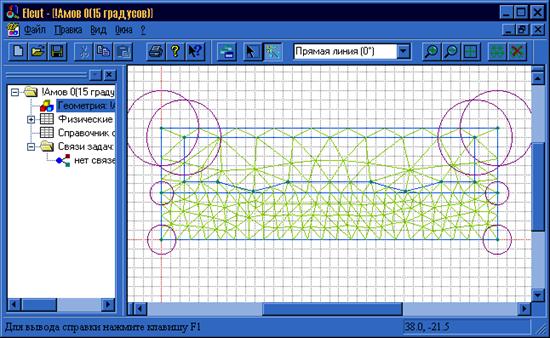
Рисунок 3.5 – Рабочее окно программы ELCUT
3.1.2. Создание геометрического объекта
В программном комплексе ELCUT реализовано создание геометрической модели объекта, для этого используется окно модели.
Геометрическая модель – это один из видов документов ELCUT, который содержит полное описание геометрии задачи. Он содержит различные геометрические объекты и устанавливает связи между ними и свойствами материалов, источниками поля и граничными условиями.
ELCUT предоставляет несколько способов управления изображением модели на экране, которые можно использовать, чтобы изображение было максимально удобным для выполняемой в данный момент работы:
· Масштабирование изображения;
· Видимость деталей модели;
· Сетка привязки.
Можно также открыть несколько окон для одной и той же модели, выбирая в каждом из них разный масштаб и степень детализации изображения. Чтобы сделать это, выбирается команда «Новое окно» в меню «Окна», или воспользуйтесь соответствующей кнопкой на панели инструментов. Для различных манипуляций с окнами можно использовать соответствующие функции в меню «Окна» рисунок 3.6.
Рисунок 3.6 – Меню задания свойств окон
Чтобы сделать изображение более крупным:
1. Нажимается кнопка «Крупнее» на панели инструментов модели.
2. Перемещается мышь с нажатой кнопкой так, чтобы интересующая область, которая затем займет все окно модели, оказалась внутри получившейся рамки.
Чтобы увидеть более обширную часть модели:
· Нажимается кнопка «Мельче» на панели инструментов модели.
· Или, можно нажать кнопку «Показать все» на панели инструментов, чтобы увидеть модель целиком, так крупно, как это возможно.
Вершина, ребро и блок – это три основных типа геометрических объектов, из которых строится модель в системе ELCUT. Рассмотрим более подробно эти понятия.
Вершина – это точка на плоскости, координаты которой введены пользователем или вычислены автоматически как результат пересечения ребер. Для каждой вершины можно задать шаг дискретизации и метку. Величина шага дискретизации задает примерное расстояние между соседними узлами сетки конечных элементов поблизости от данной вершины. Метка используется, на пример, для задания линейного источника поля или нагрузки.
Ребро – отрезок прямой или дуга окружности, соединяющая две вершины, и не пересекающая другие ребра модели. Если новая создаваемая сторона проходит через существующую вершину, то будут созданы два новых ребра, соединенные в данной вершине. Если новое ребро пересекает существующие стороны, то все точки пересечения станут вершинами, а пересекающиеся ребра будут разбиты на части. В качестве первого шага при дискретизации области ребра разбиваются на элементарные отрезки в соответствии с шагами, заданными в вершинах. Ребру может быть присвоена метка, например, для описания краевого условия.
Блок – непрерывная, возможно не односвязная, область, граница которой образована ребрами и, возможно, изолированными вершинами. Блок может содержать отверстия, образованные замкнутыми или разомкнутыми цепочками ребер или изолированными вершинами. Для описания физических свойств среды каждому блоку, входящему в расчетную область, должна быть присвоена метка. Помимо описания свойств среды, метки блоков также используются для задания распределенных источников поля. Сетка конечных элементов создается в каждом блоке автоматически или с учетом шага дискретизации, заданного в отдельных вершинах. В непомеченных блоках расчет поля не производится независимо от того, построена ли в них сетка конечных элементов.
Метка – текстовая строка длиной от 1 до 16 символов, служащая для установления соответствия между геометрическими элементами модели и приписанными им физическими параметрами. Допускаются произвольные печатные символы, включая русские и латинские буквы, цифры, знаки препинания, пробел и другие символы. Не допускаются символы «*» и «?», метка не может начинаться с пробела, а пробелы в конце метки игнорируются. Заглавные и прописные буквы считаются различными.
Шаг дискретизации – имеющая размерность длины величина, сопоставленная вершине модели и задающая густоту сетки в прилегающей области. Задавая шаги дискретизации, можно управлять густотой сетки конечных элементов и, тем самым, точностью решения в тех или иных частях расчетной области.
Обычно, создание модели реализуется в три этапа:
· Ввод геометрических объектов и манипуляция ими;
· Задание свойств, источников поля и граничных условий;
· Построение сетки конечных элементов.
Описывая геометрию модели, задаются вершины и ребра, ограничивающие подобласти (блоки) с различными физическими свойствами. Можно создавать новые вершины и ребра, перемещать, дублировать и удалять любые геометрические объекты. Для выполнения операций над несколькими объектами одновременно, можно использовать механизм выделения.
Чтобы создать новые вершины, необходимо выполнить следующие операции:
1. Выбирается команда Режим вставки в меню Правка или в контекстном меню (правая кнопка мыши), либо можно нажать клавишу INS для перехода в режим вставки рисунок 3.7.
2. Убедится, что текущие параметры сетки привязки подходят для ввода координат узлов, которые будут создаваться.
3. Используя мышь или клавиши ДВИЖЕНИЯ КУРСОРА, помещается курсор в то место, где должна появиться новая вершина, и дважды необходимо щелкнуть левой кнопкой мыши или нажать клавишу ENTER.
4. Необходимо выключить «Режим вставки», когда заканчивается работа по созданию объектов - иначе можно легко создать нежелательные объекты!
Рисунок 3.7 – Окно правки объекта
Для создания линии можно воспользоваться вторым способом:
1. Выбрать пункт «Добавить вершины» в меню «Правка» рисунок 3.8.
2. Ввести координаты новой вершины и нажать кнопку «Добавить». Повторять это необходимое количество раз.
3. Нажать кнопку «Закрыть».
Рисунок 3.8 – Окно добавления вершин
Чтоб создать новые ребра необходимо:
1. Выбрать команду «Режим вставки» в меню «Правка» или в контекстном меню (правая кнопка мыши), либо нажмите клавишу INS для перехода в режим вставки.
2. Используя выпадающий список в панели инструментов модели для выбора типа новых ребер (отрезок или дуга) и угол раствора дуги. Можно использовать имеющиеся в списке величины углов или ввести любое другое значение; нулевой угол обозначает отрезок прямой рисунок 3.9.
3. Необходимо переместить курсор от начальной к конечной точке создаваемого ребра с помощью передвижения мыши, удерживая нажатой ее левую кнопку, либо с помощью клавиш ДВИЖЕНИЯ КУРСОРА при нажатой клавише SHIFT. Можно использовать существующие вершины в качестве концов нового ребра либо создавать новые вершины заодно с созданием ребра. Если включен режим привязки к сетке, новые вершины могут быть созданы только в узлах координатной сетки.
4. Необходимо выключить режим вставки, когда заканчивается работа по созданию объектов - иначе можно легко создать нежелательные объекты!
Рисунок 3.9 – Окно выбора формы ребра
Чтобы выделить геометрические объекты необходимо выполнить следующие пункты:
1. Убедиться, что режим вставки выключен.
2. Щелкнуть мышью объекты, которые необходимо выделить, удерживая при этом нажатой клавишу SHIFT или CTRL, или переместить мышь с нажатой левой кнопкой так, чтобы слитно расположенные объекты оказались внутри получившейся рамки. В последнем случае выделенными окажутся только те объекты, которые целиком умещаются внутри рамки.
Можно также использовать команды «Выделить все» и «Отменить выделение» в меню «Правка» или в контекстном меню. Заметим, что можно одновременно выделить объекты разных типов (блоки, ребра или вершины).
Кроме того, когда выделяется одна из меток в окне описания задачи, все геометрические объекты, имеющие эту метку, становятся выделенными рисунок 3.10.
Рисунок 3.10 – Выделение ребер объединенных в одну группу
Копирование и перемещение геометрических объектов
Повторяющиеся геометрические объекты легко могут быть созданы путем копирования или перемещения любого набора объектов на новом месте. Чтобы сделать копию (продублировать объекты) необходимо:
1. Выделить любое количество объектов (блоков, ребер и вершин), которые необходимо скопировать.
2. Выбрать команду «Дублировать выделенное» в меню «Правка» или контекстном меню. Появится диалог для ввода параметров геометрической трансформации рисунок 3.11.
3. Выбрать метод, ввести его параметры и нажать OK. Создаваемые объекты появятся на экране, и программа спросит подтверждение на их включение в модель. Таким образом, можно убедиться в правильности ввода параметров.
4. Необходимо нажать кнопку «Yes», чтобы подтвердить копирование. Новые объекты будут встроены в модель, и выделенным окажется последняя их копия.
Рисунок 3.11 – Окно перемещение объектов
Операция копирования сохраняет все явно заданные свойства исходных объектов, включая метки и шаги дискретизации. Не копируется только сетка конечных элементов.
Предупреждение. Использовать операцию копирования необходимо с осторожностью, поскольку неверный набор параметров может привести к созданию новых объектов в ненужном месте. Эти ненужные объекты могут накладываться на старые объекты, порождая, тем самым, множество ненужных вершин в местах пересечения ребер. Их последующее удаление может оказаться трудоемким делом.
Можно также переместить выделенные объекты на новое место, соблюдая определенные ограничения: топология области при этом не должна претерпевать изменений и не должно образовываться никаких новых пересечений или соприкосновений. Чтобы переместить выделенные объекты, выберите команду «Переместить выделенное» в меню «Правка» или в контекстном меню. Появится диалог для ввода параметров геометрической трансформации рисунок 3.11.
Чтобы удалить геометрические объекты необходимо:
1. Выделить объекты, которые необходимо удалить.
2. Выбрать команду «Удалить выделенное» в меню «Правка» или в контекстном меню.
Если выделены только вершины и удаляемая вершина является точкой соприкосновения ровно двух сторон, которые могут рассматриваться как одна после удаления этой вершины, стороны соединяются воедино. Иначе программа запрашивает подтверждение на удаление всех сторон, примыкающих к удаляемой вершине.
3.1.3 Задание свойств объекта и решение задачи
Соответствие между геометрическими элементами модели и приписанными им свойствами материалов, граничными условиями и источниками поля устанавливается с помощью меток.
Чтобы присвоить метку объекту необходимо:
1. Выделить объект.
2. Выбрать команду «Свойства» в меню «Правка» или контекстном меню.
3. Введите имя метки и нажмите OK.
Если одновременно выделить объекты разного типа, то можно задать метки для объектов каждого типа (блоки, ребра или вершины) отдельно, пользуясь разными вкладками окна свойств.
Задание свойств для выделенных объектов
Чтобы задать свойства выделенных объектов необходимо:
1. Выделить объект.
2. Выбрать команду «Свойства» в меню «Правка» или контекстном меню рисунок 3.12.
3. Для просмотра свойств можно воспользоваться клавишами ALT+ENTER или двойным щелчкам мыши
Рисунок 3.12 – Окно свойства выделенного объекта
Создание свойств блоков
Для того чтобы создать свойства для нового блока необходимо в окне структуры задачи вызвать контекстное меню при помощи правой клавиши мыши, предварительно поместив курсор на папке «Метки блоков». Затем выбирается пункт «Создать метку» рисунок 3.13.
В свойствах метки блока, задаются ряд компонентов рисунок 3.14:
· Магнитная проницаемость (абсолютная, относительная);
· Полный ток или плотность тока;
· Коэрцитивная сила магнита;
· Выбор координат.
Рисунок 3.13 – Создание новой метки блока
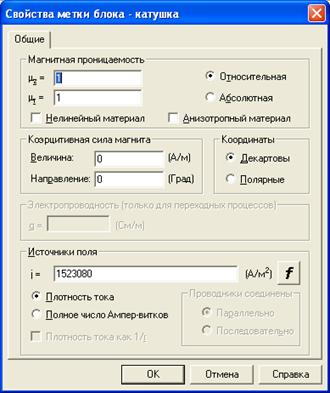
Рисунок 3.14 – Окно свойства метки блока
В ферромагнитных материалах необходимо задать кривую намагничивания вместо магнитной проницаемости рисунок 3.15.
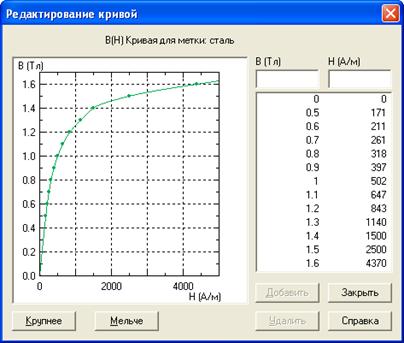
Рисунок 3.15 – Окно редактирования кривой намагничивания
Создание свойств метки ребра
Для того чтобы создать свойства для нового ребра необходимо в окне структуры задачи вызвать контекстное меню при помощи правой клавиши мыши, предварительно поместив курсор на папке «Метки ребер». Затем выбирается пункт «Создать метку».
В свойствах метки ребра, задаются ряд компонентов рисунок 3.16.:
· Магнитный потенциал: А=А0;
· Касательное поле: Ht=s(DHt=s);
· Нулевой нормальный поток: Bn=0.
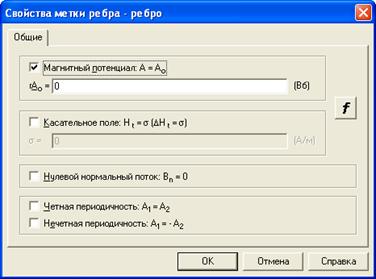
Рисунок 3.16 – Свойства метки ребра
Свойства метки ребра задается для одного из возможных граничных условий. Условие Дирихле, задающее на части границы наперед известный векторный магнитный потенциал А0 в вершине или на ребре модели. Это граничное условие определяет поведение нормальной составляющей индукции на границе. В программе ELСUT условие Дирихле задается как функция координат в виде:
A0 = a + bx + cy – для плоских задач.
rA0 = a + bzr + cr2/2 – для осе симметричных задач.
Константы a,b и с постоянны в пределах стороны, но могут и меняться от одной части границы к другой.
После описания геометрии объекта необходимо построить, конечно-элементную, сетку. Густота сетки непосредственно влияет на точность решения в тех или иных частях расчетной области. Сетка делается особенно густой в местах, где необходимо получить большую точность. Густота сетки управляется заданием шагов дискретизации в вершинах. Шаг дискретизации определяет расстояние между соседними узлами сетки в окрестности, данной вершины рисунок 3.17.
Чтобы построить сетку конечных элементов необходимо:
· Выбрать команду «Построить сетку» в меню «Правка» или в контекстном меню. Затем выберите подходящий вариант в подменю.
· Или, нажать кнопку «Построить сетку» на панели инструментов модели. В этом случае, часть модели, в которой будет построена сетка, выбирается в следующем порядке:
· Выделенные блоки, если они есть;
· Помеченные блоки, если они есть;
· Все блоки модели.
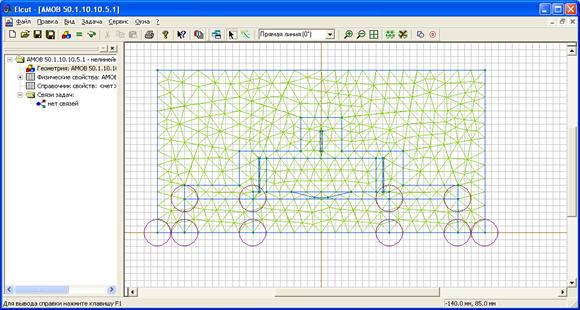
Рисунок 3.17 – Сетка конечных элементов
Управление видимостью дискретизации модели
Рисунок 3.18 – Окно управления дискретизацией
Для управления видимостью дискретизации модели необходимо воспользоваться меню Вид содержащего четыре переключателя рисунок 3.18:
· Сетка конечных элементов;
· Декомпозиция области;
· Дискретизация ребер;
· Шаги дискретизации.
Эти переключатели влияют на степень видимости дискретизации. Если все они выключены, модель изображается без дискретизации. Этот режим удобен при описании модели и расстановке меток.
Если включен один из режимов:
· Шаги дискретизации – все явно заданные величины шагов будут изображаться в виде окружностей соответствующего радиуса.
· Дискретизация ребер – разбиение сторон изображаются штриховыми метками. Сочетание этих двух режимов удобно при расстановке шагов дискретизации.
· Сетка конечных элементов – позволяет видеть сетку треугольников в блоках, где она построена. Этот режим рекомендуется включать при триангуляции блоков.
· Включение режима «Декомпозиция области», при выключенном «Сетка конечных элементов», показывает под блоки, получающиеся в результате процесса геометрической декомпозиции.
Решение задачи
Для решения задачи необходимо выбрать пункт «Решить задачу» в меню вызванным правой клавишей мыши, предварительно поместив курсор в окно описания задачи рисунок 3.19.
Рисунок 3.19 – Окно решения задачи
После решения задачи на экране появляется картина поля рисунок 3.20.
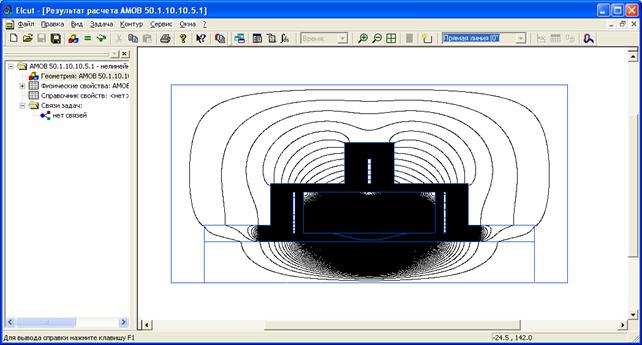
Рисунок 3.20 – Картина поля
3.1.4 Анализ полученных данных
Работа с картиной поля
Когда используется команда анализа решения, ELCUT открывает новое окно, в котором изображается картина вычисленного поля. В этом окне можно:
· При помощи команды «Картина поля» выбрать способы графического представления полевых характеристик, их масштабы и диапазоны;
· Установить масштаб изображения;
· Вывести локальные значения полевых величин в указанных точках;
· Создавать и модифицировать контур;
· Вычислять интегральные характеристики;
· Строить графики;
· Выводить таблицы.
Картина поля может быть скопирована в буфер обмена Windows или сохранена в файле.
Картина поля с цветовой картой оснащается цветовой шкалой.
Можно одновременно работать с несколькими разными картинами поля для одной и той же задачи. Чтобы открыть новое окно, выбирается пункт Новое окно в меню Окна или можно воспользоваться соответствующей кнопкой на панели инструментов.
Чтобы задать условия отображения картины поля необходимо выбрать пункт «Картина поля…» в меню вызванном правой клавишей мыши, предварительно поместив курсор мыши в область картины поля рисунок 3.21.
Рисунок 3.21 – Окно выбора операций
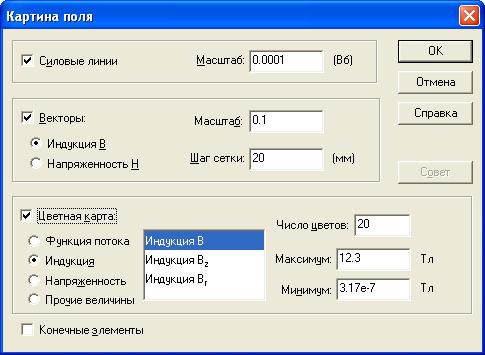
Рисунок 3.22 – Окно параметров картины поля
Картина поля в задачах электростатики может изменять ряд параметров рисунок 3.22:
· Флажок Изолинии потенциала управляет видимостью линий равного потенциала. Необходимо использовать пункт «Масштаб» для изменения густоты линий.
· Векторы показывают величину и направление электрического поля (напряженности или электрического смещения) в виде семейства направленных отрезков.
· Цветная карта изображает пространственное распределение выбранной величины.
· При вводе любого из масштабных параметров можно воспользоваться кнопкой Совет, которая подскажет стандартное значение параметра, вычисленное для наилучшего показа видимой части области.
Изменение масштаба
Чтобы сделать изображение крупнее необходимо:
1. Нажать кнопку «Крупнее» на панели инструментов.
2. Перемещая мышь с нажатой левой кнопкой, выделить прямоугольник, который после отпускания кнопки займет окно целиком.
Чтобы увидеть более обширную часть модели необходимо:
· Нажать кнопку «Мельче» на панели инструментов модели.
· Или, нажать кнопку «Показать все» на панели инструментов, чтобы увидеть модель целиком, так крупно, как это возможно.
Просмотр локальных значений
Чтобы получить значения физических величин, характеризующих поле, в указанных точках, необходимо щелкнуть значок 
на панели инструментов или выбрать команду «Локальные значения» в меню «Вид» или в контекстном меню окна картины поля.
Если панель калькулятора уже открыта, дважды щелкните метку «Локальные значения» в дереве. Появится сообщение, приглашающее пользователя указать мышью точку, в которой необходимо узнать значения поля.
Теперь можно щелчком мыши указывать точки, в которых нужно узнать значения физических величин. Содержимое окна локальных значений обновляется с каждым щелчком. Объемом информации в окне можно управлять двойным щелчком на строки, являющиеся заголовками для других, детализирующих строк рисунок 3.23.
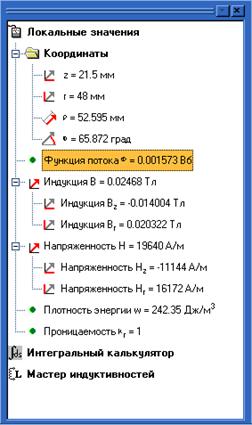
Рисунок 3.23 – Окно локальных значений
Чтобы завершить этот режим, закройте окно локальных значений или выберите команду «Локальные значения» еще раз.
Значения физических величин, показываемые в окне, обеспечивают дополнительные возможности управления:
· Чтобы ввести координаты пробной точки с клавиатуры, выбирается мышью любое из значений координат и затем необходимо щелкнуть по нему мышью еще раз (через некоторый промежуток времени, чтобы не спутать это действие с двойным щелчком мыши). Можно вводить декартовы или полярные координаты.
· Двойной щелчок мышкой над названием физической величины высвечивает цветную карту ее распределения в окне картины поля.
· Можно отметить одну или несколько строк в окне (не обязательно подряд) и экспортировать их в другую программу (например, текстовый процессор или электронную таблицу).
· Содержимое окна локальных значений может быть скопировано в буфер обмена, например, для вывода на печать или для передачи в другую программу, Для этого необходимо воспользоваться командой «Копировать» в буфер в контекстном меню. Чтобы увидеть и скопировать ровно те строки, которые необходимо, пользователь может раскрывать и свертывать отдельные ветви дерева значений.
· Контекстное меню окна значений обеспечивает также быстрый доступ к некоторым органам управления картиной поля, которые обычно используются в диалоге «Картина поля».
Панель калькулятора
Панель калькулятора обычно причалена к левому краю окна картины поля.
Чтобы открыть панель калькулятора, необходимо щелкнуть значок 
на панели инструментов или выбрать команду «Калькулятор» в меню «Вид». Панель калькулятора также откроется при выборе команд «Локальные значения», «Интегральные значения» или «Мастер» в меню «Вид».
Панель калькулятора организована в виде нескольких деревьев, корневые элементы которых соответствуют различным видам числовых данных. Среди них:
– Локальные значения отображают различные полевые характеристики в указанных пользователем точках расчетной области;
– Интегральный калькулятор перечисляет характеристики, которые могут быть вычислены интегрированием по заданной линии, поверхности или объему;
– Мастер индуктивности запускает мастер, который поможет вычислить собственную или взаимную индуктивность катушек или проводников;
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
