4. Определяем по выборке долю продавцов, выработка которых составляет 150 тыс. руб. и более. В соответствии с данными таблицы доля таковых w=0,19+0,08=0,27 (или 27%).
5. Исчисляем среднюю ошибку доли
![]() (или 5,6%)
(или 5,6%)
6. Определяем пределы генеральной доли.
Предельная ошибка доли ![]() при при Рдов = 0,954 (t = 2) составляет 2*0,056=0,112 (или 11,2%).
при при Рдов = 0,954 (t = 2) составляет 2*0,056=0,112 (или 11,2%).
Тогда доверительный интервал для генеральной доли 27 – 11,2 ≤ р ≤ 27 + 11,2,
15,8 ≤ р ≤ 36,2%.
Следовательно, с вероятностью 95,4% доля продавцов, имеющих выработку 150 тыс. руб, и более заключена в интервале от 15,8% до 36,2% и только в 46 случаях из 1000 (1000 – 954) возможна ситуация, когда выборочная доля будет выходить за эти пределы.
Задача 3 (ряды динамики). Используя взаимосвязь показателей динамики, определить уровни ряда динамики и недостающие в таблице цепные показатели динамики по следующим данным о товарообороте специализированного магазина по продаже бытовой техники за 2001-2005гг.(известные данные в таблице выделены жирным шрифтом, рассчитанные - курсивом).
Год | Товарооборот, млн руб. | Цепные показатели динамики | |||
абсолютный прирост, млн руб. | темп роста, % | темп прироста, % | абсолютное значение 1% прироста, млн руб. | ||
2001 | 13,30 | - | - | - | - |
2002 | 14,55 | 1,25 | 109,4 | 9,4 | 0,133 |
2003 | 15,20 | 0,65 | 104,5 | 4,5 | 0,146 |
2004 | 16,50 | 1,30 | 108,6 | 8,6 | 0,152 |
2005 | 17,90 | 1,40 | 108,5 | 8,5 | 0,165 |
Р е ш е н и е:
Решение задачи целесообразно начать с определения отсутствующих в таблице уровней ряда динамики, используя для этого данные об уровне предыдущего года и об одном из известных показателей динамики. Процедура расчета в этом случае выглядит следующим образом:
· уровень 2001г. находим, используя уровень 2002г. и абсолютный прирост в 2002г.:
![]()
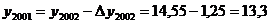 млн руб.;
млн руб.;
· уровень 2003г. определяется так:
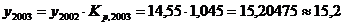 млн руб.
млн руб.
· при определении уровня 2004г. исходим из того, что в 2005г. каждый процент прироста составлял 0,165 млн руб. Следовательно, уровень 2004г., принимаемый за 100%, составил 16,5 млн руб. (т. е. в 100 раз больше абсолютного значения 1% прироста);
· уровень 2005г.:
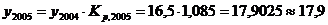 млн руб.,
млн руб.,
где 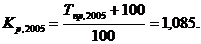
Далее выполняется расчет всех недостающих показателей динамики, которые затем заносятся в таблицу (курсив).
Подход к расчету базисных показателей динамики остается таким же, как и в рассмотренной задаче, только необходимо иметь в виду, что исчислять показатели необходимо по отношению к одному и тому же – базисному – году.
Задача 4 (сводные индексы). Известны следующие данные о реализации продовольственной продукции сельскохозяйственным кооперативом за два периода:
Продовольственная продукция | Реализовано | Цена за единицу, руб. | Расчетные графы (стоимость продукции, тыс. руб.) | ||||
|
|
|
|
|
|
| |
Картофель, кг | 8000 | 9200 | 12 | 14 | 96,0 | 128,8 | 110,4 |
Молоко, л | 16200 | 21800 | 9 | 8 | 145,8 | 174,4 | 196,2 |
Яйцо, шт. | 34250 | 32500 | 2,4 | 2,8 | 82,2 | 91,0 | 78,0 |
Итого | 324,0 | 394,2 | 384,6 |
Определить сводные индексы стоимости продукции, физического объема и цен (по Пааше).
Р е ш е н и е:
1.Определяем сводный индекс стоимости продукции (выручки от продажи):
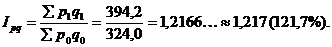
Стоимость продукции (выручка от продажи) в отчетном периоде увеличилась на 21,7% (121,7-100), что в абсолютном (денежном) выражении составило:
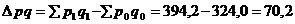 тыс. руб.
тыс. руб.
2. Определяем сводный индекс физического объема продукции:
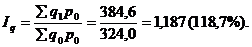
В целом по кооперативу объем реализации продукции увеличился на 18,7% (118,7 – 100).
В абсолютном выражении увеличение стоимости за счет изменения объема реализации составило:
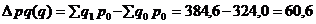 тыс. руб.
тыс. руб.
3. Определяем сводный индекс цен (по Пааше):
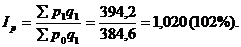
Полученный результат означает, что цены на продукцию кооператива в среднем повысились на 2% (102 – 100).
Остановимся несколько более подробнее на экономической сущности индекса цен. В этом индексе числитель ![]() - реальная величина, фактическая выручка, полученная от реализации продукции в отчетном периоде, а знаменатель
- реальная величина, фактическая выручка, полученная от реализации продукции в отчетном периоде, а знаменатель ![]() - условная величина, показывающая, какой была бы выручка, при условии, что продукция в отчетном периоде продавалась бы по ценам базисного периода. Разность между ними
- условная величина, показывающая, какой была бы выручка, при условии, что продукция в отчетном периоде продавалась бы по ценам базисного периода. Разность между ними ![]() тыс. руб. показывает, какую реально прибыль получил кооператив в отчетном периоде за счет изменения цен.
тыс. руб. показывает, какую реально прибыль получил кооператив в отчетном периоде за счет изменения цен.
4. Проверяем увязку индексов и абсолютных изменений:

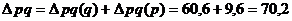 тыс. руб.,
тыс. руб.,
что соответствует ранее полученным цифрам.
5. Определяем долю каждого фактора в общем абсолютном размере изменения результативного показателя:
· физического объема продукции
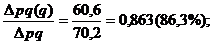
· изменения цен
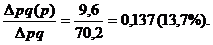
Рассмотренный пример показывает, что для исчисления сводных индексов в агрегатной форме требуется следующая система данных ![]() или
или ![]() по всей исследуемой совокупности товаров (продукции), или данные в другой форме, позволяющие найти
по всей исследуемой совокупности товаров (продукции), или данные в другой форме, позволяющие найти ![]() по каждой разновидности товаров (продукции).
по каждой разновидности товаров (продукции).
Задача 5 (индексы сводных величин). По акционерному обществу, состоящему из трех предприятий, известны данные о выпуске и себестоимости одноименной продукции в базисном и отчетном периодах (табл. 1).
Таблица 1
Номер предприятия | Базисный период | Отчетный период | Расчетные графы | ||||||
Выпуск продукции | Себестоимость единицы продукции, руб. | Выпуск продукции | Себестоимость единицы продукции, руб.
|
тыс. руб. |
тыс. руб |
тыс. руб | |||
тыс. единиц
| в долях к итогу
| тыс. единиц
| в долях к итогу
| ||||||
1 | 10 | 0,50 | 15 | 10 | 0,40 | 14,2 | 150 | 142,0 | 150 |
2 | 6 | 0,30 | 13 | 7 | 0,28 | 12,5 | 78 | 87,5 | 91 |
3 | 4 | 0,20 | 10 | 8 | 0,32 | 9,5 | 40 | 76,0 | 80 |
| 20 | 1,00 |
| 25 | 1,00 |
| 268 | 305,5 | 321 |
Определить изменение средней себестоимости единицы продукции в целом по акционерному обществу (по совокупности трех предприятий) в отчетном периоде по сравнению с базисным в относительных величинах и в абсолютном (денежном) выражении.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |




