- индекс цен (по Ласпейресу);

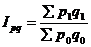- индекс товарооборота.

Увязка индексов в систему .

Разность между числителем и знаменателем каждого из индексов позволяет определить изменение товарооборота в абсолютном выражении в целом и по факторам – за счет изменения цен 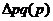и физического объема реализации : , где ; ;

.

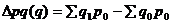Аналогичной системой индексов можно охарактеризовать и процессы, относящиеся к производству продукции в части себестоимости:

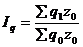- индекс физического объема произведенной продукции;

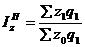- индекс себестоимости (по Пааше);

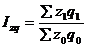- индекс затрат на производство продукции.

Изменение затрат на производство продукции в абсолютном выражении:

в целом 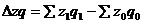; за счет изменения себестоимости единицы продукции каждого вида 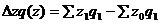; за счет изменения объема производства ; .

Формулы средних индексов из индивидуальных:

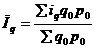- общий индекс физического объема в средней арифметической форме;

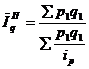- общий индекс цен (по Пааше) в средней гармонической форме.

Разность между числителем и знаменателем этих индексов также дает изменение товарооборота по факторам (за счет изменения физического объема реализации и за счет изменения цен).

Все рассмотренные выше индексы рассчитывались по нескольким товарам, реализуемым в одном месте, или видам продукции, производимым на одном предприятии. Если один и тот же товар реализуется в разных местах или вид продукции производится на ряде предприятий, то динамику таких процессов характеризуют с помощью индексов средних величин, которые представляют собой систему взаимосвязанных индексов переменного состава, постоянного состава и структурных сдвигов.

Средняя цена и средняя себестоимость определяются формулами:

; .

Динамику средних цен характеризуют следующие индексы:

- индекс переменного состава, показывающий, как изменилась средняя цена определенного вида товара, реализованного на разных рынках, за счет двух факторов: р – изменения цен на отдельных рынках и q – изменения количества (доли) товаров, реализованных на разных рынках, т. е. структуры продаж;

- индекс постоянного состава, характеризующий изменение средней цены за счет изменения цен на отдельных рынках;

- индекс структурных сдвигов, характеризующий изменение средней цены за счет структурного фактора, т. е. изменения долей продукции, реализованной на разных рынках (по разным ценам).

Все три индекса увязываются в систему:

.

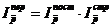Разность между числителем и знаменателем каждой из формул определяет абсолютное изменение средней цены в целом и по указанным факторам .

Изменение товарооборота в абсолютном выражении по совокупности всех рынков определяется по следующим формулам:

·  в целом ;

·  за счет изменения средней цены ;

·  за счет изменения цен на отдельных рынках ;

·  за счет изменения объема продаж ;

·  за счет изменения структуры продаж .

Все рассмотренные изменения товарооборота увязываются в следующие системы:

.

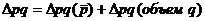
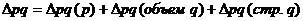Аналогичные формулы можно записать применительно и к себестоимости (заменив соответственно p на z).

5. Примеры решения и оформления задач

Задача 1 (аналитическая группировка). По ряду предприятий отрасли известны данные о средней годовой стоимости основных производственных фондов и фондоотдаче (стоимости продукции в рублях, приходящейся на один рубль основных фондов):

№

пред-

прия-

тия

Стоимость основных производственных фондов, млн руб.

Фондоотдача,

рублей/ рубль

№

пред-

прия-

тия

Стоимость основных производственных фондов, млн руб.

Фондоотдача,

рублей/ рубль

1

26,2

2,75

16

26,5

4,08

2

32,0

3,44

17

29,2

3,30

3

28,2

4,95

18

22,0

3,10

4

24,0

3,45

19

30,4

3,60

5

34,0

3,82

20

26,4

3,95

6

27,0

3,26

21

34,8

4,25

7

21,2

3,05

22

30,0

4,37

8

28,0

3,27

23

21,5

3,60

9

20,5

2,80

24

34,6

4,20

10

27,5

3,48

25

27,2

4,10

11

24,5

2,74

26

23,1

3,10

12

33,0

4,10

27

29,4

3,00

13

27,0

3,76

28

31,2

3,65

14

25,8

3,65

29

29,4

3,25

15

19,0

3,15

30

30,4

3,45

Применяя к исходным данным метод аналитической группировки, выявить характер связи между стоимостью основных фондов, объемом выпуска продукции и средней фондоотдачей (стоимостью продукции в рублях, приходящейся на 1 рубль основных фондов).

При группировке по факторному признаку (стоимости основных фондов) выделить четыре группы предприятий с равными закрытыми интервалами. Величину интервала округлять в верхнюю сторону до ближайшего целого числа. Результаты группировки отразить в итоговой статистической таблице.

В заключение сделать обоснованные выводы:

· о структуре рассмотренной совокупности предприятий по стоимости основных фондов;

· о наличии и характере связи между стоимостью основных фондов, объемом выпускаемой продукции и фондоотдачей.

Р е ш е н и е:

1. В соответствии с условиями задачи в качестве группировочного признака берем стоимость основных производственных фондов и образуем четыре группы предприятий с равными интервалами. Величину интервала определяем по формуле

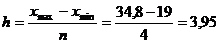млн руб.

Полученное значение округляем в верхнюю сторону до ближайшего целого числа и принимаем величину интервала 4 млн руб.

Обозначаем границы групп (млн руб.):

1-я группа

2-я группа

3-я группа

4-я группа

19-23

23-27

27-31

31-35

2. Строим рабочую таблицу. В таблице выделяем соответствующие группы предприятий, указываем для каждого предприятии стоимость основных производственных фондов, фондоотдачу, рассчитанные объемы продукции (произведение фондоотдачи и стоимости основных фондов), а также приводим исчисленные по каждой группе итоговые результаты.

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15