Методические рекомендации по написанию контрольной работы по дисциплине «Статистика» (стр. 2 )

Предметом статистики являются совокупности тех или иных явлений и процессов, исследование которых связано с количественной характеристикой и выявлением присущих им закономерностей.

Основные категории статистики: статистическая совокупность, единица статистической совокупности, признак, вариация, статистический показатель, система статистических показателей, статистическая закономерность.

Массовое наблюдение, группировка и сводка его результатов, исчисление и анализ обобщающих показателей – все это вместе составляет специфический метод статистики.

Тема 1. Статистическое наблюдение

Статистическое наблюдение представляет собой научно организованный сбор данных об изучаемых массовых явлениях и процессах общественной жизни.

Формы статистического наблюдения: отчетность, специальное статистическое наблюдение.

Способы: непосредственное наблюдение, документальное наблюдение, опрос.

Виды: по времени регистрации (текущее, периодическое, единовременное), по характеру охвата единиц совокупности (сплошное, несплошное).

Тема 2. Сводка и группировка статистических данных

Сводка – это комплекс последовательных операций по обобщению конкретных единичных фактов, образующих совокупность, для выявления типичных черт и закономерностей, присущих изучаемому явлению в целом. Она выполняется с целью привидения результатов в форму, удобную для последующего анализа и осуществляется при помощи метода группировок.

Статистическая группировка – это процесс образования однородных групп на основе расчленения статистической совокупности на группы по какому-либо одному или нескольким определенным, существенным для них признакам, носящим название группировочных признаков.

Различают следующие виды группировок: типологическая (расчленение разнородной совокупности на отдельные качественно однородные группы), структурная (разделение однородной совокупности на группы, характеризующие ее структуру по определенному варьирующему признаку), аналитическая (предназначена для установления тесноты связи между взаимодействующими признаками – факторным и результативным).

Простейшей группировкой является ряд распределения, представляющий собой упорядоченное расположение единиц статистической совокупности по значению какого-либо признака. Ряды распределения подразделяются на атрибутивные (по качественному признаку) и вариационные (по количественному признаку). Различают дискретные и интервальные вариационные ряды. Интервальные вариационные ряды бывают с равными, неравными, закрытыми и открытыми интервалами. При построении вариационного ряда с равными интервалами определяют число групп и величину интервала. Число групп может быть задано или определено по формуле Стерджесса 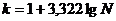, где N – число единиц совокупности. Величина равного интервала рассчитывается по формуле , где хmax и хmin – максимальное и минимальное значение признака.

Для графического отображения вариационных рядов строят гистограмму, полигон и кумуляту распределения.

Тема 3. Обобщающие статистические показатели

Различают три вида обобщающих показателей: абсолютные, относительные и средние.

Абсолютные величины – именованные числа, имеющие определенную размерность и единицы измерения. Они характеризуют показатели на момент времени или за период. Применяются натуральные, условно-натуральные, стоимостные и трудовые единицы измерения.

Относительные величины характеризуют количественные соотношения сравниваемых абсолютных величин. Числитель – сравнимаемая величина, знаменатель – основание или база сравнения. Различают следующие виды относительных показателей: динамики, планового задания и выполнения плана, структуры и координации, сравнения, интенсивности.

Средние величины – одна из наиболее распространенных форм статистических показателей. Используются различные степенные средние: арифметическая, гармоническая, квадратическая, геометрическая и структурные средние: мода и медиана. Наиболее распространенной является средняя арифметическая, которая исчисляется в двух формах: простой 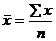и взвешенной , где х – значение признака, n – число единиц признака, f – частота (вес) группы. Также довольно часто используется средняя гармоническая простая 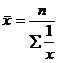и взвешенная 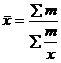, где m = xf - веса для обратных значений x.

Выбор вида средней арифметической или гармонической обусловлен характером исходных данных. Прежде чем приступить к непосредственному расчету, необходимо четко уяснить, соотношением каких показателей является средняя в данном конкретном случае.

Мода – это значение признака, наиболее часто встречающееся в изучаемой совокупности. Медиана – это значение признака, которое расположено в середине ранжированного ряда. В интервальных рядах при определении моды и медианы сначала находят модальный и медианный интервалы, а затем по интерполяционным формулам исчисляют и сами показатели. Моду и медиану можно также определить на основе графического изображения ряда. Мода определяется по гистограмме распределения, а медиана – по кумуляте.

Тема 4. Показатели вариации

Показатели вариации используются для измерения степени колеблемости отдельных значений признака от средней. Основные обобщающие показатели вариации: дисперсия, среднее квадратическое отклонение, коэффициент вариации.

Дисперсия признака представляет собой средний квадрат отклонений вариантов от их средней величины. В зависимости от исходных данных она вычисляется:

для несгруппированных данных по формуле ,

для сгруппированных данных по формуле .

Расчеты дисперсии можно упростить, если использовать формулу , где - средний квадрат значений признака в совокупности: 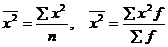, а - квадрат среднего значения признака в совокупности.

Среднее квадратическое отклонение измеряется в тех же единицах, что и варьирующий признак, показывает, на сколько в среднем отклоняются конкретные варианты признака от его среднего значения и исчисляется путем извлечения корня квадратного из дисперсии .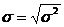

Коэффициент вариации определяется по формуле

.

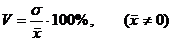Чем больше величина коэффициента вариации, тем больше разброс значений признака вокруг средней, тем менее однородна совокупность по составу. Если коэффициент вариации не превышает 30%, то совокупность считается однородной.

Тема 5. Выборочное наблюдение

Целью выборочного наблюдения является определение параметров генеральной совокупности (генеральной средней и генеральной доли ) на основе параметров выборочной совокупности (выборочной средней и выборочной доли w). Разница между генеральными и выборочными параметрами называется ошибкой выборки. Её значение при собственно случайном и механическом отборе рассчитывается по формулам:

Предельная ошибка выборки определяет собой - кратную среднюю ошибку , где - коэффициент доверия, определяемый по таблице значений интегральной функции Лапласа при заданной доверительной вероятности:

Необходимая численность выборки, обеспечивающая требуемую точность расчета оценок генеральных параметров при собственно случайном и механическом отборе, определяется формулами:

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15