Задание. Необходимо рассчитать годовое количество каждого изделия в производственной программе для двух однокритериальных задач. В первой задаче целевая функция – прибыль предприятия, во второй задаче – трудоемкость производственной программы. Написать программу (использовать метод ветвей и границ) либо использовать встроенные функции Mathcad.

Варианты заданий.

С помощью нормального датчика случайных чисел сгенерировать граничные значения показателей , приведенных в таблице 3, при этом значения, приведенные в табл.3 рассматривать как средние значения. Новое значение показателя рассчитывается по формуле

, ,

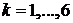где – нормальная случайная величина .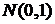

3.4 Лабораторная работа №4. Многокритериальная задача. ОПТИМИЗАЦИЯ ГОДОВОЙ ПРОИЗВОДСТВЕННОЙ ПРОГРАММЫ ПРЕДПРИЯТИЯ МЕТОДОМ СПРАВЕДЛИВОГО КОМПРОМИССА

Работа выполняется на основе результатов лабораторной работы №3.

Метод справедливого компромисса

Для формализации понятия справедливого компромисса нам понадобится ввести отношение превосходства ► на множестве Парето (как уже указывалось, множество Парето можно определить как множество, в котором значение любого из частных критериев оптимальности можно улучшить только за счет ухудшения других частных критериев – любое из решений, принадлежащее множеству Парето, не может быть улучшено одновременно по всем частным критериям) [1]. Множество Парето называют также эффективным множеством.

Пусть во множестве Парето задачи (1) даны две точки , и значения всех частных критериев оптимальности в них . Введем меру относительного изменения (снижения – знак "минус" или повышения – знак "плюс") качества решения по каждому из этих критериев [1]

(1)

критериев оптимальности при переходе от решения к решению . Вычислим максимальное снижение качества решения при переходе от решения к где - абсолютные изменения значений частных решению

. (2)

Аналогично вычислим максимальное повышение качества решения при переходе решения к решению

. (3)

Будем говорить, что решение превосходит решение , и писать ► , если

. (4)

С другой стороны, будем говорить, что решение превосходит решение , если

. (5)

Выбор решений будем производить с помощью полного перебора узлов сетки, покрывающей эффективное множество задачи (1). Поскольку метод справедливого компромисса использует относительные изменения частных критериев оптимальности, этот метод инвариантен к масштабу измерения частных критериев, т. е. не требуется их нормализация.

Для получения оптимальной годовой производственной программы необходимо решить следующую оптимизационную двухкритериальную задачу

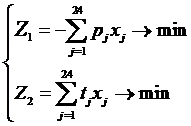(6)

при ограничениях

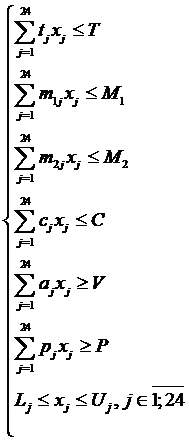(7)

Полученные оптимальные решения двух однокритериальных задач в работе №4 нужно свести в результирующую таблицу. Затем необходимо отметить в строке «Задача 2» «жирным» компоненты решения, которые отличаются от компонент решения «Задачи 1». Этот факт позволит сократить объем вычислений при решении двухкритериальной задачи (1), (2).

Для решения задачи (6) при ограничениях (7) реализуем метод справедливого компромисса (1) – (5). Поскольку решение многокритериальной задачи требует сонаправленности функций цели (все критерии на минимум, либо все критерии на максимум), а в нашем случае один критерий – максимизация прибыли, а другой – минимизация трудоемкости, то необходимо один их них принять со знаком «минус» (см. (6)):

Для решения задачи (6), (7) необходимо искать решение путем полного перебора узлов сетки, покрывающей эффективное множество задачи. С учетом результатов, приведенных в результирующей таблице, перебор узлов сетки производится только по тем номерам переменным, которые выделены «жирным». Значения остальных переменных не изменяются. Диапазоны изменения переменных, отмеченных «жирным», также определяются из результирующей таблицы.

Задание. С помощью пакета MathCad рассчитать оптимальную производственную программу предприятия.

3.5 Лабораторная работа №5. Транспортная задача

Транспортная задача относится к задачам линейного программирования. Ее суть заключается в составлении плана перевозок, при котором весь продукт вывозится от поставщиков к потребителям в соответствие с потребностью и общая величина транспортных издержек будет минимальной. Если суммарный объем производства равен суммарному спросу, то такая модель называется сбалансированной транспортной моделью. В противном случае, модель называется несбалансированной (для ее приведения к сбалансированной вводится фиктивный пункт).

Задание

Заводы производственной фирмы (производство офисных кресел) расположены в городах Омск, Новосибирск, Томск. Центры распределения расположены в городах Нижний Новгород, Пермь, Краснодар. Объемы производства и величина спроса в пунктах представлены в таблице 1. Одно изделие имеет вес 3 кг. и объем 0,8 м3. Стоимость перевозки рассчитайте с помощью онлайн-калькулятора http://www. jde. ru/calc.

Составьте экономико-математическую модель задачи. С помощью пакета MathCAD найдите оптимальное распределение поставок и минимальные затраты на перевозку.

Вариант 1

Таблица 1

Объем производства в пункте	Величина спроса в пункте
Омск	Новосибирск	Томск	Нижний Новгород	Пермь	Краснодар
1000	2000	1200	2000	1100	1100

Вариант 2

Таблица 1

Объем производства в пункте	Величина спроса в пункте
Омск	Новосибирск	Томск	Нижний Новгород	Пермь	Краснодар
1500	1000	800	2000	900	400

Вариант 3

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14