1. Инвесторы производят оценку инвестиционных портфелей, основываясь на ожидаемых доходностях и их стандартных отклонениях за период владения.
2. При выборе между двумя портфелями инвесторы предпочтут тот, который при прочих равных условиях даёт наибольшую ожидаемую доходность.
3. При выборе между двумя портфелями инвестор предпочтет тот, который при прочих равных условиях имеет наименьшее стандартное отклонение.
4. Частные активы бесконечно делимы. Это значит, что инвестор при желании может купить часть акции.
5. Налоги и операционные издержки несущественны.
При этих предположениях можно сформулировать следующую оптимизационную задачу: определить доли вложений 
(
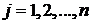) минимизирующие вариацию (риск) портфеля
,
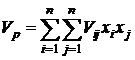при условии, что обеспечивается заданное значение 
ожидаемой эффективности портфеля
.
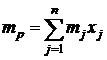Кроме того, должны быть выполнены дополнительные ограничения вида
, 
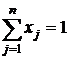при всех .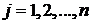
Данная задача с учетом последнего ограничения называется задачей квадратичного программирования.
Задание
Выберите 5 акций различных компаний. Найдите в интернете котировки этих акций на 20хх г. (текущий год) (котировки можно найти на сайте www. finam. ru в разделе «Экспорт»). Сформируйте оптимальный портфель, считая, что продажа будет выполнена в следующем месяце, используя средние значения котировок за каждый месяц (дивиденды не выплачиваются, и поэтому их величина не учитывается).Рекомендации: Найдите в Интернете ежемесячную цену 
продажи акции за последние 24 месяца для каждого вида акций. Рассмотрите процедуру проведения онлайн-торгов и типы регистрируемых цен (last bit, low, high), обоснуйте выбор той или иной цены в качестве величины . После этого рассчитайте доходность 
за каждый месяц для каждого вида акции, а затем – среднее значение доходности для каждого вида акций 
, дисперсию 
и матрицу ковариации 
. Теперь может быть построена модель для нахождения оптимального портфеля.
3.9 Лабораторная работа №9. Динамическое программирование
В задачах динамического программирования процесс принятия решения разбит на шаги, на каждом из которых принимается оптимальное решение, приводящее в максимум значение целевой функции.
Задание (для вариантов 1-8)
Общая сумма в 4 млн. руб. распределяются между тремя предприятиями в количествах, кратных 1 млн. руб. В результате выделения средств 
- му предприятию в размере 
оно дает доход 
, 
, величина которого может быть найдена из таблицы 1.
Используя метод динамического программирования, определить такой план распределения средств между предприятиями, при котором суммарный доход максимален.
1) Решить задачу «вручную». Описать действия, производимые на каждом этапе. Промежуточные результаты свести в общую таблицу.
2) В среде MathCAD напишите программу расчета средств, которые необходимо выделить каждому предприятию. Исходные данные для программы: число предприятий 
, количество вариантов вложений в проект, матрица полученного дохода при заданном вложении.
Вариант 1
Таблица 1.
| 0 | 1 | 2 | 3 | 4 |
| 0 | 5 | 9 | 11 | 12 |
| 0 | 4 | 8 | 12 | 14 |
| 0 | 7 | 9 | 10 | 11 |
Пусть общая сумма увеличилась на 1 млн. руб. Добавьте еще один вариант вложения (Таблица 2).
Таблица 2
| 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 5 | 9 | 11 | 12 | 14 |
| 0 | 4 | 8 | 12 | 14 | 15 |
| 0 | 7 | 9 | 10 | 11 | 12 |
Вариант 2
Таблица 1.
| 0 | 1 | 2 | 3 | 4 |
| 0 | 6 | 10 | 12 | 13 |
| 0 | 4 | 9 | 11 | 14 |
| 0 | 7 | 10 | 11 | 12 |
Пусть общая сумма увеличилась на 1 млн. руб. Добавьте еще один вариант вложения (Таблица 2).
Таблица 2
| 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 6 | 10 | 12 | 13 | 15 |
| 0 | 4 | 9 | 11 | 14 | 16 |
| 0 | 7 | 10 | 11 | 12 | 13 |
Вариант 3
Таблица 1.
| 0 | 1 | 2 | 3 | 4 |
| 0 | 7 | 9 | 11 | 12 |
| 0 | 5 | 8 | 14 | 16 |
| 0 | 8 | 9 | 10 | 11 |
Пусть общая сумма увеличилась на 1 млн. руб. Добавьте еще один вариант вложения (Таблица 2).
Таблица 2
| 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 7 | 9 | 11 | 12 | 14 |
| 0 | 5 | 8 | 14 | 16 | 17 |
| 0 | 8 | 9 | 10 | 11 | 12 |
Вариант 4
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
