3.1. Лабораторная работа № 1
Матричные вычисления с помощью пакета Mathcad
Для выполнения этой работы необходимо написать программы решения СЛАУ, вычисления обратной матрицы и определителя матрицы на основе метода Гаусса. Для проверки работы программы использовать встроенные функции.
Варианты заданий
Вариант №1
Вычислить матрицу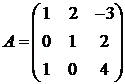
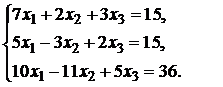
, где 
.
Решить систему уравнений 
Решение получить тремя способами: 1) 
, где 
– матрица системы, 
– правая часть; 2) с помощью функции 
; 3) с помощью функции 
.
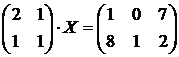
Вид сырья | Нормы расхода сырья на одну пару, усл. ед. | Расход сырья на один день, усл. ед. | ||
Сапоги | Кроссовки | Ботинки | ||
S1 | 5 | 3 | 4 | 2700 |
S2 | 2 | 1 | 1 | 1000 |
S3 | 3 | 2 | 2 | 1600 |
Найти ежедневный объем выпуска каждого вида обуви
Вариант №2
Вычислить матрицу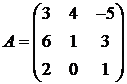
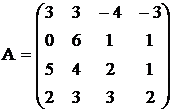
, где 
Решение получить тремя способами: 1) , где – матрица системы, – правая часть; 2) с помощью функции ; 3) с помощью функции .
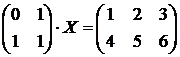Задача. В торговом зале необходимо выставить для продажи товары Т1 и Т2. Рабочее время продавцов составляет 360 ч, а площадь торгового зала, которую можно занять, равна 120 м2. Каждая реализованная единица товара приносит прибыль соответственно 50 и 80 ден. ед. Норма затрат ресурсов на единицу проданного товара приведена в таблице. Ресурсы | Товары | |
Т1 | Т2 | |
Рабочее время, ч. | 0,4 | 0,6 |
Площадь, м2 | 0,2 | 0,1 |
Найти структуру товарооборота и прибыль, соответствующую этой структуре.
Вариант №3
1. Вычислить матрицу 
, где 
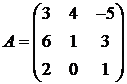
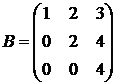
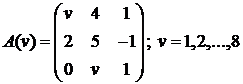Решить систему уравнений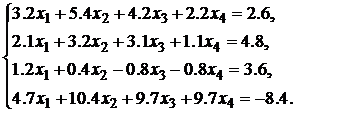 
Решение получить тремя способами: 1) , где – матрица системы, – правая часть; 2) с помощью функции ; 3) с помощью функции .
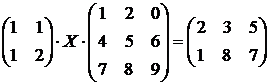Задача. Предприятие производит продукцию трех видов и использует сырье двух типов. Норма затрат сырья на единицу продукции каждого вида 
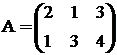
Стоимость единицы сырья каждого типа задана вектором
В = (10, 15).
Каковы общие затраты предприятия на производство 100 единиц продукции первого вида, 200 единиц продукции второго вида и 150 единиц продукции третьего вида?
Вариант №4
Вычислить матрицу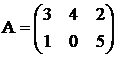
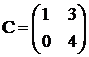
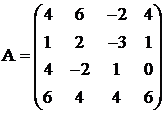, где 
; 
; 
Решить систему уравнений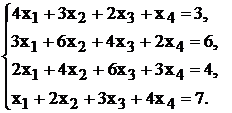 
Решение получить тремя способами: 1) , где – матрица системы, – правая часть; 2) с помощью функции ; 3) с помощью функции .
, если 
; 
; 
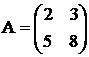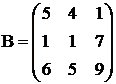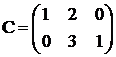
5. Задача. С двух заводов поставляются автомобили для двух автохозяйств. Первый завод выпустил 350 машин, а второй - 150 машин. Затраты 1 автохозяйства на перевозку автомобилей составили 1900 у. д.е., затраты 2 автохозяйства составили 7500 у. д.е Известны затраты на перевозку одного автомобиля с завода в каждое автохозяйство (см. таблицу).
Завод | Затраты на перевозку в автохозяйство, ден. ед. | |
1 | 2 | |
1 | 15 | 20 |
2 | 8 | 25 |
Найти план перевозок машин и общую стоимость перевозок.
Вариант №5
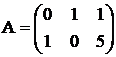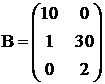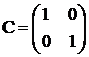
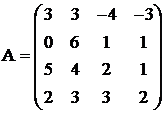Вычислить матрицу, где 
; 
; 
Решить систему уравнений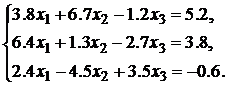 
Решение получить тремя способами: 1) , где – матрица системы, – правая часть; 2) с помощью функции ; 3) с помощью функции .
, если 
; 
;
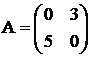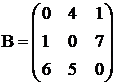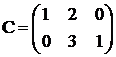
5. Задача. Имеются три банка, каждый из которых начисляет вкладчику определенный годовой процент (свой для каждого банка). Имеется три вкладчика, у каждого из которых в начале года была сумма 6000руб. В начале года вкладчики разместили свои деьги в трех банках. Первый вкладчик 1/3 вклада вложил в банк №1, 1/2 вклада - в банк №2 и оставшуюся часть - в банк №3; к концу года сумма этих вкладов возросла до 7600 руб. Второй вкладчик 1/6 вклада положил в банк №1, 2/3 - в банк №2 и 1/6 - в банк №3; к концу года сумма вклада составила 7400 руб. Третий вкладчик 1/2 вклада положил в банк №1, 1/6 - в банк №2 и 1/3 вклада в банк №3; сумма вкладов в конце года составила 7800 руб. Какой процент выплачивает каждый банк?
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
