Для однозначности будем считать, что сверху обозначены те объекты, на которые воздействуют, справа – те, которые воздействуют (с точки зрения передачи воздействия от давления на педали, тормоза и руль). Воздействие обозначено 1.

Таблица 3. Классификация систем по степени сложности и обусловленности действия.

Таблица 4. Классификация систем по происхождению и характеру поведения (для динамических систем)

Таблица 5. Классификация систем по типу и форме.

Тема 11. Постановка экстремальной задачи на примере задач линейного программирования (4 час.)

Модели, приводящие к постановке задачи линейного программирования. Примеры для самостоятельной работы.

В общем виде, ЗЛП состоит в определении минимального или максимального значения целевой функции; целевая функция и ограничения и представляют собой линейные неравенства.

F(х) = ® Max

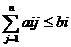
i = 1….k

xj ³ 0,

aij, bi, ci - заданные постоянные величины

Чтобы решить эту задачу, нужно найти такой вектор Х = (x1, x2,… xк)

(набор переменных величин xj), чтобы он доставлял максимальное значение целевой функции F (х)

Пример постановки ЗЛП.

На предприятии изготавливается два вида изделий из трёх видов материалов

aij – расход материала вида i на одно изделие j.

bi - запас материала вида i

ci - прибыль от одного изделия вида i.

Сформулировать ЗЛП, чтобы определить, сколько изделий каждого вида следует производить, чтобы максимизировать прибыль. Расход материалов представлен в Таблице.

Таблица

Расход материала вида i на одно изделие j

Решение

В соответствии с вопросом, сформулированным в задаче, в качестве переменной величины выступит объём производства изделий каждого вида. Тогда:

Х1 - объём производства изделий 1-го вида

Х2 - объём производства изделий 2-го вида

Постановка задачи ЛП:

22Х1 + 14Х2 ® мах (максимизировать совокупную прибыль от

производства изделий обоих видов)

5 Х1 + 7 Х2 £ 456 – ограничение на потребление материалов 1-го вида

2 Х1 + 8 Х2 £ 594 ограничение на потребление материалов 2-го вида

6 Х1 + 4 Х2 £ 872 ограничение на потребление материалов 3-го вида

Х1, Х2 ³ 0 - изделия должны производиться

Тема 12. Обзор задач математического программирования. Построение математической модели по дереву целей

Транспортная задача, задача о назначениях, задачи на графах, квадратичное программирования, элементы теории игр, динамические и стохастические задачи.

Переход к оптимизационной модели.

Нужны количественные характеристики элементов системы.

X1 ,…, X14 – переменные, значениями которых будут в соответствии с таблицей 2 либо вес соответствующей детали, либо сила воздействия.

Xi = Fij(Xj) – функция, описывающая связь соответствующих переменных, Gi - ограничения на допустимые значения i-ой переменной.

Если известны Xi = Fij(Xj) для всех пар (i, j) в соответствии с таблицей 2 ( - где есть связь) и множества Gi, то задача нахождения минимального веса велосипеда сводится к нахождению

минимума Xn,

Xn является сложной функцией – если подставить все зависимости Xi = Fij(Xj) в соответствии со всеми парами (i, j), где есть связь по таблице 2.

Должны выполняться условия: Xi принадлежит Gi, i=1,..., 14

Частные случаи относительно простого описания связей в подобных задачах построения моделей систем - Балансовые модели – в основе законы сохранения, равенство входа и выхода, баланс сил, равновесие производства и потребления, и т. п.

Пример балансовой модели

Есть производство из 5 участков, каждый участок производит продукцию и потребляет возможно свою, возможно других участков. Связь участков по потреблению задана матрицей - в заголовке столбца указан производитель, в строках потребители:

6 – это выходная продукция производства (внешняя связь) – 3, 4, 5 участки работают на выходную продукцию.

Каждый участок производит Хi единиц продукции, при i = 6, 7, 8 – это значение выходных переменных – продукция производства.

Пусть Aij – часть единицы продукции i – ого участка, которая необходима для производства единицы продукции j-ого участка (Aij. =0 если в соответствующей клетке матрицы ничего нет, ∑ Aij = 1 для j=1,… , 5). Тогда функционирование участка описывается балансовыми уравнениями:

Количество продукции i-ого участка Хi= ∑ Aij Хj, для всех i.

Если Aij известны, то это линейная система уравнений.

Выпуск задается.

Пусть нужно обеспечить выпуск: 100, 60, 20 единиц (здесь не оптимизация, а заданная величина выпуска).

Пусть заданы коэффициенты:

Система имеет вид:

Х1 = 0,25 Х1 + 0,25 Х2 + 0,5 Х5

Х2 = 0,75 Х1 + 0,125 Х4

Х3 = 0,625 Х4 + 100

Х4 = 0,75 Х2 + 0,25 Х5 + 60

Х5 = 0,25 Х4 + 0,25 Х5 + 20

Получаем решение: 80, 80, 160, 160, 80

Эта модель может быть рассмотрена и как динамическая, если считать Х функцией времени. Производство зависит от того, что произведено в предыдущие моменты времени. Уравнения можно переписать:

Хi (t + 1) = ∑ Aij Хj (t) если считать, что производство занимает 1 времени на всех участках, если иначе, то модель еще усложниться, но зато можно рассмотреть результат производства как функцию времени. Можно считать время дискретным тогда:

Хi (k + 1) = ∑ Aij Хj (k) где k= 0, … .

Для одной и той же системы можно построить много моделей.

Можно рассмотреть задачу о максимизации суммы

Х6 + Х7 + Х8 - хотим получить как можно больше продукции.

при условиях Хi= ∑ Aij Хj i=1, 2, 3, 4, 5

Хi > 0 i=1, 2, 3, 4, 5, 6, 7, 8

Это уже пример одной из наиболее изученных задач оптимизации – задачи линейного программирования (ЗЛП – подробнее будет рассмотрена ниже)

Тема 13. Применение метода экспертных оценок. Процедура многомерного выбора

Часто встречается задача, когда необходимо выбрать лучший объект из нескольких при условии, что существует набор критериев их оценки или объекты оцениваются несколькими экспертами.

Одним из решений такой задачи является формирование многомерной шкалы оценки объектов. При использовании таких шкал можно однозначно упорядочить объекты по степени их «хорошести, полезности». Необходимым условием для этого является сопоставимость свойств этих объектов.

Однако, широко распространены ситуации, в которых невозможно свести оценки объектов к одной. Противоречивость критериев имеет существенное значение: преимущества, получаемые по одному критерию, могут вызвать нежелательные изменения по другому критерию и при этом могут быть в принципе не соизмеримы.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14