Моделирование процессов и систем

Оглавление

1. Основы моделирования систем.. 4

1.1. Модели и моделирование. 4

1.2. Прикладные аспекты моделирования. 14

1.3. Основные свойства модели и моделирования. 16

2. Математическое и компьютерное моделирование. 19

2.1. Классификация видов моделирования. 19

2.2. Математическое моделирование сложных систем.. 21

2.3. Имитация случайных величин и процессов. 25

2.4. Основы математического моделирования. 27

2.5. Компьютерное моделирование. 32

3. Эволюционное моделирование и генетические алгоритмы.. 39

3.1. Основные атрибуты эволюционного моделирования. 39

3.3. Генетические алгоритмы.. 45

4. Генерирование случайных последовательностей. 48

4.1. Генерирование равномерно распределенных случайных чисел. 48

4.2. Основные критерии проверки случайных наблюдений. 56

4.3. Эмпирические критерии. 60

4.4. Численные распределения. 63

4.5. Признаки случайной последовательности. 67

5. Статистическое моделирование. 69

5.1. Введение. 69

5.2. Нормальное распределение. 70

5.3. Оценка максимального правдоподобия. 73

5.4. Метод наименьших квадратов. 74

6. Цепи Маркова. 77

6.1. Марковский процесс с дискретным временем.. 78

6.2. Марковские случайные процессы с непрерывным временем.. 87

6.3. Математический аппарат теории цепей Маркова. 91

6.4. Типовые задачи применения цепей Маркова. 93

6.5. Определение матрицы M среднего времени перехода. 97

7. Каноническое разложение случайного процесса. 104

7.1. Теоретические сведения. 104

7.2. Каноническое разложение случайного процесса в задачах. 105

8. Идентификация динамических объектов. 108

8.1. Общие положения идентификации математических моделей. 108

8.2. Обобщенная процедура идентификации. 109

9. Задачи детерминированного линейного оптимального управления. 120

9.1. Теоретические сведения. 120

9.2. Решение задач управления с применением уравнения Риккати. 121

10. Общие принципы построения моделирующих алгоритмов. 134

10.1. Принцип Δt. 135

10.2. Принцип особых состояний. 140

10.3. Принцип последовательной проводки заявок. 142

10.5. Объектный принцип моделирования. 147

11. Имитация случайных процессов. 149

11.1. Имитация нестационарных случайных процессов. 149

11.2. Имитация стационарных СП.. 150

11.3. Имитация стационарных нормальных СП.. 151

12. Обработка результатов моделирования. 153

12.1. Оценка вероятности. 153

12.2. Оценка математического ожидания и дисперсии. 154

12.3. Оценка характеристик случайного процесса. 154

12.4. Количество реализаций, обеспечивающих заданную точность. 155

13. Стохастическое линейное оптимальное регулирование. 157

13.1.Теоретические основы стохастического регулирования. 157

13.2. Решение задач стохастического линейного оптимального регулирования. 159

Литература. 166

1.  Основы моделирования систем

1.1. Модели и моделирование

Модель и моделирование - универсальные понятия, атрибуты одного из наиболее мощных методов познания в любой профессиональной области, познания системы, процесса, явления.

Вид модели и методы ее исследования больше зависят от информационно - логических связей элементов и подсистем моделируемой системы, ресурсов, связей с окружением, а не от конкретного наполнения системы.

Модельный стиль мышления позволяет вникать в структуру и внутреннюю логику моделируемой системы.

Построение модели - системная задача, требующая анализа и синтеза исходных данных, гипотез, теорий, знаний специалистов. Системный подход позволяет не только построить модель реальной системы, но и использовать эту модель для оценки (например, эффективности управления или функционирования) системы.

Модель - это объект или описание объекта, системы для замещения одной системы (оригинала) другой системой для лучшего изучения оригинала или воспроизведения каких-либо его свойств.

Например, отображая физическую систему на математическую систему, получим математическую модель физической системы. Любая модель строится и исследуется при определенных допущениях, гипотезах.

Пример. Рассмотрим физическую систему: тело массой m скатывается по наклонной плоскости с ускорением a, на которое воздействует сила F.

Исследуя такие системы, Ньютон получил математическое соотношение: F = m*a. Это физико-математическая модель системы или математическая модель физической системы скатывающегося тела.

При описании этой системы приняты следующие гипотезы:

·  поверхность идеальна (коэффициент трения равен нулю);

·  тело находится в вакууме (сопротивление воздуха равно нулю);

·  масса тела неизменна;

·  тело движется с одинаковым постоянным ускорением в любой точке.

Пример. Физиологическая система (система кровообращения человека) - подчиняется некоторым законам термодинамики. Описывая эту систему на физическом (термодинамическом) языке балансовых законов, получим физическую, термодинамическую модель физиологической системы. Если записать эти законы на математическом языке, т. е. соответствующие термодинамические уравнения, то уже получаем математическую модель системы кровообращения.

Пример. Совокупность предприятий функционирует на рынке, обмениваясь товарами, сырьем, услугами, информацией. Если описать экономические законы, правила их взаимодействия на рынке с помощью математических соотношений, например, системы алгебраических уравнений, где неизвестными будут величины прибыли, получаемые от взаимодействия предприятий, а коэффициентами уравнения будут значения интенсивностей таких взаимодействий, то получим экономико-математическую модель системы предприятий на рынке.

Слово "модель" (лат. modelium) означает "мера", "способ", "сходство с какой-то вещью".

Моделирование базируется на математической теории подобия, согласно которой абсолютное подобие может иметь место лишь при замене одного объекта другим точно таким же.

При моделировании большинства систем абсолютное подобие невозможно, и основная цель моделирования заключается в том, что модель достаточно хорошо должна отображать функционирование моделируемой системы.

По уровню, "глубине" моделирования модели бывают:

·  эмпирические - на основе эмпирических фактов (опытов);

·  теоретические - на основе математических описаний;

·  смешанные, полуэмпирические - на основе эмпирических зависимостей и математических описаний.

Проблема моделирования состоит из трех задач:

·  построение модели (эта задача менее формализуема и конструктивна, т. к. нет алгоритма для построения моделей);

·  исследование модели (эта задача более формализуема, имеются методы исследования различных классов моделей);

·  использование модели (конструктивная и конкретизируемая задача).

Модель М, описывающая систему S(x1, x2, ..., xn; R), имеет вид:

М = (z1, z2, ..., zm; Q), где zi Z, (i = 1, 2, ..., n);

R - множества отношений над X;

Q - множества отношений над Z;

Х - множеством входных, выходных сигналов и состояний системы;

Z - множество описаний (представлений) элементов и подмножеств X.

Схема построения модели М системы S с входными сигналами X и выходными сигналами Y изображена на рис. 1.1.

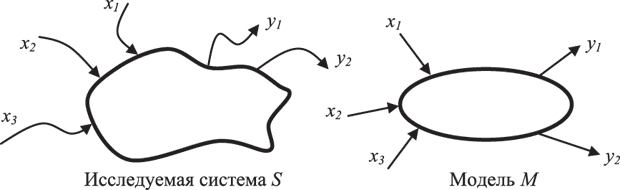
Рис. 1.1.  Схема построения модели

Если на вход М поступают сигналы из X и на выходе появляются сигналы Y, то задан закон (правило) f функционирования модели / системы.

Моделирование - это универсальный метод получения описания функционирования объекта и использования знаний о нем. Моделирование используется в любой профессиональной деятельности

Классификацию моделей проводят по различным критериям.

Модель называется статической, если среди параметров, участвующих в ее описании, нет временного параметра. Статическая модель в каждый момент времени дает лишь "фотографию" системы, ее срез.

Пример. Закон Ньютона F=a*m - это статическая модель движущейся с ускорением a материальной точки массой m. Эта модель не учитывает изменение ускорения от одной точки к другой.

Модель динамическая, если среди ее параметров есть временной параметр, т. е. она отображает систему (процессы в системе) во времени.

Пример. Динамическая модель закона Ньютона будет иметь вид:

F(t)=a(t)*m(t).

Модель дискретная, если она описывает поведение системы только в дискретные моменты времени.

Пример. Если рассматривать только t=0, 1, 2, …, 10 (сек), то модель

St=gt2/2

или числовая последовательность: S0=0, S1=g/2, S2=2g, S3=9g/2, :, S10=50g может служить дискретной моделью движения свободно падающего тела.

Модель непрерывная, если она описывает поведение системы для всех моментов времени некоторого промежутка времени.

Пример. Модель S=gt2/2, 0 < t < 100 непрерывна на промежутке времени (0;100).

Модель имитационная, если она предназначена для испытания или изучения возможных путей развития и поведения объекта путем варьирования некоторых или всех параметров модели.

Пример. Пусть модель экономической системы производства товаров двух видов 1 и 2, в количестве x1 и x2 единиц и стоимостью каждой единицы товара a1 и a2 на предприятии описана в виде соотношения:

a1x1 + a2x2 = S,

где S - общая стоимость произведенной предприятием всей продукции (вида 1 и 2). Можно ее использовать в качестве имитационной модели, по которой можно определять (варьировать) общую стоимость S в зависимости от тех или иных значений объемов и стоимости производимых товаров.

Модель детерминированная, если каждому входному набору параметров соответствует вполне определенный и однозначно определяемый набор выходных параметров; в противном случае - модель недетерминированная, стохастическая (вероятностная).

Пример. Приведенные выше физические модели - детерминированные. Если в модели S = gt2 / 2, 0 < t < 100 мы учли бы случайный параметр - порыв ветра с силой p при падении тела:

S(p) = g(p) t2 / 2, 0 < t < 100,

то мы получили бы стохастическую модель (уже не свободного) падения.

Модель функциональная, если она представима в виде системы каких - либо функциональных соотношений.

Модель теоретико-множественная, если она представима с помощью некоторых множеств и отношений принадлежности им и между ними.

Пример. Пусть задано множество

X = {Николай, Петр, Николаев, Петров, Елена, Екатерина, Михаил, Татьяна} и отношения:

·  Николай - супруг Елены,

·  Екатерина - супруга Петра,

·  Татьяна - дочь Николая и Елены,

·  Михаил - сын Петра и Екатерины,

·  семьи Михаила и Петра дружат друг с другом.

Тогда множество X и множество перечисленных отношений Y могут служить теоретико-множественной моделью двух дружественных семей.

Модель называется логической, если она представима предикатами, логическими функциями.

Например, совокупность логических функций вида:

z = x 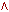y x, p = x y

есть математическая логическая модель работы дискретного устройства.

Модель игровая, если она описывает, реализует некоторую игровую ситуацию между участниками игры.

Пример. Пусть игрок 1 - добросовестный налоговый инспектор, а игрок 2 - недобросовестный налогоплательщик. Идет процесс (игра) по уклонению от налогов (с одной стороны) и по выявлению сокрытия уплаты налогов (с другой стороны). Игроки выбирают натуральные числа i и j (i, j n), которые можно отождествить, соответственно, со штрафом игрока 2 за неуплату налогов при обнаружении игроком 1 факта неуплаты и с временной выгодой игрока 2 от сокрытия налогов. Если в качестве модели взять матричную игру с матрицей выигрышей порядка n, то в ней каждый элемент определяется по правилу aij = |i - j|. Модель игры описывается этой матрицей и стратегией уклонения и поимки. Эта игра - антагонистическая.

Модель алгоритмическая, если она описана некоторым алгоритмом или комплексом алгоритмов, определяющим функционирование, развитие системы.

Cледует помнить, что не все модели могут быть исследованы или реализованы алгоритмически.

Пример. Моделью вычисления суммы бесконечного убывающего ряда чисел может служить алгоритм вычисления конечной суммы ряда до некоторой заданной степени точности. Алгоритмической моделью корня квадратного из числа x может служить алгоритм вычисления его приближенного значения по известной рекуррентной формуле.

Модель называется структурной, если она представима структурой данных или структурами данных и отношениями между ними.

Модель называется графовой, если она представима графом или графами и отношениями между ними.

Модель называется иерархической (древовидной), если представима некоторой иерархической структурой (деревом).

Пример. Для решения задачи нахождения маршрута в дереве поиска можно построить, например, древовидную модель (рис. 1.2):

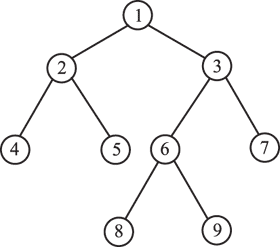
Рис. 1.2.  Модель иерархической структуры

Модель называется сетевой, если она представима некоторой сетевой структурой.

Пример. Строительство нового дома включает операции, приведенные в нижеследующей таблице.

Сетевая модель (сетевой график) строительства дома дана на рис. 1.3.

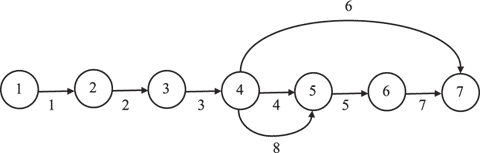
Рис. 1.3.  Сетевой график строительства работ

Две работы, соответствующие дуге 4-8, параллельны, их можно либо заменить одной, представляющей совместную операцию (монтаж электропроводки и настил крыши) с новой операцией длительностью 3+5=8, либо ввести на одной дуге фиктивное событие.

Модель называется языковой, лингвистической, если она представлена некоторым лингвистическим объектом, формализованной языковой системой или структурой.

Иногда такие модели называют вербальными, синтаксическими.

Например, правила дорожного движения - языковая, структурная модель движения транспорта и пешеходов на дорогах.

Пусть B - множество производящих основ существительных, C - множество суффиксов, P - прилагательных, bi – корень слова; "+" - операция конкатенации слов, ":=" - операция присваивания, "=>" - операция вывода (выводимости новых слов), Z - множество значений (смысловых) прилагательных.

Языковая модель M словообразования может быть представлена:

<pi> = <bi> + <сi>.

При bi - "рыб(а)", сi - "н(ый)", получаем по этой модели pi - "рыбный", zi - "приготовленный из рыбы".

Модель визуальная, если она позволяет визуализировать отношения и связи моделируемой системы, особенно в динамике.

Например, на экране компьютера часто пользуются визуальной моделью того или иного объекта.

Модель натурная, если она есть материальная копия объекта моделирования.

Например, глобус - натурная географическая модель земного шара.

Модель геометрическая, графическая, если она представима геометрическими образами и объектами.

Например, макет дома является натурной геометрической моделью строящегося дома. Вписанный в окружность многоугольник дает модель окружности. Именно она используется при изображении окружности на экране компьютера. Прямая линия является моделью числовой оси, а плоскость часто изображается, как параллелограмм.

Модель клеточно-автоматная, если она представима клеточным автоматом или системой клеточных автоматов.

Клеточный автомат - дискретная динамическая система, аналог физического (непрерывного) поля. Клеточно-автоматная геометрия - аналог евклидовой геометрии. Неделимый элемент евклидовой геометрии - точка, на основе ее строятся отрезки, прямые, плоскости и т. д.

Неделимый элемент клеточно-автоматного поля - клетка, на основе её строятся кластеры клеток и различные конфигурации клеточных структур. Представляется клеточный автомат равномерной сетью клеток ("ячеек") этого поля. Эволюция клеточного автомата разворачивается в дискретном пространстве - клеточном поле.

Смена состояний в клеточно-автоматном поле происходит одновременно и параллельно, а время идет дискретно. Несмотря на кажущуюся простоту их построения, клеточные автоматы могут демонстрировать разнообразное и сложное поведение объектов, систем.

В последнее время они широко используются при моделировании не только физических, но и социально-экономических процессов.

1.2. Прикладные аспекты моделирования

Модель называется фрактальной, если она описывает эволюцию моделируемой системы эволюцией фрактальных объектов.

Если физический объект однородный (сплошной), т. е. в нем нет полостей, то можно считать, что его плотность не зависит от размера. Например, при увеличении параметра объекта R до 2R масса объекта увеличится в R2 раз, если объект - круг и в R3 раз, если объект - шар, т. е. существует связь массы и длины. Пусть n - размерность пространства. Объект, у которого масса и размер связаны называется "компактным". Его плотность можно рассчитать по формуле:

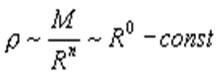
Если объект (система) удовлетворяет соотношению M(R) ~ Rf(n), где f(n) < n, то такой объект называется фрактальным.

Его плотность не будет одинаковой для всех значений R, то она масштабируется согласно формуле:

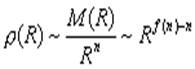
Так как f(n) - n < 0 по определению, то плотность фрактального объекта уменьшается с увеличением размера R, а ρ(R) является количественной мерой разряженности объекта.

Пример фрактальной модели - множество Кантора. Рассмотрим отрезок [0;1]. Разделим его на 3 части и выбросим средний отрезок. Оставшиеся 2 промежутка опять разделим на три части и выкинем средние промежутки и т. д. Получим множество, называемое множеством Кантора. В пределе получаем несчетное множество изолированных точек (рис. 1.4)

Рис. 1.4.  Множество Кантора для 3-х делений

1.3. Основные свойства модели и моделирования

Границы между моделями различного вида весьма условны. Можно говорить о различных режимах использования моделей - имитационном, стохастическом, динамическом, детерминированном и др.

Как правило, модель включает в себя: объект О, субъект А (не обязательно) , задачу Z, ресурсы B, среду моделирования С.

Модель можно представить формально в виде: М = < O, А, Z, B, C >.

Основные свойства любой модели:

целенаправленность - модель всегда отображает некоторую систему, т. е. имеет цель такого отображения; конечность - модель отображает оригинал лишь в конечном числе его отношений и ресурсы моделирования конечны; упрощенность - модель отображает только существенные стороны объекта и она должна быть проста для исследования или воспроизведения; наглядность, обозримость основных ее свойств и отношений; доступность и технологичность для исследования или воспроизведения; информативность - модель должна содержать достаточную информацию о системе (в рамках гипотез, принятых при построении модели) и должна давать возможность получать новую информацию; полнота - в модели должны быть учтены все основные связи и отношения, необходимые для обеспечения цели моделирования; управляемость - модель должна иметь хотя бы один параметр, изменениями которого можно имитировать поведение моделируемой системы в различных условиях.

Жизненный цикл моделируемой системы:

сбор информации об объекте, выдвижение гипотез, предварительный модельный анализ; проектирование структуры и состава моделей (подмоделей); построение спецификаций модели, разработка и отладка отдельных подмоделей, сборка модели в целом, идентификация (если это нужно) параметров моделей; исследование модели - выбор метода исследования и разработка алгоритма (программы) моделирования; исследование адекватности, устойчивости, чувствительности модели; оценка средств моделирования (затраченных ресурсов); интерпретация, анализ результатов моделирования и установление некоторых причинно-следственных связей в исследуемой системе; генерация отчетов и проектных (народно-хозяйственных) решений; уточнение, модификация модели, если это необходимо, и возврат к исследуемой системе с новыми знаниями, полученными с помощью модели и моделирования.

Моделирование – есть метод системного анализа.

Часто в системном анализе при модельном подходе исследования может совершаться одна методическая ошибка, а именно, - построение корректных и адекватных моделей (подмоделей) подсистем системы и их логически корректная увязка не дает гарантий корректности построенной таким способом модели всей системы.

Модель, построенная без учета связей системы со средой, может служить подтверждением теоремы Геделя, а точнее, ее следствия, утверждающего, что в сложной изолированной системе могут существовать истины и выводы, корректные в этой системе и некорректные вне ее.

Наука моделирования состоит в разделении процесса моделирования (системы, модели) на этапы (подсистемы, подмодели), детальном изучении каждого этапа, взаимоотношений, связей, отношений между ними и затем эффективного описания их с максимально возможной степенью формализации и адекватности.

В случае нарушения этих правил получаем не модель системы, а модель "собственных и неполных знаний".

Моделирование рассматривается, как особая форма эксперимента, эксперимента не над самим оригиналом, т. е. простым или обычным экспериментом, а над копией оригинала. Здесь важен изоморфизм систем оригинальной и модельной.

Изоморфизм - равенство, одинаковость, подобие.

Модели и моделирование применяются по основным направлениям:

в обучении, в познании и разработке теории исследуемых систем; в прогнозировании (выходных данных, ситуаций, состояний системы); в управлении (системой в целом, отдельными ее подсистемами); в автоматизации (системы или ее отдельных подсистем).

2.  Математическое и компьютерное моделирование

2.1. Классификация видов моделирования

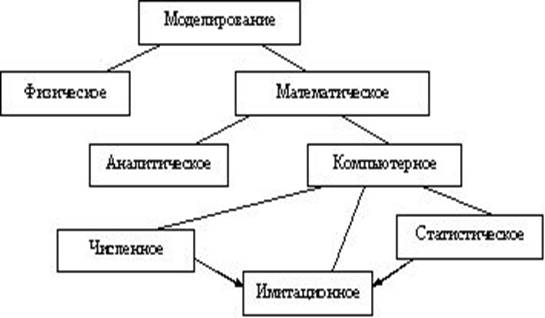
Рис. 2.1. Классификация видов моделирования

При физическом моделировании используется сама система, либо подобная ей в виде макета, например, летательный аппарат в аэродинамической трубе.

Математическое моделирование есть процесс установления соответствия реальной системе S математической модели M и исследование этой модели, позволяющее получить характеристики реальной системы.

При аналитическом моделировании процессы функционирования элементов записываются в виде математических соотношений (алгебраических, интегральных, дифференциальных, логических и др.).

Аналитическая модель может быть исследована методами:

·  аналитическими (устанавливаются явные зависимости, получаются, в основном, аналитические решения);

·  численными (получаются приближенные решения);

Компьютерное математическое моделирование формулируется в виде алгоритма (программы для ЭВМ), что позволяет проводить над моделью вычислительные эксперименты.

Численное моделирование использует методы вычислительной математики.

Статистическое моделирование использует обработку данных о системе с целью получения статистических характеристик системы.

Имитационное моделирование воспроизводит на ЭВМ (имитирует) процесс функционирования исследуемой системы, соблюдая логическую и временную последовательность протекания процессов, что позволяет узнать данные о состоянии системы или отдельных ее элементов в определенные моменты времени.

Применение математического моделирования позволяет исследовать объекты, реальные эксперименты над которыми затруднены или невозможны.

Экономический эффект при математическом моделировании состоит в том, что затраты на проектирование систем в среднем сокращаются в 50 раз.

2.2. Математическое моделирование сложных систем

Будем считать, что элемент s есть некоторый объект, обладающий определенными свойствами, внутреннее строение которого для целей исследования не играет роли, например, самолет для моделирования полета – не элемент, а для моделирования работы аэропорта – элемент.

Связь l между элементами есть процесс их взаимодействия, важный для целей исследования.

Система S – совокупность элементов со связями и целью функционирования F.

Сложная система – это система, состоящая из разнотипных элементов с разнотипными связями.

Большая система – это система, состоящая из большого числа однотипных элементов с однотипными связями.

В общем виде систему математически можно представить в виде:

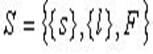
Автоматизированная система SA есть сложная система с определяющей ролью элементов двух типов: технических средств Sт и действий человека SH:

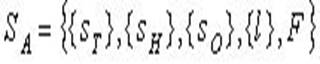
Здесь s0 - остальные элементы системы.

Декомпозиция системы есть разбиение системы на элементы или группы элементов с указанием связей между ними, неизменными во время функционирования системы.

Практически все системы рассматриваются функционирующими во времени, поэтому определим их динамические характеристики.

Состояние – это множество характеристик элементов системы, изменяющихся во времени и важных для целей ее функционирования.

Процесс (динамика) – это множество значений состояний системы, изменяющихся во времени.

Цель функционирования есть задача получения желаемого состояния системы. Достижение цели обычно влечет целенаправленное вмешательство в процесс функционирования системы, которое называется управлением.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8