Рассмотрим подход с использованием меры по Н. Моисееву.

Пусть дана некоторая управляемая система, о состояниях которой известны лишь некоторые оценки - нижняя smin и верхняя smax. Известна целевая функция управления

F( s(t), u(t) ),

где s(t) - состояние системы в момент времени t, а u(t) - управление из некоторого множества допустимых управлений, причем считаем, что достижимо uopt - некоторое оптимальное управление в пространстве U,

t0 < t < T, smin s smax.

Мера успешности принятия решения может быть выражена математически:

H = |(Fmax - Fmin) / (Fmax + Fmin)|,

Fmax = max F(uopt, smax), Fmin = min F(uopt, smin),

t [ t 0; T ], s [ smin; smax ].

Увеличение Н свидетельствует об успешности управления системой.

Функции управления должны отражать эволюцию системы, в частности, удовлетворять условиям:

1.  Периодичности (цикличности), например:

( 0 < T < ∞, t: 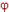 (i)(s; s(i), t) =  (i)(s; s(i), t + T),

 (i)(s; s(i), t) =   (i)(s; s(i), t + T)).

2.  Затуханию при снижении активности, например:

(s(x) 0 i = 1, 2, ..., n) => ( (i) 0,  (i)  0).

3.  Стационарности: выбор или определение функций (i), (i) осуществляется таким образом, чтобы система имела точки равновесного состояния, а s(i)opt, sopt достигались бы в стационарных точках x(i)opt, xopt для малых промежутков времени. В больших промежутках времени система может вести себя хаотично, самопроизвольно порождая регулярные, упорядоченные, циклические взаимодействия (детерминированный хаос).

Взаимные активности (ij) ( s; s(i), s(j), t) подсистем i и j не учитываются. В качестве функций (i), (i) могут быть использованы некоторые известные производственные функции.

Обратимся к социально - экономической среде, которая может возобновлять с коэффициентом возобновления

(τ, t, x) (0 < t <T, 0 < x < 1, 0 < τ < T)

свои ресурсы. Этот коэффициент зависит от мощности среды (ресурсоемкости и ресурсообеспеченности).

Рассмотрим простую гипотезу:

(τ, t, x) =  0 + 1x,

Чем больше ресурсов - тем больше темп их возобновления.

Отметим, что если ds/dt - общее изменение энтропии системы, ds1/dt - изменение энтропии за счет необратимых изменений структуры, потоков внутри системы, ds2/dt - изменение энтропии за счет усилий по улучшению обстановки (например, экономической, экологической, социальной), то справедливо уравнение И. Пригожина:

ds/dt = ds1/dt + ds2/dt.

При эволюционном моделировании социально - экономических систем полезно использовать как классические математические модели, так и неклассические, в частности, учитывающие пространственную структуру системы, структуру и иерархию подсистем (графы, структуры данных и др.), опыт и интуицию (эвристические, экспертные процедуры).

Пример. Пусть дана некоторая экологическая система Ω, в которой имеются точки загрязнения (выбросов загрязнителей) xi, i = 1, 2, …, n. Каждый загрязнитель xi загрязняет последовательно экосистему в промежутке времени [ ti-1; ti ]. Каждый загрязнитель может оказать воздействие на активность другого загрязнителя (например, уменьшить, нейтрализовать или усилить по известному эффекту суммирования воздействия загрязнителей). Силу (меру) такого влияния можно определить через rij,

R = {rij: i = 1, 2,…, n-1; j = 2, 3,…, n}.

Структура задаётся графом: вершины - загрязнители, ребра – меры загрязнения. Рассмотрим функционал вида:

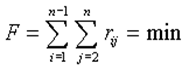
где F - суммарное загрязнение системы данной структуры S.

Чем быстрее будет произведен учёт загрязнения в точке xi, тем быстрее осуществимы социально - экономические мероприятия по его нейтрализации. Чем меньше будет загрязнителей до загрязнителя xi, тем меньше будет загрязнение среды.

Принцип эволюционного моделирования предполагает необходимость и эффективность использования методов и технологии искусственного интеллекта, в частности, экспертных систем.

Адекватным средством реализации процедур эволюционного моделирования являются генетические алгоритмы.

3.3. Генетические алгоритмы

Идея генетических алгоритмов "подсмотрена" у систем живой природы, у которых эволюция развертывается достаточно быстро.

Генетический алгоритм - это алгоритм, основанный на имитации генетических процедур развития популяции в соответствии с принципами эволюционной динамики.

Генетические алгоритмы используются для решения задач оптимизации (многокритериальной), для задач поиска и управления.

Данные алгоритмы адаптивны, они развивают решения и развиваются сами.

Пример. Рассмотрим задачу безусловной целочисленной оптимизации (размещения): найти максимум функции f(i), i - набор из n нулей и единиц, например, при n = 5, i = (1, 0, 0, 1, 0). Это очень сложная комбинаторная задача для обычных, "негенетических" алгоритмов. Генетический алгоритм может быть построен на основе следующей укрупненной процедуры:

1.  Генерируем начальную популяцию (набор допустимых решений задачи) I0 = (i1, i2, :, in), ij {0,1} и определяем некоторый критерий достижения "хорошего" решения, критерий остановки, процедуру СЕЛЕКЦИЯ, процедуру СКРЕЩИВАНИЕ, процедуру МУТАЦИЯ и процедуру обновления популяции ОБНОВИТЬ;

2.  k = 0, f0 = max{f(i), i I0};

3.  выполнять пока не :

·  с помощью вероятностного оператора (селекции) выбираем два допустимых решения (родителей) i1, i2 из выбранной популяции (вызов процедуры СЕЛЕКЦИЯ);

·  по этим родителям строим новое решение (вызов процедуры СКРЕЩИВАНИЕ) и получаем новое решение i;

·  модифицируем это решение (вызов процедуры МУТАЦИЯ);

·  если f0 < f(i) то f0 = f(i);

·  обновляем популяцию (вызов процедуры ОБНОВИТЬ);

·  k = k + 1

Подобные процедуры определяются с использованием аналогичных процедур живой природы.

Процедура СЕЛЕКЦИЯ может из случайных элементов популяции выбирать элемент с наибольшим значением f(i).

Процедура СКРЕЩИВАНИЕ (кроссовер) может по векторам i1, i2 строить вектор i, присваивая с вероятностью 0.5 соответствующую координату каждого из этих векторов - родителей. Это самая простая процедура. Используют и более сложные процедуры, реализующие более полные аналоги генетических механизмов.

Процедура МУТАЦИЯ так же может быть простой или сложной. Например, простая процедура с задаваемой вероятностью для каждого вектора меняет его координаты на противоположные (0 на 1, и наоборот).

Процедура ОБНОВИТЬ заключается в обновлении всех элементов популяции в соответствии с указанными процедурами.

Хотя генетические алгоритмы и могут быть использованы для решения задач, которые, нельзя решить другими методами, они не гарантируют нахождение оптимального решения, по крайней мере, за приемлемое время. Здесь более уместны критерии типа "достаточно хорошо и достаточно быстро".

Главное же преимущество их использования заключается в том, что они позволяют решать сложные задачи, для которых не разработаны пока устойчивые и приемлемые методы, особенно на этапе формализации и структурирования системы.

Генетические алгоритмы эффективны в комбинации с другими классическими алгоритмами и эвристическими процедурами.

4. Генерирование случайных последовательностей

4.1. Генерирование равномерно распределенных случайных чисел

«Каждый, кто использует арифметические методы генерирования случайных чисел, безусловно, грешит».

Джон фон Нейман

Числа, которые выбираются случайным образом, находят множество полезных применений:

·  моделирование. Это позволяет сделать модели похожими на реальные явления;

·  выборочный метод. Часто невозможно исследовать все варианты, но случайная выборка обеспечивает понимание того, что можно назвать «типичным поведением»;

·  численный анализ. Для решения сложных задач численного анализа была разработана техника, использующая случайные числа;

·  компьютерное программирование. Случайные числа являются хорошим источником данных для тестирования эффективности компьютерных алгоритмов;

·  принятие решений;

·  эстетика;

·  развлечения.

Равномерным распределением на конечном множестве чисел называется такое распределение, при котором любое из возможных чисел имеет одинаковую вероятность появления. Если не задано определенное распределение на конечном множестве чисел, то принято считать его равномерным [3].

Джон фон Нейман первым предложил в 1946 г. идею возвести в квадрат случайное число и выделить из него средние цифры. Например, необходимо получить новое десятизначное число по числу . Возводим имеющееся число в квадрат и выделяем средние 10 цифр:

.

Новым сгенерированным числом будет число . Претензии к такому подходу касаются вопроса: как может быть случайной последовательность, генерируемая таким образом, если каждое число полностью определяется предыдущим? Ответ состоит в том, что эта последовательность не случайна, но кажется такой. Последовательности, генерируемые детерминистическим путем, таким как этот, называются псевдослучайными или квазислучайными.

Метод середины квадратов фактически является сравнительно бедным источником случайных чисел. Опасность состоит в коротком цикле (периоде) повторяющихся элементов. Рассмотрим методы генерирования последовательности случайных дробей [3], т. е. случайных действительных чисел Un, равномерно распределенных между нулем и единицей. Будем генерировать целое число Хn между нулем и некоторым числом U, тогда дробь при m >= U

Un = Хn / m

будет принадлежать [0,1]. Обычно m выбирают равным размеру компьютерного слова. Обозначим m = be, где b — основание системы счисления, используемой ЭВМ, а e — число разрядов машины. Поэтому Хn можно по традиции рассматривать как целое число, занимающее все компьютерное слово с точкой в правом конце слова, а Un — как содержимое того же слова с точкой в левом конце слова.

Линейный конгруэнтный метод

Выберем четыре числа [3]:

m — модуль, m > 0;

a — множитель, 0 £ a < m;

c — приращение, 0 £ с < m;

Х0 — начальное значение, 0 £ Х0 < m.

Последовательность случайных чисел {Хn} можно получить, полагая

Хn+1 = (a Хn + c) mod m, n ³ 0 , (4.1)

где mod – операция взятия остатка от деления. Последовательность (4.1) называется линейной конгруэнтной последовательностью. Например, для m = 10 и Х0 = a = c = 7 получим последовательность

7, 6, 9, 0, 7, 6, 9, 0, 7…

В примере отражен факт, что конгруэнтная последовательность всегда образует петли, т. е. обязательно существует цикл, повторяющийся бесконечное число раз. Это свойство является общим для всех последовательностей вида Xn+1 = f(Xn), где f — функция, преобразующая конечное множество само в себя. Повторяющиеся циклы называют периодами. Задача генерации случайных последовательностей состоит в использовании относительно длинного периода, что связано с выбором довольно большого m, так как период не может иметь больше m элементов. Другой фактор — скорость генерирования. При выборе множителя а следует принимать во внимание выводы следующей теоремы.

Линейная конгруэнтная последовательность, определенная числами m, a, c и X0, имеет период длиной m тогда и только тогда, когда:

·  числа с и m взаимно простые;

·  b = a - 1 кратно p для каждого простого p, являющегося делителем m;

·  b кратно 4, если m кратно 4.

Пример. Для m = 120 назначить а и построить последовательность случайных чисел в интервале [0,1].

Решение. Выберем с = 7, a = 5, тогда при x0 = 1 получим следующие числа: X1 = 12, X2 = 67, X3 = 102, … Далее генерируем u0 = 1/120, u1 = 12/120, u2 = 67/120, u3 = 102/120, …

В связи с довольно простым получением случайных чисел возникает такая общепринятая ошибочная идея — достаточно взять хороший генератор случайных чисел и немного его модифицировать для того, чтобы получить «еще более случайную» последовательность. Часто это не так. Например, известно, что формула (4.1) позволяет получить более или менее хорошие случайные числа. Может ли последовательность, полученная из

Xn+1 = ((a Xn) mod (m + 1) + c) mod m

быть еще более случайной? Ответ: новая последовательность является менее случайной с большей долей вероятности, т. е. мы попадаем в область генераторов типа Xn+1 = f(Xn) с выбранной произвольно функцией f. Доказано, что такие последовательности, ведут себя хуже, чем последовательности, полученные при использовании более регулярных функций (4.1).

Отметим, что период линейной конгруэнтной последовательности довольно длинный; когда m приблизительно равно длине слова компьютера, обычно получаются периоды порядка 109 или больше, а в типичных вычислениях используется лишь малая часть всей последовательности.

Рассмотрим аддитивный генератор, предложенный Дж. Ж. Митчелом и :

Xn = (Xn-24 + Xn-55) mod m, n ³ 55, (4.2)

где m — четное число, числа 24 и 55 — специальные числа, выбранные для того, чтобы определить такую последовательность, младшие значащие двоичные разряды (Xn mod  2) которой имеют длину периода 255 – 1.

(Аддитивный генератор чисел). В ячейки памяти Y[1], Y[2], …, Y[55] записано множество значений X54 , X53 , …, X0 соответственно; в начале полагают j = 24, k = 55.

При реализации этого алгоритма на выходе последовательно получаем числа X55, X56, …

В1. [Суммирование] (Если на выходе мы оказываемся в точке Xn, то

Y[j] = Xn-24, а Y[k] = Xn-55.

Y[k] (Y[k] + Y[j]) mod 2e.

В2. [Продвижение] Уменьшим j и k на 1. Если j = 0, то присвоим j 24, иначе, если k = 0, присвоить k 55.

Числа 24 и 55 в выражении (4.2) называются запаздыванием, а числа Xn, определенные в (4.2) — последовательностью Фибоначчи с запаздыванием.

Возможно построить достаточно хороший генератор случайных чисел, используя всевозможные линейные комбинации Xn-1, …, Xn-k для малых k. В этом случае наилучший результат получается, когда модуль m является большим простым числом; например, m - наибольшее простое число, которое можно записать одним компьютерным словом.

Формула для генерации может быть выбрана такой:

Xn = ( a1 Xn-1 + … + ak Xn-k ) mod p (4.3)

с периодом pk – 1. Здесь X0 , X1, …, Xk-1 могут быть выбраны произвольно, но не равные нулю одновременно.

Обратимся к процессу генерирования случайных чисел «0» и «1» по формуле (4.3). Зададим произвольно ненулевое двоичное слово, то есть X1 = 1, X2 = 0, X3 = 1, X4 = 1; k = 4; p = 2. Зададим произвольно коэффициенты а1, а2, а3, а4 двоичным словом, то есть а1 = 0, а2 = 0, а3 = 1, а4 = 1. Перепишем (4.3) с учетом введенных величин, получим:

Xn = (a1 ×Xn-1 + a2 ×Xn-2 + a3 ×Xn-3 + a4 × Xn-4 ) mod 2

Xn = (0 ×Xn-1 + 0 ×Xn-2 + 1 ×Xn-3 + 1 × Xn-4 ) mod 2

Xn = ( Xn-3 + Xn-4 ) mod 2.

Откуда следует, что

X5 = (X2 + X1) mod 2 = 1.

X6 = (X3 + X2) mod 2 = 1; X7 = (X4 + X3) mod 2 = 0;

X8 = (X5 + X4) mod 2 = 0; X9 = (X6 + X5) mod 2 = 0;

X10 = (X7 + X6) mod 2 = 1; X11 = (X8 + X7) mod 2 = 0;

X12 = (X9 + X8) mod 2 = 0; … и т. д.

Сгенерированные числа (коды) имеют значения:

1011 (начальное число); 1100; 0100; 1101; 0111; 1000; 1001 …

Период, т. е. число шагов, через которое начинается повтор, равняется 24 – 1 = 15.

Для генерирования случайных чисел предложено множество других схем. Наиболее интересным из альтернативных методов является обратная конгруэнтная последовательность, предложенная Эйченауэром и Лехном:

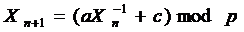(4.4)

Здесь p — простое число, Xn принимает значения из множества {0, 1, …, p-1, …¥}, а обращение определено как 0-1 = ¥, ¥-1 = 0. X-1 ×X º 1 по модулю p.

Другой важный класс методов связан с комбинацией генераторов случайных чисел.

Допустим, имеются последовательности X0 , X1, … и Y0 , Y1, … случайных чисел, лежащих между 0 и m–1 и предпочтительно сгенерированных двумя различными методами. Тогда можно использовать одну случайную последовательность для изменения порядка элементов другой. Рассмотрим алгоритм рандомизации перемешиванием.

Алгоритм М (рандомизации перемешиванием)

Если заданы методы генерирования двух последовательностей {Xn} и {Yn}, этот алгоритм будет последовательно генерировать элементы «значительно более случайной» последовательности. Воспользуемся вспомогательной таблицей V[0], V[1], …, V[k-1], где k — некоторое число, для удобства обычно выбираемое приблизительно равным 100. Вначале V - таблица заполняется первыми k значениями последовательности X.

М1. [Генерирование X, Y]. Положим X и Y равными следующим членам последовательности {Xn} и {Yn} соответственно.

М2. [Выбор j]. Присвоим j [k×Y/m], где m — модуль, используемый в последовательности{Yn}, т. е. j — случайная величина, определяемая Y, 0 £ j < k.

M3. [Замена]. Выведем V[j], а затем присвоим V[j] X.

Отметим, что методы перемешивания имеют «врожденный дефект». Они изменяют порядок следования генерируемых чисел, но не сами числа. Поэтому на практике возможно применение следующего подхода к генерации последовательности случайных чисел:

Zn = (Xn - Yn) mod m, (4.5)

где 0 £ Xn < m и 0 £ Yn < m¢ £ m.

Простейшим путем улучшения случайности при с = 0 является использование только каждого j - го элемента для некоторого малого j. Но лучшим способом, возможно, еще более простым, является применение (4.1) для получения скажем массива из 500 случайных чисел и использование только первых 55 чисел. После этого таким же методом генерируются следующие 55 чисел и т. д.

4.2. Основные критерии проверки случайных наблюдений

Статистические критерии [3] отвечают на вопрос: достаточно ли случайной будет последовательность. Если критерии T1 , T2, …, Tn подтверждают, что последовательность ведет себя случайным образом, это еще не означает, вообще говоря, что проверка с помощью Tn+1–го критерия будет успешной. Однако каждая успешная проверка дает больше оснований, подтверждающих случайность последовательности. Обычно к последовательности применяется несколько статистических критериев и, если она удовлетворяет этим критериям, то последовательность считается случайной.

Различают два вида статистических критериев: эмпирические и теоретические. Эмпирические критерии основаны на использовании определенных статистик. Теоретические критерии основаны на использовании теоретико-числовых методов.

Рассмотрим критерий «хи - квадрат» (c2-критерий) [3]. Он является основным эмпирическим критерием, используемым в сочетании с другими критериями. Прежде чем рассматривать идею в целом, проанализируем частный пример применения c2-критерия к бросанию игральной кости.

Используем 2 игральные кости, каждая из которых независимо допускает выпадение значений 1, 2, …, 6 с равной вероятностью. В следующей таблице дана вероятность получения определенной суммы S при одном бросании игральных костей:

Имеем всего 36 возможных результатов бросания. Рассмотрим результаты бросания. Например, величина 4 может быть получена тремя способами: 1 + 3, 2 + 2, 3 + 1. Это составляет 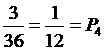. Аналогично определяются оставшиеся вероятности PS. Если бросать игральную кость n раз, то в среднем мы должны получить величину S примерно n × PS раз, но это не совсем так. Например, при 144 бросаниях были получены следующие результаты:

Таблица 4.1

Заметим, что во всех случаях наблюдаемое число отличается от ожидаемого. Введем в рассмотрение число :

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8