Задачи исследования систем:
1. Расчет - определение значений параметров системы.
2. Анализ – изучение свойств функционирования системы.
3. Синтез – выбор структуры и параметров по заданным свойствам системы.
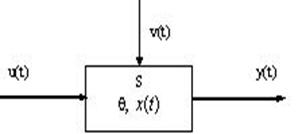
Пусть T = [t0, t1] есть временной интервал моделирования системы S (интервал модельного времени).
Построение модели начинается с определения параметров и переменных, определяющих процесс функционирования системы.
Параметры системы ![]() - это характеристики системы, остающиеся постоянными на всем интервале T.
- это характеристики системы, остающиеся постоянными на всем интервале T.
Переменные бывают зависимые и независимые.
Независимые переменные есть, как правило, входные воздействия (в том числе управляющие)
![]()
ими могут быть также воздействия внешней среды.
Последовательность изменения x(t) при
![]()
называется фазовой траекторией системы,![]() , где X – пространство состояний или фазовое пространство.
, где X – пространство состояний или фазовое пространство.
Последовательность изменения y(t) называется выходной траекторией системы.
Зависимые переменные есть выходные характеристики (сигналы)
Общая схема математической модели (ММ) функционирования системы может быть представлена в виде:
Множество переменных ![]() вместе с законами функционирования
вместе с законами функционирования
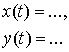
называется математической моделью системы.
Если t непрерывно, то модель называется непрерывной, иначе – дискретной:
.
Если модель не содержит случайных элементов, то она называется детерминированной, в противном случае – вероятностной, стохастической.
Если математическое описание модели слишком сложное и частично или полностью неопределенно, то в этом случае используются агрегативные модели.
Сущность агрегативной модели заключается в разбиении системы на конечное число взаимосвязанных частей (подсистем), каждая из которых допускает стандартное математическое описание. Эти подсистемы называются агрегатами.
2.3. Имитация случайных величин и процессов
Базовый датчик
Моделирование случайных элементов в системах является одной из самых базовых задач математического моделирования.
Любая случайная величина или процесс X может моделироваться следующим образом:

Базовый датчик выдает независимые равномерно распределенные случайные величины:
· непрерывные в (0,1);
· дискретные в ![]() .
.
Типы базовых датчиков:
· физические (любой физический шум), в последнее время практически не используются, т. к. характеристики нестабильны и реализацию повторить нельзя;
· псевдослучайные датчики строятся на основе детерминированного алгоритма, но полученные результаты мало отличны от случайных.
Псевдослучайные базовые датчики строятся по модели ![]()
![]()
при заданном x0.
Рассмотрим формулу получения случайных чисел
Хn+1 = (a Хn + c) mod m, n ³ 0 ,
характерную для линейной конгруэнтной последовательности случайных чисел, где
m — модуль, m > 0;
a — множитель, 0 £ a < m;
c — приращение, 0 £ с < m;
Х0 — начальное значение, 0 £ Х0 < m.
Пусть m = 16; Х0 =9; a = c = 5, тогда воспользовавшись последней формулой, получим последовательность
9, 2, 15, 0, 5, 14, 11, 12, 1,10,7,8,13,6,3,4,9…
Требования к базовым датчикам:
1. Отрезок апериодичности.
2. Равномерность.
3. Некоррелированность.
2.4. Основы математического моделирования
Отметим основные операции математического моделирования:
1. Линеаризация. Пусть дана математическая модель
М=М(X, Y, A),
где X - множество входов, Y - множество выходов, А - множество состояний системы. Схематически можно это изобразить так:
X![]() A
A![]() Y.
Y.
Если X, Y, A - линейные пространства (множества), а ![]() и
и ![]()
![]() : X
: X ![]() A,
A, ![]() : A
: A ![]() Y
Y
- линейные операторы, которые любые линейные комбинации ax + by преобразуют в линейные комбинации типа
A*![]() (x) + b*
(x) + b*![]() (y),
(y),
то система (модель) называется линейной. Все другие системы (модели) - нелинейные. Они труднее поддаются исследованию, хотя и более актуальны. Нелинейные модели менее изучены, поэтому их часто линеаризуют - сводят к линейным моделям.
Например, применим операцию линеаризации по Тейлору в точке t0 = 2 к процессу:
У(t) = bt2/2, 0 ![]() t
t ![]() 4,
4,
функция является нелинейной (квадратичной). Процедура линеаризации даст линейную модель вида y = -2b+2bt. Чтобы понять ответ, вспомним положение о разложении аналитической функции в ряд Тейлора.
Пусть f(t) - действительная непрерывная функция, имеющая в интервале с <= t < b n – ю производную. Тогда
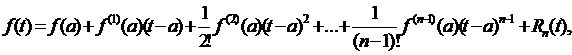
где Rn(t) – остаточный член разложения, а 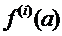 - производные i - го порядка функции f(t) в точке разложения
- производные i - го порядка функции f(t) в точке разложения ![]() . Ответ получен в точке
. Ответ получен в точке ![]() =2.
=2.
2. Идентификация. Пусть модель системы в общем виде представлена следующим образом:
М = М(X, Y, A), A = {ai}, ai = (ai1, ai2, ..., aik)
ai - вектор состояния объекта (системы). Если вектор ai зависит от некоторых неизвестных параметров, то задача идентификации состоит в определении модели или ее параметров по некоторым дополнительным условиям, например, экспериментальным данным, характеризующим состояние системы.
Идентификация – это задача построения по результатам наблюдений математических моделей, адекватно описывающих поведение системы.
Пусть S={s1, s2, ..., sn} - некоторая последовательность сообщений или данных, получаемых от источника информации о системе,
М={m1, m2, ..., mz} - последовательность моделей, описывающих систему S, среди которых, возможно, содержится оптимальная (в каком-то смысле) модель, то идентификация модели М означает, что последовательность S позволяет различать две разные модели в М.
Цель идентификации - построение надежной, адекватной, эффективно функционирующей, гибкой модели на основе минимального объема информативной последовательности сообщений.
Наиболее часто используемыми на практике методами идентификации систем являются:
· метод наименьших квадратов,
· метод максимального правдоподобия,
· метод байесовских оценок,
· метод марковских цепных оценок,
· метод эвристик,
· экспертное оценивание и др.
Пример. Применим операцию идентификации параметра b в модели у=bt2/2, 0 ![]() t
t ![]() 4.
4.
Решение. Зададим дополнительно значение y для некоторого t, например, y = 6 при t = 3. Тогда из у=bt2/2 получаем: 6 = 9b/2, b = 12/9 = 4/3. Идентифицированный параметр b определяет следующую модель y = 2t2/3. Методы идентификации моделей могут быть несоизмеримо сложнее, чем приведенный пример.
Оценка адекватности (точности) модели
Пример. Оценим адекватность (точность) модели, полученной в результате линеаризации. В качестве меры (критерия) адекватности рассмотрим привычную меру - абсолютное значение разности между точным значением и значением, полученным по модели. Если эта величина не велика и приемлема, то делается вывод о точности и адекватности модели, в противном случае – о малой точности модели и о нецелесообразности использования такой модели.
Для примера, рассмотренного выше, оценим точность модели. Для этого построим таблицу:
0 | Объект у=bt2/2 | Модель у’ = -2b+2bt | Точность модели | y - y’| |
0 | 0 | -2b | 2b |
1 | b/2 | -2b+2b=0 | b/2 |
2 | 2b | -2b+4b=2b | 0 |
3 | 9/2b=4.5b | -2b+6b=4b | 0.5 |
4 | 8b | -2b+8b=6b | 2b |
Среднее значение: | 0.9 b + 0.1 |
Анализ показывает, что точность моделирования зависит от значения b. Чем меньше b, тем точнее результат моделирования и наоборот.
Вычислительный эксперимент по модели - это эксперимент, осуществляемый с помощью моделирования на ЭВМ с целью определения состояния системы или прогноза реакции системы на различные входные сигналы. Орудием эксперимента здесь является компьютер и модель.
Отметим основные причины, тормозящие использование математического моделирования в новых условиях:
· традиционное описание модели системами математических уравнений, соотношений плохо структурированных и плохо формализуемых систем описываются с помощью экспертных данных, эвристических и имитационных процедур, интегрированных пакетов программ, графических образов и т. д.;
· существующие средства описания и представление моделей на ЭВМ не учитывают специфику моделирования, нет единого представления моделей, генерации новых моделей по банку моделей;
· недооценка возможностей компьютера, который может делать больше, чем простая реализация алгоритма, отсутствие доступа к опыту моделирования на ЭВМ.
При компьютерном моделировании главную роль играет алгоритм (программа), компьютер и технология, т. е. инструментальная система.
При имитационном моделировании главную роль играют технология и средства моделирования.
При работе с моделями нужно помнить. Модель не эквивалентна программе, а моделирование не сводится к программированию.
Основные функции ЭВМ при моделировании систем:
· исполнение роли вспомогательного средства для решения задач;
· исполнение роли средства постановки и решения новых задач;
· исполнение роли средства конструирования обучающих и моделирующих сред;
· исполнение роли средства моделирования для получения новых знаний;
· исполнение роли "обучения" новых моделей (самообучение модели).
Компьютерное моделирование есть основа представления знаний в ЭВМ, оно предполагает построение различных баз знаний.
Прогресс моделирования связан с разработкой систем компьютерного моделирования, которые поддерживает весь жизненный цикл модели. Автономные модели обмениваются информацией друг с другом через единую информационную шину - банк моделей, через базу знаний по компьютерному моделированию.
Особенность компьютерных систем моделирования - их высокая интеграция и интерактивность. Часто эти компьютерные среды функционируют в режиме реального времени.
Вычислительный эксперимент можно рассматривать как разновидность компьютерного моделирования.
Можно говорить сейчас и о специальных пакетах прикладных программ, текстовых, графических и табличных процессоров, о визуальных средах, особенно работающих в режиме реального времени, позволяющих осуществлять компьютерное моделирование.
Компьютерное моделирование и вычислительный эксперимент становятся новым инструментом, методом научного познания, новой технологией из-за возрастающей необходимости перехода от исследования линейных математических моделей систем к исследованию сложных и нелинейных математических моделей систем.
Грубо говоря, наши знания об окружающем мире - линейны и детерминированы, а процессы в окружающем мире нелинейны и стохастичны.
2.5. Компьютерное моделирование
Компьютерное моделирование от постановки задачи до получения результатов проходит следующие этапы:
1. Постановка задачи:
· формулировка задачи;
· определение цели и приоритетов моделирования;
· сбор информации о системе, объекте моделирования;
· описание данных (их структуры, диапазона, источника и т. д.).
2. Предмодельный анализ:
· анализ существующих аналогов и подсистем;
· анализ технических средств моделирования:
· ЭВМ;
· периферии.
· Анализ программного обеспечения:
· языков программирования;
· пакетов прикладных программ;
· инструментальных сред.
· Анализ математического обеспечения:
· моделей;
· методов;
· алгоритмов.
3. Анализ задачи (модели):
· разработка структур данных;
· разработка входных и выходных спецификаций, форм представления
данных;
· проектирование структуры и состава модели (подмоделей).
4. Исследование модели:
· выбор методов исследования подмоделей;
· выбор, адаптация или разработка алгоритмов;
· сборка модели в целом из подмоделей;
· идентификация модели при необходимости;
· формулировка используемых критериев адекватности, устойчивости и
чувствительности модели.
5. Программирование (проектирование программы):
· выбор метода тестирования и тестов (контрольных примеров);
· кодирование на языке программирования (написание команд);
· комментирование программы.
6. Тестирование и отладка:
· синтаксическая отладка;
· семантическая отладка (отладка логической структуры);
· тестовые расчеты, анализ результатов тестирования;
· оптимизация программы;
7. Оценка моделирования:
· оценка средств моделирования;
· оценка адекватности моделирования;
· оценка чувствительности модели;
· оценка устойчивости модели;
· документирование;
· описание задачи, целей;
· описание модели, метода, алгоритма;
· описание среды реализации;
· описание возможностей и ограничений;
· описание входных и выходных форматов, спецификаций;
· описание тестирования;
· создание инструкций для пользователя.
8. Сопровождение:
· анализ применения, периодичности использования, количества
пользователей, типа использования (диалоговый, автономный и др.),
анализ отказов во время использования модели;
· обслуживание модели, алгоритма, программы и их эксплуатация;
· расширение возможностей: включение новых функций или изменение
режимов моделирования, в том числе и под модифицированную среду;
· нахождение, исправление скрытых ошибок в программе.
9. Использование модели.
Математическое и компьютерное моделирование поэтапно рассмотрим на примере модели производства.
Этап 1. Содержательная постановка задачи
Современное производство характерно тем, что часть производимой продукции (в стоимостном выражении) возвращается в виде инвестиций (т. е. части конечной продукции, используемой для создания основных фондов производства) в производство. При этом время возврата, ввода в оборот новых фондов может быть различным для различного рода производства. Необходимо промоделировать эту ситуацию и выявить динамику изменения величины основных фондов производства (капитала).
Сложность и многообразие, слабая структурированность и плохая формализуемость основных экономических механизмов, определяющих работу предприятий, не позволяют преобразовать процедуры принятия решений в полностью эффективные математические модели и алгоритмы прогнозирования. Поэтому целесообразно использовать простые, гибкие и надежные процедуры принятия решения.
Рассмотрим одну такую простую модель социально-экономического процесса.
Этап 2. Формулировка гипотез, построение, исследование модели
Динамика изменения величины капитала определяется в модели простыми процессами производства и описывается обобщенными коэффициентами амортизации (расхода фондов) и потока инвестиций (часть конечного продукта, используемого в единицу времени для создания основных фондов). Эти коэффициенты - относительные величины (оцениваются за единицу времени).
Необходимо разработать и исследовать модель динамики основных фондов. Считаем при этом допустимость определенных гипотез, определяющих систему производства.
Пусть x(t) - величина основных фондов (капитала) в момент времени t, где 0 ![]() t
t ![]() N. Через промежуток времени Δt она будет равна x(t + Δt). Абсолютный прирост равен Δx = x(t + Δt) - x(t). Относительный прирост будет равен
N. Через промежуток времени Δt она будет равна x(t + Δt). Абсолютный прирост равен Δx = x(t + Δt) - x(t). Относительный прирост будет равен ![]() x = [x(t + Δt) - x(t)] / Δt.
x = [x(t + Δt) - x(t)] / Δt.
Примем следующие гипотезы:
1. Cоциально - экономические условия производства достаточно хорошие и способствуют росту производства, а поток инвестиций задается в виде известной функции y(t).
2. Коэффициент амортизации фондов считается неизменным и равным m, и при достаточно малом значении Δt, изменение основных фондов прямо пропорционально текущей величине капитала, тогда прибыль работы предприятия выразится:
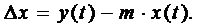
Считая Δt![]() 0 и учитывая определение производной, получим из предыдущего соотношения математическое выражение закона изменения величины капитала, т. е. математическую модель (дифференциальное уравнение) динамики капитала:
0 и учитывая определение производной, получим из предыдущего соотношения математическое выражение закона изменения величины капитала, т. е. математическую модель (дифференциальное уравнение) динамики капитала:
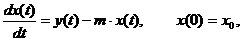
где х(0) - начальное значение капитала в момент времени t = 0.
Эта простейшая модель не отражает важного факта: социально-экономические ресурсы производства таковы, что между выделением инвестиций и их введением и использованием в выпуске новой продукции проходит время Т (лаг). Учитывая это, необходимо переписать модель в виде
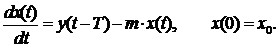
Этой непрерывной, дифференциальной, динамической модели можно поставить в соответствие простую дискретную модель:
хi+1 = хi + yj – m*хi, x0 = с, i = 0, 1, 2, …, n, j = 0, T, 2T,…<n.
где n - предельное значение момента времени при моделировании.
Дискретная модель следует из непрерывной при Δt = 1 при замене производной на относительное приращение, что справедливо при малых значениях Δt.
Этап 3. Построение алгоритма и программы моделирования
Возьмем для простоты режим моделирования, когда m, c - известны и постоянны, y - увеличивается в каждый следующий момент времени на 1%. Рассмотрим наиболее простой алгоритм моделирования в укрупненных шагах.
1. Ввод входных данных для моделирования: с = х(0) - начальный капитал; n - конечное время моделирования; m - коэффициент амортизации; s - единица измерения времени; y - инвестиции.
2. Вычисление xi от i = 1 до i = n по рекуррентной формуле, приведенной выше.
3. Поиск стационарного состояния, т. е. такого момента времени j, 0 ![]() j
j ![]() n, начиная с которого все хj, хj +1, …, хn постоянны или изменяются на малую допустимую величину ε >0.
n, начиная с которого все хj, хj +1, …, хn постоянны или изменяются на малую допустимую величину ε >0.
4. Выдача результатов моделирования и, по желанию пользователя, графика.
Этап 4. Проведение вычислительных экспериментов
Эксперимент 1. Поток инвестиций - постоянный и в каждый момент времени равенВ начальный момент капитал – 1 руб. Коэффициент амортизации - 0,0025. Найти величину основных фондов через 3 суток, если лаг равен 5 суток.
Решение. Воспользуемся формулой
хi+1 = хi + yj – m*хi, x0 = с, i = 0, 1, 2,3; j =0.
Здесь х0= с = 1 руб.; m = 0.0025; y0 = 10 000 руб.
yj выделяется раз в 5 суток.
Проведем расчет:
х1 = х0 + y0 – m*х0 = 1 000 000 + 10 000 – 0.0025* 1 000 000 = 1 007 500 (руб.);
х2 = х1 – m*х1 = 1 007 500 – 0.0025* 1 007 500 =
1 004 981.25 (руб.);
х3 = х2 – m*х2 = 1 004 981.25 – 0.0025* 1 004 981.25 = 1 002 468.7968 (руб.).
Эксперимент 2. Основные фонды в момент времени t = 0 были равны 5 000. Через какое время общая их сумма превысит руб., если поток инвестиций постоянный равный 2000 руб., известно, что m = 0.02, T=3 ?
Эксперимент 3. Какую стратегию инвестиций лучше использовать, если величина инвестиций постоянная, в начальный момент капитал равен 100 000 и величина амортизации постоянная?
Этап 5. Модификация (развитие) модели
Модификация 1. Коэффициент амортизации можно взять в форме m = r – s*x(t), где r - коэффициент обновления фондов, s - коэффициент устаревания фондов, причем 0 ![]() r, s
r, s ![]() 1. При этом модель примет вид
1. При этом модель примет вид
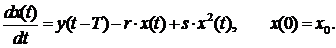
Этой непрерывной, дифференциальной, динамической модели можно поставить в соответствие простую дискретную модель:
хi+1 = хi + yj – r*хi + s*xi 2 ,
x0 = с, i = 0, 1, 2, …, n, 0 < j < n,
где n - предельное значение момента времени при моделировании.
Модификация 2. Одна из моделей математической экономики задается уравнением: dz / dt = ((1-c) * z(t) + k( t - w) - a) *l, где z(t) - функция, характеризующая выпуск продукции, k - коэффициент капиталовложений, a - независимые расходы производства, l - скорость реакции выпуска на капиталовложения, c - постоянная спроса, w - запаздывание (лаг).
3. Эволюционное моделирование и генетические алгоритмы
3.1. Основные атрибуты эволюционного моделирования
Потребность в прогнозе и адекватной оценке последствий, осуществляемых человеком мероприятий (особенно негативных), приводит к необходимости моделирования динамики изменения основных параметров системы, динамики взаимодействия открытой системы с ее окружением (ресурсы, потенциал, условия, технологии и т. д.), с которым осуществляется обмен ресурсами в условиях враждебных, конкурентных, кооперативных или же безразличных взаимоотношений.
Здесь необходимы системный подход, эффективные методы и критерии оценки адекватности моделей, направленные не только на максимизацию критериев типа: "прибыль", "рентабельность", но и на оптимизацию отношений с окружающей средой.
Для долгосрочного прогноза необходимо выделить и изучить достаточно полную и информативную систему параметров исследуемой системы и ее окружения, разработать методику введения мер информативности и близости состояний системы. Важно отметить, что при этом некоторые критерии и меры могут часто конфликтовать друг с другом.
Многие такие социально-экономические системы можно описывать с единых позиций, средствами и методами единой теории - эволюционной.
При эволюционном моделировании процесс моделирования сложной социально - экономической системы сводится к созданию модели его эволюции или к поиску допустимых состояний системы, к процедуре (алгоритму) отслеживания множества допустимых состояний (траекторий).
При исследовании эволюции системы необходима ее декомпозиция на подсистемы с целью обеспечения:
· эффективного взаимодействия с окружением;
· оптимального обмена ресурсами ( материальными, энергетическими, информационными, организационными ) с подсистемами;
· эволюции системы в условиях динамической смены и переупорядочивания целей, структурной активности и сложности системы;
· управляемости системы, идентификации управляющей подсистемы и эффективных связей с подсистемами, обратной связи.
Пусть имеется некоторая система S с N подсистемами. Для каждой i - й подсистемы определим вектор x(i) = (x1(i), x2(i),…,xni(i)) основных параметров, без которых нельзя описать и изучить функционирование подсистемы в соответствии с целями и доступными ресурсами системы. Введем в рассмотрение функцию s(i) = s(x(i)), которую назовем функцией активности или просто активностью подсистемы. Например, в бизнес-процессах это понятие близко к понятию деловой активности.
Для всей системы определены вектор состояния системы x и активность системы s(x), а также понятие общего потенциала системы.
Например, потенциал активности может быть определен с помощью интеграла от активности на задаваемом временном промежутке моделирования.
Эти функции отражают интенсивность процессов, как в подсистемах, так и в системе в целом.
Важными для задач моделирования являются три значения
s(i)max, s(i)min, s(i)opt
- максимальные, минимальные и оптимальные значения активности i - й подсистемы, а также аналогичные значения для всей системы (smax, smin, sopt).
Если дана открытая экономическая система (процесс), а Н0, Н1 - энтропия системы в начальном и конечном состояниях процесса, то мера информации определяется как разность вида:
ΔН = Н0 - Н1.
Энтропия – мера отклонения реального процесса от идеального.
Энтропия в теории управления – мера неопределенности состояния или поведения системы в данных условиях.
Энтропия динамической системы – мера хаотичности в поведении траекторий системы.
Уменьшение ΔН свидетельствует о приближении системы к состоянию статического равновесия (при доступных ресурсах), а увеличение - об удалении. Величина ΔН - количество информации, необходимой для перехода от одного уровня организации системы к другой (при ΔН > 0 - более высокой, при ΔН < 0 - более низкой организации).

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 |





