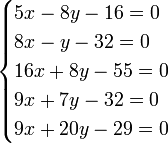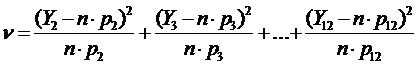 (4.6)
(4.6)
Эта статистика называется статистикой «хи - квадрат» наблюдаемых значений Y2 … Y12 при бросании игральных костей. Используя табл. 4.1, получим :
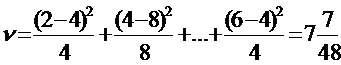 .
.
Формулу (4.6) перепишем следующим образом:
| (4.7) |
Так как
![]() ,
,
Y1 + Y2 +…+ Yk = n,
p1 + p2 +…+ pk =1.
Чтобы воспользоваться c2 - статистикой проводят несколько экспериментов, затем вычисляют числа ![]() . Далее используют известные таблицы c2-распределения имеющие вид [4]:
. Далее используют известные таблицы c2-распределения имеющие вид [4]:
Таблица 4.2
p = 99% | p = 95% | p = 75% | p = 50% | p = 25% | p = 5% | p = 1% | |
… | |||||||
| 2,558 | 3,940 | 6,737 | 9,342 | 12,55 | 18,31 | 23,21 |
… |
Здесь p — процентные точки c2 - распределения; m = k – 1 — число степеней свободы, что на единицу меньше, чем число категорий. Внутри клеток таблицы стоят числа ![]() .
.
Предположим, что были сделаны три эксперимента с генерированием случайных последовательностей и получены числа:
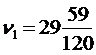 ,
, 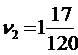 ,
, 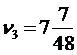 .
.
Сравнивая эти величины со значениями таблицы 4.2 при 10 степенях свободы, мы видим, что ![]() 1 гораздо больше, чем 23.21, а это может произойти только в 1% случаев. В связи с этим эксперимент 1 демонстрирует значительное отклонение от случайного поведения.
1 гораздо больше, чем 23.21, а это может произойти только в 1% случаев. В связи с этим эксперимент 1 демонстрирует значительное отклонение от случайного поведения. ![]() 2 показывает не лучшие свойства, так как результаты слишком близки к ожидаемым. Наконец, значение
2 показывает не лучшие свойства, так как результаты слишком близки к ожидаемым. Наконец, значение ![]() 3 находится между 75 и 50 - процентной точками. Таким образом, наблюдение является удовлетворительно случайным по отношению к этому критерию.
3 находится между 75 и 50 - процентной точками. Таким образом, наблюдение является удовлетворительно случайным по отношению к этому критерию.
Отметим, таблица 4.2 — это только приближенные значения c2 распределения, которое является предельным распределением случайной величины ![]() формулы (4.7). Поэтому табличные значения близки к реальным только при больших n.
формулы (4.7). Поэтому табличные значения близки к реальным только при больших n.
Насколько большими должны быть n? Эмпирическое правило гласит: нужно взять n настолько большим, чтобы все значения n pS были больше или равны пяти.
4.3. Эмпирические критерии
Эмпирические критерии традиционно применяются для проверки, будет ли последовательность случайной. Обычно каждый такой критерий применяется к последовательности
{Un} = U0, U1, U2, … (4.8)
действительных чисел, которые предполагаются независимыми и равномерно распределенными в интервале (0,1).
Если критерии используются для целочисленных последовательностей, то используется вспомогательная последовательность
{Yn} = Y0, Y1, Y2, …, (4.9)
определенная правилом
Yn = [d × Un ] (4.10)
Это последовательность целых чисел, распределенных в интервале (0, d–1). Число d выбирается таким образом, чтобы сделать все Yi — целыми. Обычно d выбирается достаточно большим, но не настолько большим, чтобы критерий стал практически неприменим.
Критерий равномерности (критерий частот)
Первое требование, предъявляемое к последовательности (4.8) состоит в том, чтобы ее члены были числа, равномерно распределенные между 0 и 1. Существуют 2 способа проверить это:
1. Использовать критерий Колмогорова-Смирнова [2] .
2. Использовать c2-критерий.
Для того чтобы применить c2-критерий, используется последовательность (4.10) вместо (4.8). Для каждого r, 0 £ r < d, подсчитывается число случаев, когда Yj = r. Затем применим c2 – критерий, принимая число категорий k = d, а вероятности pS = 1/d для каждой категории. d — число, равное, например, 64 или 128 .
Критерий серий
Более общее требование к последовательности состоит в том, чтобы пары последовательных чисел были равномерно распределены независимым образом.
В критерии серий подсчитывается число случаев, когда пара (Y2j, Y2j+1) = (q, r) для 0 £ j < n. Такая операция осуществляется для каждой пары целых чисел q и r, таких, что 0 £ q< r < d. Затем применяется c2 - критерий к этим k = d2 категориям, где 1/d2 — вероятность отнесения пары чисел к каждой из категорий. При этом d выбирается таким образом, чтобы n>>k, например n ³ 5d2.
Покер-критерий (критерий разбиений)
«Классический» покер-критерий рассматривает n групп по пять последовательных целых чисел
{Y5j, Y5j+1, Y5j+2, Y5j+3, Y5j+4} для 0 £ j < n
и проверяет, какие из следующих семи комбинаций соответствуют таким пятеркам чисел (порядок не имеет значения):
Все числа разные: a b c d e
Одна пара: a a b c d
Две пары: a a b b c
Три числа одного вида: a a a b c
Полный набор: a a a b b
Четыре числа одного вида: a a a a b
Пять чисел одного вида: a a a a a
c2 - критерий основан на подсчете числа комбинаций пятерок в каждой из семи категорий имеющих место в n – группах, состоящих из 5 элементов.
В [3] можно ознакомиться с другими известными критериями, которые традиционно применяются для проверки, будет ли последовательность случайной.
Возникает вопрос: «Зачем применять такое количество критериев?» Необходимость проверки последовательности с помощью нескольких критериев позволяет сделать вывод о случайности генерируемых чисел, а значит и точности моделирования процессов с их использованием.
4.4. Генерация случайных чисел с заданным распределением
При использовании случайных чисел часто требуются помимо равномерного распределения и другие виды распределений в зависимости от приложений. Например, необходимо моделировать случайное время ожидания между появлениями независимых событий, что достигается на основе применения показательного распределения случайных чисел. Иногда в случайных числах нет необходимости, но нужны случайные перестановки (случайное размещение n объектов) или случайное сочетание (случайный выбор k объектов из совокупности, содержащей n объектов).
В принципе любая из этих случайных величин может быть получена из равномерно распределенных случайных величин U0 , U1 , …, где Ui Î [0, 1].
Случайный выбор из ограниченного множества
В общем случае случайные целые числа X, которые лежат между 0 и k–1, можно получить, умножив U на k и положив X = ëk × Uû (ближайшее целое снизу).
В общем случае можно получить, если необходимо, различные веса для целых чисел. Рассмотрим такую процедуру. Предположим, что значение X = x1 должно быть получено с вероятностью p1, X = x2 — с вероятностью p2, … и X = xk — с вероятностью pk.
Для получения такой последовательности чисел сначала генерируется равномерное случайное число U Î [0, 1] и полагается
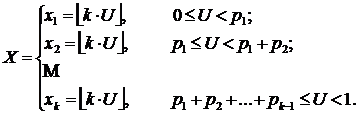
Здесь все pk считаются заданными и ![]() .
.
Общие методы для непрерывных распределений
В общем случае распределение действительных чисел может быть выражено в терминах «функции распределения» F(X), которая точно определяет вероятность того, что случайная величина X не превысит значения x:
F(X) = Pr (X £ x) (4.11)
Эта функция всегда монотонно возрастает от 0 до 1 и
F(x1) £ F(x2), если x1 £ x2;
F(-¥) = 0, F(+¥) = 1.
Если F(X) непрерывна и строго возрастающая, такая что
F(x1) < F(x2) , когда x1 < x2, то она принимает все значения между 0 и 1 и для нее существует обратная функция F-1(y) такая, что для 0 < y < 1 Y = F(X), тогда и только тогда, когда
X = F -1(y).
В большинстве случаев, когда F(X) непрерывна и строго возрастает, можно вычислить случайную величину X с распределением F(X), полагая
X = F -1 (U),
где U — равномерно распределенная случайная величина.
Заметим, что если х1 — случайная величина, имеющая функцию распределения F1(Х), и если х2 — независимая от х1 случайная величина с функцией распределения F2(Х),
то max (х1, х2) имеет распределение F1(Х) × F2(Х),
min (х1, х2) имеет распределение F1(Х) + F2(Х) – F1(Х) × F2(Х).
Любой алгоритм, использующий случайные числа на входе, дает на выходе случайные величины с некоторым распределением.
Нормальное распределение
Возможно, наиболее значительным неравномерным распределением является нормальное распределение с нулевым средним значением и среднеквадратичным отклонением, равным единице:
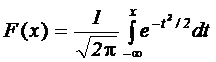 (4.12)
(4.12)
Рассмотрим алгоритм вычисления двух независимых нормально распределенных случайных величин: X1 и X2.
(Метод полярных координат)
Р1. [Получение равномерно распределенных случайных величин.] Сгенерировать две независимые случайные величины U1 и U2, равномерно распределенные между 0 и 1. Присвоить V1 2U1 – 1, V2 2U2 – 1. (Здесь V1 и V2 равномерно распределены между –1 и +1.)
Р2. [Вычисление S.] Присвоить S V12 + V22.
Р3. [Проверить S ³ 1?] Если S ³ 1 возврат к п. Р1.
Р4. [Вычисление X1, X2.] Присвоить X1 и X2 следующие значения:
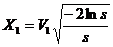 ,
, ![]() .
.
Х1 и Х2 - сгенерированные нормально распределенные случайные величины.
Показательное распределение
После равномерного и нормального распределений следующим важным распределением случайной величины является показательное распределение. Такое распределение появляется в ситуации «время поступления». Например, если одна заявка в среднем поступает каждые m секунд, то время между двумя последовательными поступлениями имеет показательное распределение со средним, равным m. Это распределение задается формулой
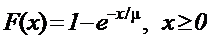 . (4.13)
. (4.13)
Метод логарифма. Очевидно, если
![]() , то
, то
![]() .
.
В [5] предлагается 1 – y рассматривать как равномерное распределение 1 – U, или просто U, что позволяет записать:
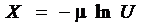 ,
,
где X — случайная величина, имеющая экспоненциальное распределение со средним, равным m.
4.5. Признаки случайной последовательности
Приведем утверждение : «Последовательность
{Un} = U0, U1, U2, …
случайна, если она обладает любыми свойствами, присущими всем бесчисленным последовательностям независимых выборок случайных равномерно распределенных величин».
Отметим важные определения и замечания, необходимые в понимании, что такое случайная последовательность. Последовательность {Un} = U0, U1, U2, … равно распределена тогда и только тогда, когда
Pr(U £ Un < v) = v – U
для всех действительных чисел U, v при 0 £ U < v < 1. Вспомним, что последовательность может быть равно распределена, даже если она не случайна.
Процедура получения простейшего генератора случайных чисел
В начале целой переменной X присваивается некоторое значение X0. Эта величина X используется только для начала генерирования случайных чисел по формуле:
X = (aX + c) mod m.
Теперь полученное новое значение X может использоваться качестве случайной величины. При этом необходимо тщательно выбирать X0, a, c, m и разумно использовать случайные числа согласно следующим принципам:
1. Начальное число X0 выбирается произвольно. Если программа используется несколько раз, и каждый раз требуются различные источники случайных чисел, то нужно присвоить X0 последнее значение X на предыдущем прогоне или присвоить X0, если это удобно, текущую дату и время.
2. Число m должно быть большим, но меньше, чем 230. Удобно его брать равным размеру компьютерного слова. Вычисление (aX + c) mod m должно быть точным без округления ошибки.
3. Если m — степень 2, выбираем a таким, чтобы a mod 8 = 5. Одновременный выбор a и c даст гарантию, что генератор случайных чисел будет вырабатывать все m различных возможных значений X прежде, чем они начнут повторяться.
4. Множитель a предпочтительнее выбирать между .01* m и .099* m.
5. Значение c не существенно, когда a — хороший множитель, за исключением того, что c не должно иметь общего множителя с m, когда m — размер компьютерного слова. Таким образом, можно выбирать c = 1 или c = a.
6. Младшие значащие цифры (справа) X не очень случайны, так что решения, основанные на числе X, всегда должны опираться, главным образом, на старшие значащие цифры. Обычно лучше считать X случайной дробью X/m между 0 и 1. Далее, чтобы подсчитать случайное целое число между 0 и k–1, нужно умножить его на k и округлить результат.
7. Желательно генерировать не более m/1000 чисел, иначе последующие будут вести себя подобно предыдущим.
Замечание. При работе с генераторами случайных чисел, необходимо по крайней мере дважды использовать совершенно разные источники случайных чисел, прежде чем получить решения. Это будет указывать на стабильность результатов, а также оградит от опасного доверия к генераторам со скрытыми недостатками.
5. Статистическое моделирование
5.1. Введение
Статистическое моделирование – исследование объектов, систем на их статистических моделях; построение и изучение моделей с целью получения объяснения явлениям, происходящим в объектах, системах, а также для предсказания явлений или показателей, интересующих исследователя.
Оценка параметров таких моделей производится с помощью статистических методов:
· метода максимального правдоподобия;
· метода наименьших квадратов;
· метода моментов.
Метод максимального правдоподобия - метод оценивания неизвестного параметра путем максимизации функции правдоподобия. Он основан на предположении о том, что вся информация о статистической выборке содержится в функции правдоподобия.
Метод максимального правдоподобия соответствует многим известным методам оценки в области статистики. Например, предположим, что вы заинтересованы ростом жителей Поволжья. Предположим, у вас данные роста некоторого количества людей, а не всего населения. Кроме того предполагается, что рост является нормально распределенной величиной с неизвестной дисперсией и средним значением. Среднее значение и дисперсия показателя роста для такой выборки является максимально правдоподобным к среднему значению и дисперсии всего населения Поволжья.
Для фиксированного набора данных и базовой вероятной модели, используя метод максимального правдоподобия, мы получим значения параметров модели, которые делают данные «более близкими» к реальным. Оценка максимального правдоподобия дает уникальный и простой способ решения в случае нормального распределения.
Метод применяется в широких областях науки, в том числе:
· в системах связи;
· при моделировании в ядерной физике и физике элементарных частиц;
· при моделировании каналов в транспортных сетях и др.
5.2. Нормальное распределение
Нормальное распределение, также называемое гауссовским распределением, т. е. распределением вероятностей, которое играет важнейшую роль во многих областях знаний, особенно в физике. Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.
Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством. Значения этих параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).
Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.
Если случайные величины X1 и X2 независимы и имеют нормальное распределение с математическими ожиданиями μ1 и μ2 и дисперсиями ![]() и
и ![]() соответственно, то X1 + X2 также имеет нормальное распределение с математическим ожиданием μ1 + μ2 и дисперсией
соответственно, то X1 + X2 также имеет нормальное распределение с математическим ожиданием μ1 + μ2 и дисперсией 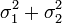 .
.
Простейшие, но неточные методы моделирования основываются на центральной предельной теореме. Именно, если сложить много независимых одинаково распределённых величин с конечной дисперсией, то сумма будет распределена примерно нормально. Например, если сложить 12 независимых базовых случайных величин, получится грубое приближение стандартного нормального распределения. Тем не менее, с увеличением слагаемых распределение суммы стремится к нормальному.
Нормальное распределение часто встречается в природе, нормально распределёнными являются следующие случайные величины:
- отклонение при стрельбе; ошибки при измерениях; рост человека и др.
Такое широкое распространение закона связано с тем, что он является предельным законом, к которому приближаются многие другие (например, биномиальный).
Доказано, что сумма очень большого числа случайных величин, влияние каждой из которых близко к 0, имеет распределение, близкое к нормальному. Этот факт является содержанием центральной предельной теоремы.
Центральная предельная теорема – теорема, утверждающая, что сумма большого количества слабозависимых случайных величин имеет распределение, близкое к нормальному.
Пусть ![]() есть бесконечная последовательность независимых одинаково распределённых случайных величин, имеющих конечные математическое ожидание и дисперсию. Обозначим последние через μ и σ2 соответственно. Пусть
есть бесконечная последовательность независимых одинаково распределённых случайных величин, имеющих конечные математическое ожидание и дисперсию. Обозначим последние через μ и σ2 соответственно. Пусть
![]()
тогда
![]()
при ![]() , где N(0,1) — нормальное распределение с нулевым математическим ожиданием и стандартным отклонением, равным единице. Обозначив символом
, где N(0,1) — нормальное распределение с нулевым математическим ожиданием и стандартным отклонением, равным единице. Обозначив символом ![]() выборочное среднее первых n величин, то есть
выборочное среднее первых n величин, то есть 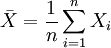 ,
,
далее мы можем переписать результат центральной предельной теоремы в следующем виде:
![]()
при ![]() .
.
5.3. Оценка максимального правдоподобия
Определение. Пусть имеем выборку ![]() из распределения
из распределения ![]() , где
, где ![]() — неизвестный параметр. Пусть
— неизвестный параметр. Пусть ![]() — функция правдоподобия, где
— функция правдоподобия, где 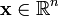 .
.
Точечная оценка
![]()
называется оценкой максимального правдоподобия параметра θ. Таким образом, оценка максимального правдоподобия — это такая оценка, которая максимизирует функцию правдоподобия при фиксированной реализации выборки.
5.4. Метод наименьших квадратов
Метод наименьших квадратов — один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки.
Метод наименьших квадратов применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.
Когда искомая величина может быть измерена непосредственно, как, например, длина отрезка или угол, то, для увеличения точности, измерение производится много раз, и за окончательный результат берут арифметическое среднее из всех отдельных измерений. Это правило арифметической середины основывается на соображениях теории вероятностей; легко показать, что сумма квадратов отклонений отдельных измерений от арифметической середины будет меньше, чем сумма квадратов отклонений отдельных измерений от какой бы то ни было другой величины. Само правило арифметической середины представляет простейший случай метода наименьших квадратов.
Решение уравнений по способу наименьших квадратов даёт возможность выводить вероятные ошибки неизвестных, то есть даёт величины, по которым судят о степени точности выводов.
Пусть надо решить систему уравнений
| (5.1) |
число которых более числа неизвестных x, y, ![]()
Чтобы решить их по способу наименьших квадратов, составляют новую систему уравнений, число которых равно числу неизвестных и которые затем решаются по обыкновенным правилам алгебры. Эти новые нормальные уравнения составляются по следующему правилу: умножают сначала все данные уравнения на коэффициенты при первой неизвестной x и, сложив их члены соответственно, получают первое нормальное уравнение. Затем умножают все данные уравнения на коэффициенты при второй неизвестной y и, сложив члены соответственно, получают второе нормальное уравнение и т. д. Введем для краткости выводов следующие обозначения:
|
тогда нормальные уравнения представятся в следующем простом виде:
| (5.2) |
Коэффициент при первой неизвестной во втором уравнении равен коэффициенту при второй неизвестной в первом, коэффициент при первой неизвестной в третьем уравнении равен коэффициенту при третьей неизвестной в первом и т. д. Для пояснения сказанного ниже приведено решение пяти уравнений с двумя неизвестными:
|
Составив значения [aa], [ab], получаем следующие нормальные уравнения:

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 |




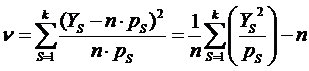 ,
,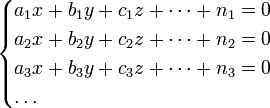
![\begin{cases}
{[}aa{]} = a_{1}a_{1} + a_{2}a_{2} + \dots \\
{[}ab{]} = a_{1}b_{1} + a_{2}b_{2} + \dots \\
{[}ac{]} = a_{1}c_{1} + a_{2}c_{2} + \dots \\
\dots\\
{[}ba{]} = b_{1}a_{1} + b_{2}a_{2} + \dots \\
{[}bb{]} = b_{1}b_{1} + b_{2}b_{2} + \dots \\
{[}bc{]} = b_{1}c_{1} + b_{2}c_{2} + \dots \\
\dots\\
\end{cases}](/text/78/388/images/image099_0.png)
![\begin{cases}
{[}aa{]}x + {[}ab{]}y + {[}ac{]}z + \dots + {[}an{]} = 0 \\
{[}ba{]}x + {[}bb{]}y + {[}bc{]}z + \dots + {[}bn{]} = 0 \\
{[}ca{]}x + {[}cb{]}y + {[}cc{]}z + \dots + {[}cn{]} = 0 \\
\dots\\
\end{cases}](/text/78/388/images/image100_0.png)