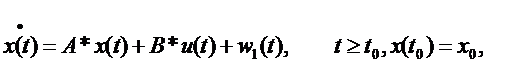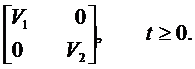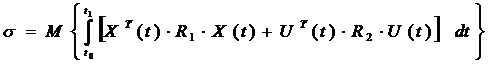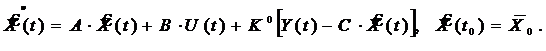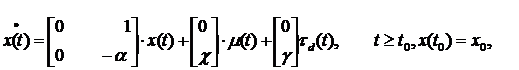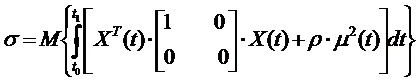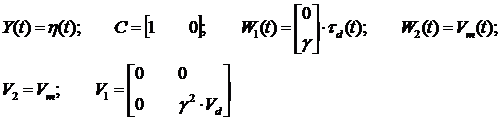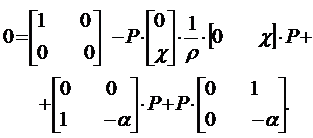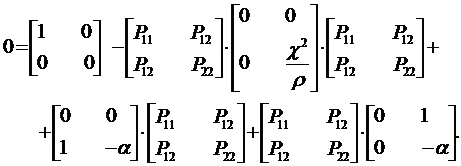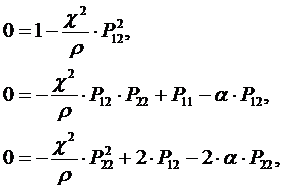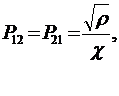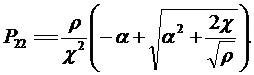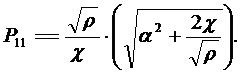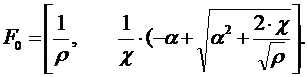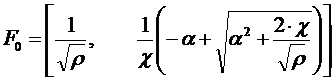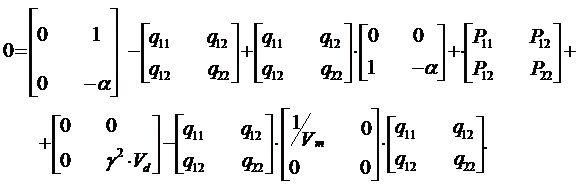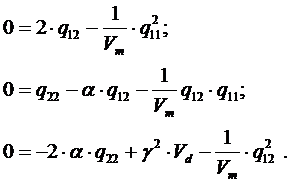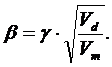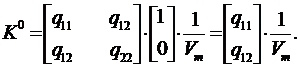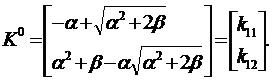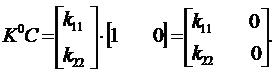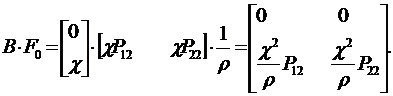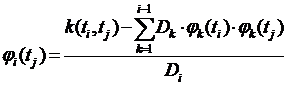
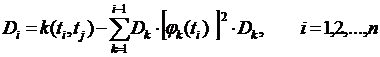
11.2. Имитация стационарных СП
Для стационарных СП справедливы соотношения:
![]()
Один из методов имитации стационарных СП заключается в вычислении F(ti) по формулам:
F(t1)=m+c1x1+c2x2+ . . . +cnxn,
F(t2)=m+c1x2+c2x3+ . . . +cnxn+1,
. .
F(tn)=m+c1xn+c2xn+1+ . . . +cnx2n-1.
Здесь хi - реализации некоррелированных случайных величин ![]() , для которых M[
, для которых M[![]() ] = 0,
] = 0, 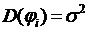 , закон их распределения задан. Коэффициенты cj, (j = 1,2,…,n ) вычисляются на основе решения уравнений:
, закон их распределения задан. Коэффициенты cj, (j = 1,2,…,n ) вычисляются на основе решения уравнений:
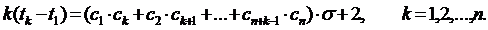
11.3. Имитация стационарных нормальных СП
Рассмотренные выше методы пригодны для моделирования СП, заданных на конечном интервале времени. При формировании реализаций большой длины эти методы трудоемки, что затрудняет их использование. На практике приходится моделировать СП, относящиеся к узкому классу СП: стационарных; стационарных и нормальных; нестационарных; СП со стационарными приращениями и т. д. Для таких классов СП существуют моделирующие алгоритмы. В их основу положены линейные преобразования стационарной последовательность F(tk) независимых нормальных случайных чисел (белый шум) в последовательность F(tk),( k = 1, 2, . . .),
( tk - tk-1= ![]() t = const), коррелированную по заданному закону. При этом оператор линейного преобразования записывается либо в виде формулы скользящего суммирования с некоторым весом аi:
t = const), коррелированную по заданному закону. При этом оператор линейного преобразования записывается либо в виде формулы скользящего суммирования с некоторым весом аi:
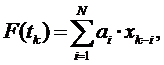
либо как рекуррентное соотношение вида:
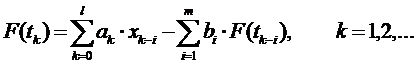
Коэффициенты аi и bi в обеих формулах и их количество зависит от вида корреляционной функции. Первая из приведенных формул является математической моделью (ММ) не рекурсивного цифрового фильтра, вторая - ММ рекурсивного цифрового фильтра.
12. Обработка результатов моделирования
В процессе имитационного моделирования формируется большое количество реализаций, являющихся исходным статистическим материалом для нахождения приближенных значений показателей эффективности, их оценок. В этих условиях обработка результатов моделирования может решаться только с применением методов, оптимальных по времени и обеспечивающих экономию памяти ЭВМ.
12.1. Оценка вероятности
Оценкой вероятности является частота
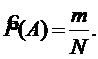
Для ее получения обычно организуют на программном уровне 2 счетчика: один для подсчета общего количества экспериментов N, второй - для подсчета общего количества положительных исходов m.
Иногда в качестве характеристик исследуемой системы выступает закон плотности распределения. Его приближенно можно охарактеризовать гистограммой. Для этого интервал изменения СВ разбивают на отрезки t i, каждому из них сопоставляют счетчик, где накапливают mi - количество попаданий значений СВ в ti. На каждом t i строится прямоугольник с высотой
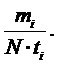
При необходимости полученную гистограмму можно сгладить.
12.2. Оценка математического ожидания и дисперсии
Оценку математического ожидания получают как среднее арифметическое значение СВ:
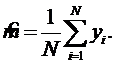
Сумму лучше всего вычислять (во избежание непроизводительных затрат памяти) путем постепенного накапливания.
Оценку дисперсии можно вычислять по формуле:
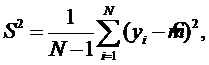
однако это связано с непроизводительным использованием памяти ЭВМ. Поэтому лучше воспользоваться формулой:
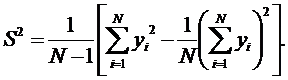
12.3. Оценка характеристик случайного процесса
Для оценки корреляционного момента двух случайных величин x, y рекомендуется использовать формулу:
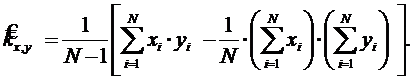
Для вычисления оценки характеристик СП производят статистическую обработку по N реализациям СП. Для этого интервал СП разбивают на части с 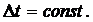 Мат. ожидания и дисперсии для каждого
Мат. ожидания и дисперсии для каждого 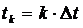 можно вычислить по формулам, приведенным выше. Оценку корреляционной функции можно вычислить по формуле:
можно вычислить по формулам, приведенным выше. Оценку корреляционной функции можно вычислить по формуле:
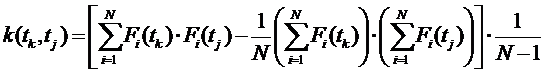
Здесь ![]() ,
, 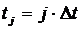 .
.
12.4. Количество реализаций, обеспечивающих заданную точность
Важной задачей обработки информации является задача определения количества реализаций N, обеспечивающих заданную точность получения оценок. Для определения N при оценке вероятности b пользуются формулой:
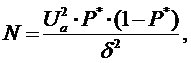
а при оценке мат. ожидания пользуются формулой:
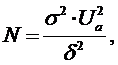
В формулах ![]() - квантиль, для нормального, центрированного нормального закона распределения, соответствующий значению
- квантиль, для нормального, центрированного нормального закона распределения, соответствующий значению ![]() где P заданная достоверность;
где P заданная достоверность; ![]() - оцениваемая вероятность;
- оцениваемая вероятность; ![]() - дисперсия;
- дисперсия; ![]() - допустимая погрешность. В этих формулах
- допустимая погрешность. В этих формулах ![]() неизвестно, а
неизвестно, а ![]() может быть неизвестным. Поэтому производят предварительно 50-100 реализаций, получают по ним оценки
может быть неизвестным. Поэтому производят предварительно 50-100 реализаций, получают по ним оценки ![]() и
и ![]() , подставляют их в формулы для вычисления уточненного значения N.
, подставляют их в формулы для вычисления уточненного значения N.
13. Стохастическое линейное оптимальное регулирование
13.1.Теоретические основы стохастического регулирования
Рассмотрим систему:
| (13.1) |
где x0 – стохастический вектор со средним значением
![]()
и матрицей дисперсий Q0 . Наблюдаемая переменная описывается выражением:
y (t) = Cx(t) + w2 (t), t ≥ t
Совместный случайный процесс w(t) = [w1 (t) w2 (t)]T является белым шу -
мом с интенсивностью:
| (13.3) |
Тогда задача стохастического линейного оптимального регулирования с обратной связью по выходной переменной является задачей нахождения такого функционала:
u (t) = f [y (τ), t 0 ≤ τ ≤ t ], t 0 ≤ t ≤ t1 , (13.4)
при котором критерий:
| (13.5) |
достигает минимума. Здесь R1, R2 – симметрические весовые матрицы, такие, что R1 > 0, R2 > 0, t0 ≤ t ≤ t1.
Запишем решение задачи стохастического линейного регулирования
с обратной связью по выходной переменной. Для входной переменной
имеем:
| (13.6) |
где
| (13.7) |
Здесь P – решение уравнения Риккати:
| (13.8) |
Оценка x(t) получается как решение уравнения:
| (13.9) |
где
| (13.10) |
Матрица дисперсий Q является решением уравнения Риккати:
| (13.11) |
13.2. Решение задач стохастического линейного оптимального регулирования
Задача 13.1. Система управления положением описывается диффе-
ренциальным уравнением вида:
| (13.12) |
где Х (t) = [Х1 (t) Х2 (t)]Т; τ d (t) – белый шум с постоянной скалярной интенсивностью Vd. Предположим, что наблюдаемая переменная определяет-
ся выражением:
| (13.13) |
где νm(t) – белый шум с постоянной скалярной интенсивностью Vm.
Критерий оптимальности имеет вид:
| (13.14) |
определить u(t), K0.
Решение. В обозначениях (13.1) – (13.11) имеем
| (13.15) |
Подставляя (13.15) в (13.8), получим:
| (13.16) |
Пусть Рij, (i, j = 1,2) обозначают элементы матрицы Р. Тогда, учитывая Р12 = Р21, получим из (13.16)
| (13.17) |
Сложим элементы матриц друг с другом, соблюдая порядок равенства индексов элементов матриц. Составим уравнения на основе приравнивания к нулю элементов матрицы, получим следующие алгебраические уравнения:
| (13.18) |
Из (13.18) определим Р11, Р12, Р22. Будем иметь
| (13.19) |
| (13.20) |
| (13.21) |
Определим матрицу F0 из соотношения (13.7). Получим:
| (13.22) |
Соотношение (13.22) с учетом (13.19), (13.20) примет вид:
| (13.23) |
Таким образом:
| (13.24) |
Используя (13.11), определим Q. Пусть qij, (i, j = 1,2) обозначают элементы
матрицы Q. Тогда, учитывая q12 = q21, получим из (13.11) следующее уравнение:
|
или
| (13.25) |
Из (13.25) получим следующие алгебраические уравнения:
| (13.26) |
Из (13.26) определим q11, q12, q22. Получим:
| (13.27) |
| (13.28) |
| (13.29) |
где
| (13.30) |
Определим матрицу K0 из (13.10). Будем иметь:
| (13.31) |
Соотношение (13.31) с учетом (13.27), (13.28) примет вид:
| (13.32) |
Из (13.9) имеем:
| (13.33) |
Определим матрицу D вида:
D = A – K0C – BF0. (13.34)
Будем иметь:
|
|
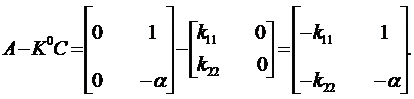
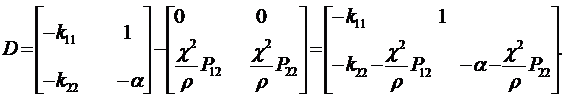
Примем следующие численные значения параметров:
χ = 0,787 рад /В ⋅ с 2 ,
α = 4,6 с −1 ,
ρ = 0,00002 рад 2/ В 2 ,
γ = 0,1 кг −1 ⋅ м −2 ,
Vd = 10 Н 2 ⋅ м 2 ⋅ с,
Vm = 10 −7 рад 2 /с.
Имеем:
k11 = 40,36; k 22 = 814,34; P12 = 0,00568; P22 = 0,00047.
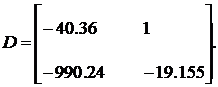
Характеристический полином матрицы D можно найти в виде

Характеристическое уравнение имеет вид:
S 2 + 59.5S + 1763.3 = 0 .
Найдем корни характеристического уравнения. Получим:
S1, 2 = −29,75 ± i59,27 .
Таким образом, система, описываемая уравнением (13.33) , устойчива.
Литература
1. , Федосин систем. Учебно-практическое
пособие. Интернет - Университет Информационных Технологий: БИНОМ.
Лаборатория знаний. 2010. – 231 с.
2. Казиев в анализ, синтез и моделирование систем.
htpp://www. *****, 2010.
3. , Постовалов статистика. Правила про-
верки согласия опытного распределения с теоретическим. – Новосибирск:
Изд-во НГТУ. – 1999. – 86 с.
4. Кнут Искусство программирования. Т. 2. Получисленные
алгоритмы: Уч. пос. - М.: Издательский дом «Вильямс», 2000.-832 с.
5. , Липатов указания к
практическим занятиям по курсу «Теоретические основы
автоматизированного управления». Пермь: Перм. гос. ун-т, 2006.
8. , , Носов теория
конструирования систем управления. Учебник для вузов. М.: Высшая
школа, 2003. С. 501-503.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 |