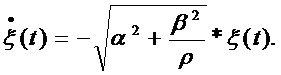
Система, поведение которой описывается таким уравнением, является асимптотически устойчивой, т. к. получена с учетом минимума функционала (9.2).
Рассмотрим другую методику решения задачи синтеза оптимального управления заданным объектом на основе моделирования процессов в комплексной области [6-7] и сравним оба подхода между собой.
Перепишем уравнения (9.6) , (9.11) в виде:
| (9.14) |
Применим к функциям преобразование Лапласа, будем иметь:
| (9.15) |
Из первого уравнения выразим X(s).Получим:
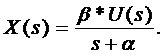
Представим схему конструируемой САР в общем виде в виде схемы:

Рис. 9.1. САР стабилизации угловой скорости
где передаточная функция объекта регулирования имеет вид:
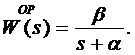
В качестве регулятора возьмем безынерционное звено с передаточной функцией:
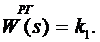
Задача синтеза стабилизирующего управления предполагает определение значения k1, при котором выполняется первая теорема Ляпунова. На этом и будет строиться решение. Для этого найдем передаточную функцию САР, получим:
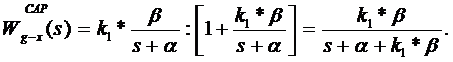
Для асимптотической устойчивости САР необходимо, чтобы корень характеристического уравнения был отрицательным, т. е.
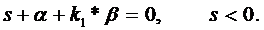
Что выполнимо, если
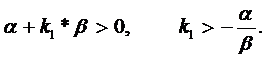 (9.16)
(9.16)
Вспомним, что по условию задачи ![]() - известные константы. Характеристическое уравнение САР имеет вид:
- известные константы. Характеристическое уравнение САР имеет вид:
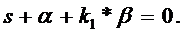
Поскольку по нему уже было принято решение для обеспечения устойчивости САР, воспользуемся им и подставим вместо k1 величину ![]() с учетом (9.16), при условии, что
с учетом (9.16), при условии, что 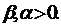 Подставим полученные результаты в U(t), которая согласно схеме имеет вид:
Подставим полученные результаты в U(t), которая согласно схеме имеет вид:
![]()
| (9.17) |
Подставим (9.17) в (9.15). Будем иметь:
| (9.18) |
Откуда следует, что для стабилизации управления достаточно обеспечивать уравнение динамики вида:
![]()
Система, поведение которой описывается таким уравнением, является асимптотически устойчивой, т. к. уравнение получено с учетом выводов первой теоремы Ляпунова.
Сравнение результатов двух независимых методик синтеза оптимального управления на данном примере показало, что поиск оптимального управляющего воздействия выполнен, но методика на основе моделирования процессов в s - области выглядит более значимой с точки зрения придания САУ желаемых свойств. Поскольку помимо устойчивости методика позволяет устанавливать требуемое быстродействие, а если в качестве математической модели динамики рассматривать не характеристическое уравнение, а передаточную функцию, то и точность управления. Вторым важным моментом сравнения следует отметить элементарность расчетов и, следовательно, их наглядность и высокую точность.
Задача 9.2. Рассмотрим задачу оптимальной стабилизации [8] для системы вида
| (9.19) |
К системе уравнений (9.19) применим преобразование Лапласа, получим:
| (9.20) |
Найти вид стабилизирующего управления u(t) = - F*x(t).
Решение 1. Применим методику моделирования процессов в s - области [6-7]. Построим схему для уравнений (9.20).
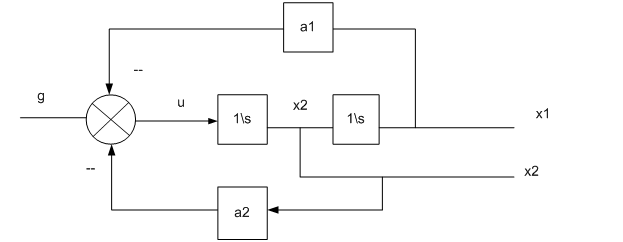
Рис. 9.2. САР оптимальной стабилизации
В схему в обратные связи добавлены безынерционные звенья с параметрами а1 и а2 соответственно, выполняющие функции управления за счет перенастройки параметров.
Найдем передаточные функции от входа к выходам, получим:
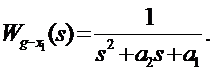
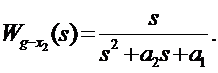
Выпишем характеристическое уравнение:
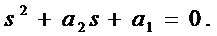
Его можно представить: (s-s1) * (s-s2) = 0,
где s1, s2 - корни уравнения. Положим корни эталонной САР равными s1 = s2 = -1. Тогда характеристическое уравнение примет вид:
(s + 1) * (s + 1) = s2 + 2s + 1 = 0.
Сформируем целевую функцию на основе минимизации среднеквадратичной ошибки аппроксимации. Запишем
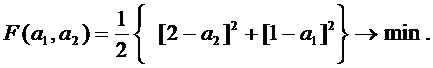
Для того, чтобы реальная САР (рис. 9.2) работала устойчиво, достаточно, чтобы а1 = 1 , а2 = 2.
Найдем U(s) по схеме рис. 9.2, будем иметь:
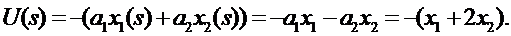
Проанализируем качество синтезированной САР по расположению корней характеристического уравнения. Будем иметь:
· степень устойчивости -
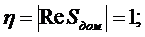
· колебательность процессов -
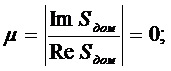
· время переходного процесса –
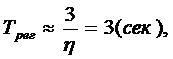 при статической ошибке
при статической ошибке ![]()
Для поиска решения на основе моделирования процессов в s - области потребовалось выполнение следующих действий:
· применить преобразование Лапласа к исходной системе
уравнений;
· построить функциональную схему САР, введя регулятор в
контур управления;
· найти характеристическое уравнение САР;
· задать эталонные корни характеристического уравнения с
учетом требования устойчивости;
· по эталонным корням восстановить характеристическое
уравнение эталонной САР;
· построить целевую функцию F(x);
· решить задачу оптимизации, т. е. найти оптимальные
значения параметров регулятора а1, а2;
· проанализировать динамику САР, работающую согласно
синтезированному управлению.
Решение 2. Рассмотрим решение поставленной задачи на основе применения уравнения Риккати. В качестве критерия оптимальности выберем функционал [8]:
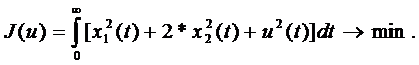
Будем искать вид стабилизирующего управления по форме:
u(t) = - F*x(t).
Применим уравнение Риккати. Определим расчетные матрицы:
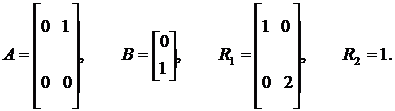
Подставим их в уравнение (9.5), получим:
|
Сложим элементы матриц друг с другом, соблюдая порядок равенства индексов элементов матриц. Составим уравнения на основе приравнивания к нулю элементов матрицы, получим:
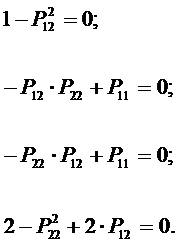
Анализ уравнений показывает, что второе и третье уравнения совпадают. Поэтому оставим только три линейно независимых уравнения, получим:
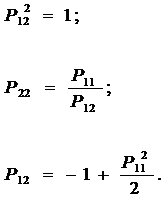
Как показывает анализ, имеем дело с системой нелинейных алгебраических уравнений, которая может быть решена численным градиентным методом. Чтобы его применить, обозначим переменные следующим образом:
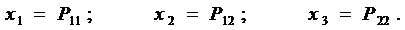
Составим целевую функцию в виде:
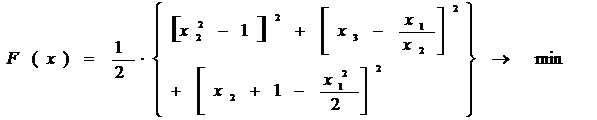
Минимизация целевой функции позволила получить следующий результат:
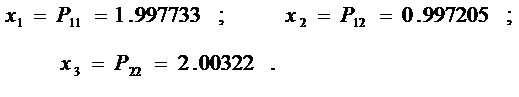
Если результат округлить с точностью до 0.003, получим:
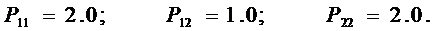
Проверка ручного счета с помощью пакета программ matcad, позволила получить те же результаты:
|
Поставим полученную матрицу в формулу (9.4), будем иметь:
|
Подставим последнюю формулу в (9.3), получим:
|
Решение этой же задачи другим известным QR-алгоритмом, опирающимся на уравнение Риккати, дало аналогичный результат [8].
Таким образом, оптимальное управление будет обеспечиваться согласно полученному закону. Отметим, что для проверки ручного счета было сделано обращение к пакету стандартных математических программ matcad, что удобно в проектировании, но неудобно в процессе выработки оптимального управления в режиме реального времени.
В плане недостатков работы с методами синтеза оптимального управления на основе уравнения Риккати или на основе QR - алгоритма следует отметить работу с символьными матрицами. В них алгебраические вычисления, согласно предложенным методикам, ведутся в направления умножения, сложения, вычитания символьных матриц, что требует больших вычислительных затрат, особенно когда размерность матриц более двух. Кроме того решение полученных уравнений в общем случае нелинейных может вообще не дать результат в области действительных чисел. Синтез же оптимального управления на основе моделирования процессов в s – области всегда дает удовлетворительное решение.
10. Общие принципы построения моделирующих алгоритмов
При реализации моделирующих алгоритмов на цифровых машинах есть определенные общие закономерности.
Основная проблема при составлении алгоритмов на машине с последовательной обработкой процессов состоит в том, что при моделировании необходимо отслеживать множество процессов, которые в реальном времени происходят параллельно. В связи с этим алгоритмы моделирования имеют свои особенности:
- продвижение системы во времени, отслеживание временной координаты; обеспечение синхронной работы объектов, из которых состоит моделируемая система.
В настоящий момент известны четыре основных принципа регламентации событий.
1. Принцип Δt.
2. Принцип особых состояний.
3. Принцип последовательной проводки заявок.
4. Принцип параллельной работы объектов (объектный принцип моделирования).
Рассмотрим на примерах, как реализуется в моделирующих алгоритмах каждый из принципов.
10.1. Принцип Δt
Принцип состоит в том, что алгоритмом моделирования имитируется движение, то есть изменение состояния системы в фиксированные моменты времени: t, t + Δt, t + 2Δt, t + 3Δt, …
Для этого заводится счетчик времени, который на каждом цикле увеличивает свое значение на величину шага во времени Δt, начиная с нуля (начало моделирования). Таким образом, изменения системы отслеживаются такт за тактом в заданные моменты: t, t + Δt, t + 2Δt, t + 3Δt, …
Этот принцип является наиболее универсальным, так как применим для широкого класса систем. Он же является и наиболее простым в реализации.
Однако это самый неэкономный принцип, поскольку вся система анализируется моделирующим алгоритмом на каждом такте, даже если в ней не происходит никаких изменений.
Другой недостаток состоит в том, что времена событий округляются до величины Δt, что ведет к погрешностям в определении переменных, характеризующих систему.
Пример. Моделируется склад изделий с максимальной емкостью G (см. рис. 10.1).
| |
Рис. 10.1. Схема моделируемой производственной системы |
Склад принимает изделия от трех поставщиков (обозначим номера входных потоков изделий 1, 2, 3) и выдает их трем потребителям (обозначим номера выходных потоков изделий 4, 5, 6). Примем в качестве характеристики каждого входа интенсивность i - го потока изделий λi. Интенсивность характеризует в среднем интервал между двумя моментами времени прихода (ухода) изделий на склад. Обозначим через Pi размер партии изделий, уходящих или приходящих на склад. То есть этими переменными мы определили, когда и сколько приходит или уходит изделий на тот или иной вход или выход склада.
Обозначим переменной Z текущее количество изделий на складе. Если изделия приходят на склад (потоки 1, 2, 3), то Z увеличивается на P1, P2 , P3. Если изделия изымаются со склада (потоки 4, 5, 6), то Z уменьшается на P4, P5 , P6. То есть Z играет роль счетчика изделий, находящихся на складе в отдельные моменты времени t. Начальное состояние склада на момент t := 0 примем равным Z0.
Алгоритм построим таким образом, чтобы вычислить вероятности событий возникновения дефицита Pд и переполнения Pп на складе.
Для накопления надежной статистики эксперимент повторим KK раз. За количеством экспериментов следит счетчик экспериментов k. Каждый эксперимент длится от 0 до Tk . Счетчик времени t отсчитывает время от 0 до Tk с дискретностью Δt .
В каждом эксперименте подсчитывается, сколько раз на складе в результате действия входных сигналов (количество поставленных и изъятых изделий) возникает ситуация дефицита. За этим следит счетчик D, если на складе возникает ситуация Z < 0 значит, возникает дефицит изделий для обработки и счетчик D увеличивает свое значение на 1. Если дефицит не возникает Z ≥ 0, то счетчик своего значения не меняет.
Поскольку всего может быть рассмотрено N := Tk / Δt тактов, то вероятность возникновения дефицита может быть примерно оценена частотой возникновения этих событий как Pд := D/N или с учетом того, что счетчик D накапливался в течении KK экспериментов, то Pд := D/N/KK или Pд := D / (N*KK), или Pд := D · Δt / (Tk*KK). Расчет вероятности переполнения склада моделируется аналогично (учитывается, что переполнение возникает, когда Z становится больше емкости склада G) .
Заметим, что поскольку на складе в реальности не может быть изделий меньше нуля, то значение Z в момент обнаружения этого факта должно быть возвращено на ближайшую границу, то есть: Z := 0. То же самое касается ситуации переполнения (Z := G).
Алгоритм представляет сбой цикл по времени от 0 до Tk с шагом Δt — моделирование производится во времени. В каждом цикле (на каждом такте времени) проверяется, лежит ли сгенерированное Ti событие в интервале времени [T, T + Δt]: T ≤ Ti < T + Δt. Если событие происходит в данный момент, то определяется, какой i - ый входной сигнал предопределил это событие, обрабатывается ситуация и генерируется время следующего события. Проверка на каждом такте происходит по всем возможным входным и выходным сигналам.
| |
Рис. 10.2. Блок-схема алгоритма, реализованного по принципу Δt |
Рассмотрим алгоритм в виде записи последовательности действий, легко представимой в виде программного кода:
1. Инициализация: ![]() k = 0.
k = 0.
2. k <= KK? Если нет, то переход к п. 17.
3. Z = Z0. T[1] = T[2] = … = T[6] = 0; T = 0; Tk = 0.
4. T <= Tk ? Если нет, то k = k +1, переход к п. 2.
5. i = 1.
6. i <= 6 ? Если нет, то переход к п. 13.
7. T[i] <= T + ![]() ? Если нет, то переход к п. 12.
? Если нет, то переход к п. 12.
8. i <= 3 ? Если да, то Z = Z + P[i], переход к п. 10.
9. Z = Z – P[i].
10. Генерация случайного числа r.
11. 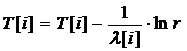 .
.
12. i = i + 1, переход к п. 6.
13. T = T + ![]() .
.
14. Z < 0? Если да, то D = D + 1; Z = 0, переход к п. 4.
15. Z > G? Если нет, то переход к п. 4.
16. n = n + 1; Z = G, переход к п. 4.
17. 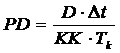
18. 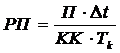
19. Вывод PD, PП.
20. Конец алгоритма.
10.2. Принцип особых состояний
Назовем состояние, в котором обычно находится система, обычным состоянием. Такие состояния интереса не представляют, хотя занимают большую часть времени.
Особые состояния — это такие состояния в изолированные моменты времени, в которых характеристики системы изменяются скачкообразно. Для изменения состояния системы нужна определенная причина, например, приход очередного входного сигнала. Ясно, что с точки зрения моделирования интерес представляет именно изменение характеристик системы, то есть принцип требует отслеживать моменты перехода системы из одного особого состояния в другое.
По сравнению с предыдущим случаем, мы не будем проверять изменение состояния системы в каждый момент времени. Выберем среди будущих моментов только тот, в который происходит поступление или уход изделий со склада, ближайший к текущему моменту времени. Определив такой момент, сразу перейдем в него скачком, изменив значение счетчика времени на величину (–Ln(r)/λi). В остальном, алгоритм похож на предыдущий. Заметим только, что по сравнению с предыдущим алгоритмом цикл опроса входных сигналов ликвидирован, поскольку соответствующий блок четко отвечает на вопрос, какой из i - ых сигналов имел место.
Такой принцип существенно экономит время моделирования.
| |
Рис. 10.3. Блок-схема алгоритма принципа особых состояний |
Рассмотрим алгоритм в виде записи последовательности действий, легко представимой в виде программного кода:
1. Инициализация: ![]() k = 0.
k = 0.
2. k <= KK? Если нет, то переход к п. 9.
3. Z = Z0. T[1] = T[2] = … = T[6] = 0; T = 0.
4. ![]()
5. T <= Tk ? Если нет, то k = k +1, переход к п. 2.
6. i <= 3 ? Если да, то Z = Z + P[i], Z > G? Если да, то П = П + 1; Z = G.
Переход к п. 7
Если нет, то Z = Z – P[i]; Z < 0? Если да, то D = D + 1; Z = 0.
7. Генерация случайного числа r.
8. 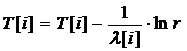 , переход к п. 4.
, переход к п. 4.
9. 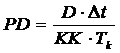
10. 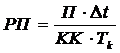
11. Вывод PD, PП.
12. Конец алгоритма.
10.3. Принцип последовательной проводки заявок
Принцип состоит в том, что каждая заявка отслеживается от момента поступления ее в систему до момента ее выхода из системы. И только потом рассматривается следующая заявка.
Рассмотрим работу алгоритма на примере двухканальной системы массового обслуживания заявок с двумя местами в общей очереди и отказами при переполнении очереди (см. рис. 10.4).
| |
Рис. 10.4. Схема системы массового обслуживания с двумя каналами и ограниченной очередью |
Обозначим: λi — интенсивность прихода заявки; μi — интенсивность обслуживания заявки.
Построим алгоритм, определяющий вероятности обслуживания заявок и отказа заявок, а также пропускную способность системы.
Чтобы понять работу алгоритма, представим для наглядности параллельные линейки — оси времени для каждого из мест, в которых может оказаться заявка в процессе обслуживания. Генерируем заявку (блоки 3, 4 — здесь и далее см. блоки на рис. 10.6). Случайный момент времени, когда заявка пришла в систему, равен Tс. Время между двумя случайными заявками имитируется формулой τ := –1/λ · ln(r), которое прибавляется к Tс предыдущей заявки Tс := Tс – 1/λ · ln(r). Учтем этот факт в счетчике пришедших заявок N (блок 4).
Последовательно сравниваем Tс в порядке приоритетов (блоки 5, 6, 7, 8) с временами освобождения T1 канала 1, канала 2 — T2, места в очереди 1 — T3, места в очереди 2 — T4. Как только обнаруживается факт того, что место в системе свободно (см. рис. 10.5): Tс > T1 или Tс > T2, или Tс > T3, или Tс > T4, так немедленно переводим заявку на свободное место и имитируем обработку ее на этом месте.
| |
Рис. 10.5. Механизм определения освобождения канала |
Допустим, что освободилось место в первом канале. Обработка состоит в том, что вычисляется время простоя этого канала до прихода заявки (например, Tс – T1), и это время прибавляется в счетчик времен простоя (блок 15). Вычисляется следующее время изменения состояния канала — модифицируется переменная T1, которая укажет нам в дальнейшем, когда снова освободится канал. Величина T1 изменяется на величину τ := –1/μ1 · ln(r) — время обслуживания, отсчитываемое от начала обслуживания Tс. Счетчик обслуженных заявок Nоб увеличивается на единицу.
Аналогично обработка происходит и во втором канале, если заявка попадет именно туда (блок 14).
Особенность обработки заявки в очереди состоит в том, что первое место в очереди освобождается, когда освобождается место в одном из каналов, конечно, заявка уходит туда, где место освобождается раньше (блоки 5, 6). Второе место в очереди освобождается одновременно с первым, так как заявка в очереди передвигается на первое освободившееся место (блок 12).
Далее алгоритм генерирует в цикле следующую заявку (блоки 3, 16). Остановка моделирования происходит тогда, когда каждая линейка будет заполнена до момента Tk (блок 16). После этого происходит обработка статистических результатов, накопленных в счетчиках (блок 17). Вероятность оценивается частотою появления события, она вычисляется как отношение количества появившихся событий к количеству возможных появлений.
Блок - схема алгоритма показана на рис. 10.6.
| |
Рис. 10.6. Блок-схема алгоритма последовательной проводки заявок |
Следует помнить, что чем больше время моделирования, тем точнее полученный результат и как только статистическая величина перестает меняться в пределах объявленной точности, то есть кривая входит в коридор, отведенный ей точностью, то это сигнализирует о достаточности количества экспериментов.
Необходимо внимательно следить, чтобы все искомые переменные вошли в интервал объявленной точности, только тогда можно прекратить моделирование и быть уверенным в результате.
10.5. Объектный принцип моделирования
Как правило, алгоритмы, спроектированные по первым трем принципам, плохо модернизируются. А производственная ситуация часто меняется и требует соответствующих моделей для нахождения рациональных решений в процессе управления.
Таким образом, возникает необходимость в приемах моделирования, обеспечивающих независимость составления моделей элементов сложной системы от изменения задачи или структуры производства. Такой подход моделирования отдельных объектов независимо друг от друга позволяет собирать сколь угодно сложные системы без изменения их составляющих. Принцип объектного моделирования обеспечивает модернизацию сложных систем, удлиняя жизненный цикл АСУ.
Пример. СМО состоит из следующих элементов: источник заявок, очередь, канал (см. рис. 10.7). Смоделируем их по отдельности.
| |
Рис. 10.7. Схема реализации объектно-ориентированного моделирования (на примере СМО) |
1. Источник заявок (Sourcer) генерирует последовательность случайных событий.
2. Канал обслуживания (Channel).
3. Очередь (Queue).
4. Статистика (Stats).
Данные модели могут собираться в любые конфигурации без изменения их содержания.
11. Имитация случайных процессов
Случайной называется функция, ординаты которой для любых фиксированных значений аргумента являются случайными величинами (СВ). Задачу моделирования случайных функций в общем случае нельзя свести к имитации СВ для каждого значения аргумента, так как между ординатами существует корреляционная зависимость. Случайная функция, аргументом которой является t - время, носит название случайного процесса (СП).
Целью имитационного моделирования СП на ЭВМ является воспроизведение различного рода сигналов и помех. Нужно иметь в виду, что воспроизведение на ЭВМ процессов с непрерывным временем невозможно ввиду дискретной природы ЭВМ. Задача моделирования СП в дальнейшем понимается как задача отыскания алгоритма, позволяющего формировать на ЭВМ реализации СП.
СП считается заданным, если заданы функции: дисперсии d(t), математического ожидания m(t) и корреляционная функция k(ti, tj). Эти функции являются неслучайными, их определяют путем обработки опытных данных методами математической статистики.
11.1. Имитация нестационарных случайных процессов
Рассмотрим алгоритм канонических разложений, пригодный как для стационарных, так и нестационарных СП, предложенный .
Пусть F(t1), F(t2), . . . F(tn) - реализация СП на конечном интервале времени Т, тогда в соответствии с методом:
![]()
![]()
![]()
Здесь х1, х2, . . . хn - значения случайных, некоррелированных СВ с заданным законом распределения; ![]() - координатные функции, обладающие свойствами:
- координатные функции, обладающие свойствами:
а) ![]() = 0 при i > j;
= 0 при i > j;
б) ![]() = 1.
= 1.
Координатные функции и дисперсии Di величин 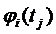 можно вычислить в соответствии с рекуррентными уравнениями:
можно вычислить в соответствии с рекуррентными уравнениями:

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 |




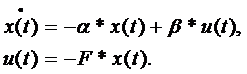
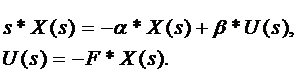
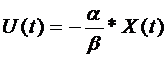
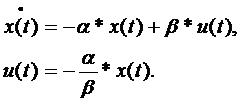
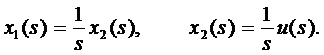
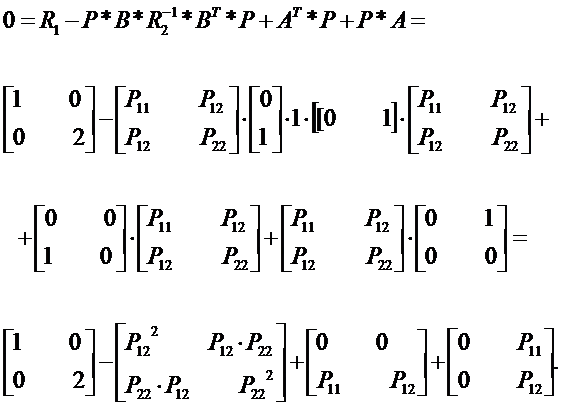
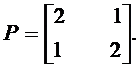
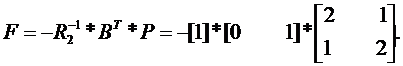
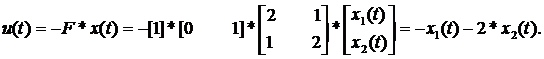
![[ Рис. 32.1. Схема моделируемой производственной системы (пример) ]](/text/78/388/images/image274_0.png)
![[ Рис. 32.2. Блок-схема алгоритма, реализованного по принципу ?t. Пример — моделирование производственного склада ]](/text/78/388/images/image275.jpg)
![[ Рис. 32.3. Блок-схема алгоритма, реализованного по принципу особых состояний. Пример — моделирование производственного склада ]](/text/78/388/images/image282.jpg)
![[ Рис. 32.4. Схема системы массового обслуживания с двумя каналами и ограниченной очередью ]](/text/78/388/images/image285.jpg)
![[ Рис. 32.5. Механизм определения освобождения канала (иллюстрация) ]](/text/78/388/images/image286.png)
![[ Рис. 32.6. Блок-схема алгоритма, реализованного по принципу последовательной проводки заявок. Пример — моделирование системы массового обслуживания ]](/text/78/388/images/image287.jpg)
![[ Рис. 32.7. Схема реализации объектно-ориентированного моделирования (на примере СМО) ]](/text/78/388/images/image288.png)
