На правах рукописи
МОДЕЛИРОВАНИЕ ПРОЦЕССОВ среднесрочного прогнозирования землетрясений в районе Восточного Предкавказья
05.13.18. Математическое моделирование, численные методы и
комплексы программ
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата технических наук
Махачкала – 2009
Работа выполнена в ГОУ ВПО «Дагестанский государственный
технический университет»
Научный руководитель: кандидат технических наук, доцент
Гаджиев Аюб Акбашович
ОФИЦИАЛЬНЫЕ ОППОНЕНТЫ:
доктор физико-математических наук, профессор Назаралиев Магомед-шафи Ахмедович
кандидат технических наук, доцент Канаев Магомедимин Муталимович
Ведущая организация: Дагестанский научный центр РАН
Защита состоится «__ » _______ 2009г. в ___час.____мин. на заседании диссертационного совета Д 212.052.03, при ГОУ ВПО «Дагестанский государственный технический университет» по адресу г. Махачкала, пр. Имама Шамиля, ауд. 202
С диссертацией можно ознакомиться в библиотеке ГОУ ВПО «Дагестанский государственный технический университет»
Автореферат разослан «____» ______2009г.
Ученый секретарь
диссертационного совета
Общая характеристика работы
Актуальность исследования. Внезапность и непредсказуемость стихийных бедствий влекут за собой многочисленные человеческие жертвы и огромный материальный ущерб. Современные карты сейсмического и микросейсмического районирования дают представление о месте и силе возможного землетрясения. Что касается прогноза времени землетрясения, то для современной науки данный вопрос пока остается открытым. Поэтому проблема разработки математических моделей и основанных на них методов прогнозирования времени землетрясений является актуальной.
Сейсмический режим как Земли в целом, так и отдельного локального сейсмоактивного участка земной коры определяется множеством случайных независимых друг от друга факторов и трудностью и неоднозначностью условий получения информации о геофизических процессах в очаговой зоне, обусловленных изменчивостью структуры и физических свойств среды. Как следствие этого, существующие физические и математические модели пока еще не позволяют адекватно решать проблемы прогнозирования землетрясений. Речь идет о реологических моделях, описывающих упругие и пластические деформации твердого тела, и математических моделях в конечных разностях. Эти модели гомоморфны, и не учитывают все нюансы и аспекты возникновения и развития сложных геофизических процессов в земной коре.
Отмеченные выше обстоятельства и обусловили цель и задачи настоящего диссертационного исследования.
Объектом исследования является сейсмическая активность района Восточного Предкавказья, которая представляет собой сложное явление, протекающее в неоднородной физической структуре, поведение которой носит случайный характер и зависит от множества сейсмогенерирующих факторов.
Предмет исследования – математическое моделирование причинно-следственных связей между сейсмогенерирующими факторами и их влияния на проявления событий, связанных с землетрясениями.
Цель и задачи диссертационного исследования – разработка моделей прогнозирования времени землетрясения на локальном участке земной коры (на примере района Восточного Предкавказья).
В соответствии с поставленной целью решаются следующие задачи:
- определить факторы, генерирующие сейсмическую активность исследуемого района;
- сформировать математическую модель причинно-следственных связей между сейсмогенерирующими факторами и сейсмической активностью;
- исследовать влияние каждого фактора на сейсмическую активность Восточного Предкавказья и ранжировать факторы по степени их влияния на сейсмическую активность при комплексном рассмотрении проблемы;
- формализовать процессы взаимодействия факторов и их влияние на объект исследования;
- разработать модель прогнозирования сейсмической активности региона;
- разработать программный комплекс, позволяющий реализовать предложенные методы и модели прогнозирования сейсмической активности.
Основные положения, выносимые на защиту.
1. Метод ранжирования сейсмогенерирующих факторов по степени влияния на сейсмическую активность при комплексном их рассмотрении.
2. Алгоритм вычисления функций принадлежности сейсмогенерирующих факторов к нечетким подмножествам факторов влияния на сейсмическую активность.
3. Математическая модель прогнозирования сейсмической активности локального участка земной коры, разработанная на основе математического аппарата нечетких множеств и нечеткой логики.
Научная новизна заключается в разработке оригинальных алгоритмов и математических моделей, позволяющих ранжировать сейсмогенерирующие факторы, получить количественные оценки степени их влияния на сейсмическую активность и на этой основе спрогнозировать события, сопровождающиеся землетрясением.
К основным результатам, представляющим новизну исследования, можно отнести следующие:
– разработан и исследован алгоритм ранжирования сейсмогенерирующих факторов по степени их влияния на сейсмическую активность на основе метода эвристической самоорганизации (массовой селекции), который позволяет получить количественные оценки степени влияния каждого фактора на сейсмическую активность;
– разработан алгоритм для вычисления функции принадлежности сейсмогенерирующих факторов к нечетким подмножествам факторов влияния на сейсмическую активность, отличительной особенностью которого является снижение фактора субъективности на этапе определения принадлежности исходных фактических значений (статистических данных) к заданным нечетким подмножествам, что позволяет повысить точность решений задач прогнозирования;
– установлена противофазная закономерность причинно-следственной связи «сейсмогенерирующие факторы – сейсмическая активность»;
– предложена модель прогнозирования времени землетрясений, позволяющая строить среднесрочные прогнозы сейсмической активности в районе Восточного Предкавказья, с учетом комплексного влияния сейсмогенерирующих факторов на его сейсмическую активность;
– разработан комплекс моделирующих программ, позволяющий исследовать предложенные алгоритмы и строить достоверные прогнозы.
Практическая ценность полученных результатов:
Основные научные результаты были использованы при построении информационных систем среднесрочного прогнозирования землетрясений в Республике Дагестан, программная реализация которой внедрена на сейсмической станции «Махачкала».
Апробация работы. Основные научные результаты диссертационной работы докладывались и обсуждались на IV российско-украинском научно-техническом и методическом симпозиуме (Пенза, 2006), на III Всероссийской конференции по актуальным проблемам внедрения и развития сектора IT-технологий «Современные информационные технологии в проектировании, управлении и экономике» (Махачкала, 2008).
Публикации. По результатам диссертационной работы опубликовано 5 печатных работ, в том числе 1 работа в издании, рекомендованном ВАК.
Структура и объем работы. Диссертационная работа состоит из введения, четырех глав и заключения, изложенных на 137 страницах, содержит 22 рисунка, 31 таблицу и 43 страницы приложения. Список литературы содержит 54 наименования.
КРАТКОЕ СОДЕРЖАНИЕ РАБОТЫ
Основные факторы, влияющие на сейсмическую активность района Восточного Предкавказья можно определить следующим образом:
1) глобальные, к которым относятся циклическое изменение солнечной активности (x1) и сложное циклическое движение Луны (x2), состоящее из движения по орбите вокруг Земли и вращения около собственной оси, которое определяет приливно-отливные процессы в атмосфере, гидросфере и твердом теле Земли;
2) межрегиональный фактор (x3), определяемый географическим расположением района Восточного Предкавказья и (с учетом теории литосферных плит) тектонофизикой, формируемой взаимодействием Евразийской (Русской) и Индо-Австралийской платформ с Аравийской, Иранской и Эгейско-Адриатической плитами;
3) региональный, к которому относятся, в первую очередь, колебания уровня Каспийского моря (x4).
4) климатологический фактор, который задается динамикой ледникового покрова Большого Кавказа (x5).
Необходимость учета приведенных выше факторов в системном прогнозировании можно обосновать следующим образом:
1. Солнце, Земля и Луна представляют собой три взаимосвязанных и взаимодействующих небесных тела, составляющих равновесную систему. Вследствие влияния Солнца и Луны Земля постоянно находится в движении и развитии, результатом чего являются, в первую очередь, тектонические процессы в твердом теле Земли.
2. Геологические исследования с помощью современных приборов показали, что земная кора состоит примерно из 20 малых и больших плит или платформ, постоянно изменяющих свое местонахождение на планете. Те места, где они соприкасаются между собой (разломы, швы), являются главными причинами землетрясений.
3. Исследования колебаний уровня моря представляют большой интерес для сейсмологической науки, так как находит подтверждение гипотеза о тесной связи между сейсмичностью Кавказа и уровенным режимом Каспия. Считается, что именно изменения уровня Каспия являются одним из сейсмогенерирующих факторов, а не наоборот.
4. Ледники представляют собой одно из наиболее мобильных звеньев общей геодинамической системы Кавказского региона. Как показывают наблюдения, снятие давления на земную кору приводит к тому, что уже через 5-25 лет происходит резкое изменение режима сейсмичности (в сторону его увеличения).
Анализ отмеченных выше факторов показывает необходимость создания банка статистических данных наблюдений за динамикой изменения этих факторов и их влияния на сейсмическую активность. В общем случае все факторы, характер их влияния и собственно сейсмическая активность представляют собой случайные, непрерывные процессы, имеющие разную физическую природу. По этой причине имеет смысл использование их приведенных значений, взяв за единицу максимальное значение ряда наблюдений в течение рассматриваемого промежутка времени.
Для нахождения относительных значений фактор-параметров, абсолютные значения которых могут быть как положительными, так и отрицательными, определяются приведенные их значения по следующей формуле:
![]() , (1)
, (1)
где min хi – минимальное значение i-го фактора.
Относительные значения факторов вычисляются по формуле:
![]() , (2)
, (2)
где xi – абсолютные значения i - го фактора;
ximax – максимальное значение i-го фактора в рассматриваемом интервале времени.
Такой подход приведения сейсмогенерирующих факторов для хранения в банке данных при определении их влияния на сейсмическую активность имеет свои особенности. Во-первых, модель данных является открытой и пополняется непрерывно. Это позволяет анализировать геофизическую обстановку в произвольные моменты времени и в зависимости от складывающейся ситуации. Во-вторых, следует учитывать то обстоятельство, что относительные значения следует пересчитывать лишь в том случае, если очередное текущее значение окажется больше, чем принятое значение ximax.
При этом динамика развития каждого из основных факторов с 1970 по 2005 год будет представлять собой следующую картину (см. рис. 1):
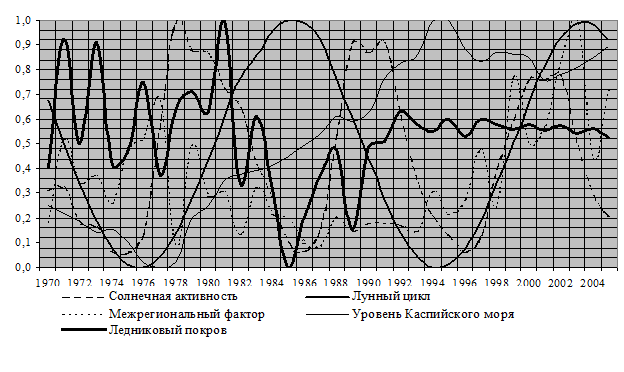
Рис. 1. Динамика развития сейсмогенерирующих факторов
На графиках, приведенных на рис. 1, наблюдается коррелированность солнечной активности и ледникового покрова, лунного цикла и уровня Каспийского моря.
На основе динамики изменения факторов формируются графики корреляционных функций, отражающие влияние сейсмогенерирующих факторов на сейсмическую активность. При этом коэффициенты корреляции сейсмогенерирующих факторов с сейсмической активностью определяются по следующей формуле:
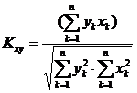 (3)
(3)
Для построения нормированных взаимно-корреляционных функций сейсмической активности района Восточного Предкавказья и сейсмогенерирующих факторов, используется следующее выражение:
(4)

![]()
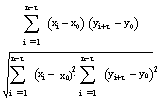

где xi – значения i-го фактора,
x0 – среднее значение фактора xi,
yi – значения выходного параметра,
y0 – среднее значение выходного параметра,
n – число реализаций,
τ – значение интервала (τ = 1 год).
Для прогнозирования сейсмической активности на основе полученных таким образом данных предложен метод, базирующийся на следующих основных положениях:
1) самоорганизация среды есть ключ к пониманию генезиса сейсмособытия;
2) в теории управления и теории распознавания образов известен ряд законов и принципов, основными из которых являются закон адекватности, закон необходимого разнообразия по У. Эшби и принцип внешнего дополнения;
3) декомпозиция сложной задачи прогнозирования землетрясений на ряд последовательно решаемых подзадач.
Для ранжирования сейсмогенерирующих факторов по степени их влияния на сейсмическую активность предложен метод эвристической самоорганизации (массовой селекции), который позволяет, учитывая равнозначное и совместное участие всех факторов одновременно и попарно, выявить значимость каждого из них в совокупном влиянии на сейсмическую активность.
Сущность метода эвристической самоорганизации заключается в следующем. Полное описание объекта – сейсмической активности – определяется функционалом:
![]() (5)
(5)
где x1, …, x5 - сейсмогенерирующие факторы,
у - сейсмическая активность локального участка земной коры (Восточного Предкавказья).
Полное представление объекта (5) в виде полиномиальной модели эвристической самоорганизации (массовой селекции) заменяется несколькими рядами частных описаний. В общем случае первый ряд селекции имеет вид:
![]() , (6)
, (6)
где s= C2n;
второй ряд селекции:
![]() , (7)
, (7)
где p=C2s, и т. д.
Для получения аналитической модели необходимо построить ряды селекции для каждого полученного уравнения селекции. Для этого ряд последовательности статистических данных по каждому фактору разбивается на обучающую и проверочную части. Обучающая последовательность используется для оптимизации значений коэффициентов уравнения регрессии. Обучающей является последовательность по нечётным годам, а проверочной - по чётным годам. В качестве структуры математической модели эвристической самоорганизации выбран квадратичный полином из шести членов с двумя аргументами.
Уравнения регрессии, полученные таким образом, обозначим yk* = f1(xi, xj) – обучающая система уравнений, yk** = f2(xi, xj) – проверочная система уравнений, где k изменяется от 1 до 10. Тогда для первого ряда селекции имеем (s=C25=10) систему из десяти уравнений (обучающая последовательность):
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ; (8)
; (8)
![]() ;
;
![]() ;
;
![]()
Для проверочной последовательности используем уравнения:
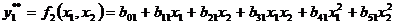 ;
;
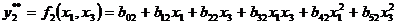 ;
;
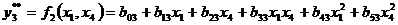 ;
;
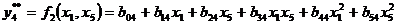 ;
;
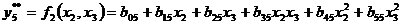 ;
;
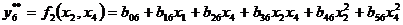 ;
;
![]() ; (9)
; (9)
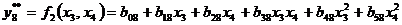 ;
;
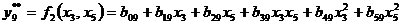 ;
;
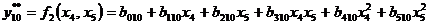 ;
;
Для каждого приведенного выше уравнения определяем коэффициенты при независимых переменных по имеющимся экспериментальным данным. Так, для уравнения
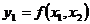
получаем следующую систему (для обучающей последовательности):
![]()
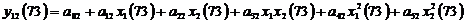
…
Аналогично для проверочной последовательности:
![]()

…
В системе уравнений (8) и (9) коэффициенты aij и bij вычисляются, подставив вместо y и хi их наблюдаемые значения из статистических рядов. Заметим, что при переходе от одного ряда к другому используются не все возможные, а только некоторое количество F самых лучших решений, найденных по некоторому критерию селекции. Как правило, выбирается F=n (n - число переменных х); в нашем случае F = 5.
Каждое из найденных уравнений регрессии оценивается по значению псм критерия несмещённости соответствующих коэффициентов aij (обучающей системы уравнений) и bij (проверочной системы уравнений) пары однотипных уравнений. Для первого ряда селекции формула критерия несмещённости коэффициентов имеет вид:
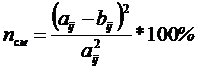 (10)
(10)
Из всех уравнений регрессии первого ряда селекции выбираем F=n=5 уравнений, имеющих меньшую оценку псм..
Критерий несмещённости решений для первого ряда селекции определяется как среднее значение показателя несмещённости коэффициентов для F отобранных несмещённых уравнений:
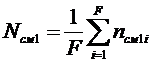 (11)
(11)
Второй ряд селекции строится аналогично. Критерий несмещённости
решений второго ряда имеет вид:
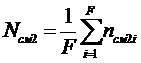 (12)
(12)
Данные формулы справедливы для третьего и последующих рядов селекции.
Ряды селекции наращиваются до тех пор, пока критерий несмещённости решений падает – Nсм→min. При достижении минимума несмещённости селекция останавливается во избежание её «вырождения».
Решение системы уравнений первого ряда селекции (8) и (9) позволило получить следующие результаты (см. табл. 1):
Таблица 1. Результаты первого ряда селекции
y | y1 | y2 | y3 | y4 | y5 | y6 | y7 | y8 | y9 | y10 |
Nсм1 | 28,4 | 5,9 | 66,9 | 12,6 | 0,01 | 8,5 | 3,6 | 9,3 | 376 | 14 |
По наименьшим значениям nсм1 отобраны уравнения y2, y5, y6, y7 и y8. Значение коэффициента несмещенности решений Nсм1=5,4.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 |




