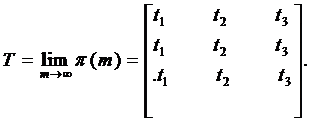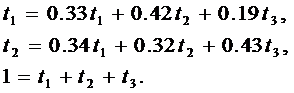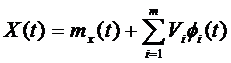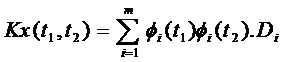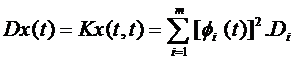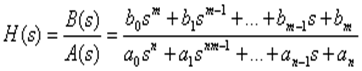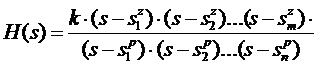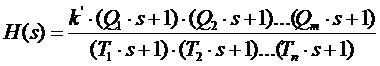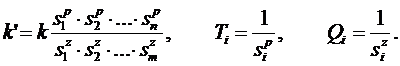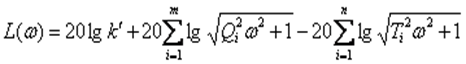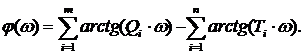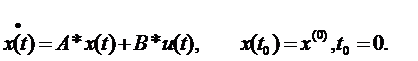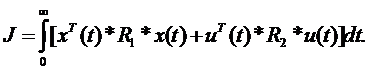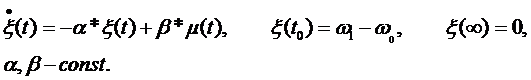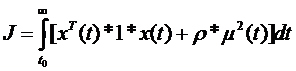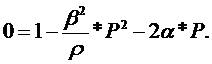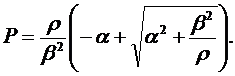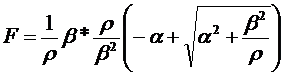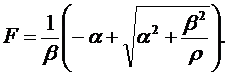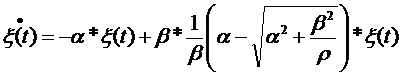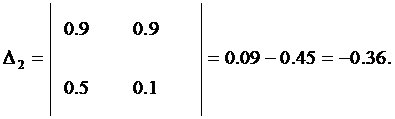
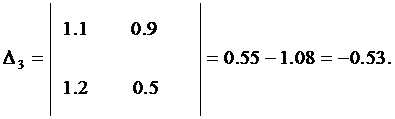
Используя найденные определители матрицы, получим:
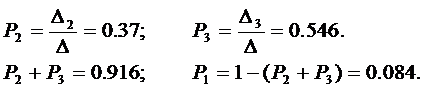
6.5. Определение матрицы M среднего времени перехода
Матрица М среднего времени перехода к некоторому состоянию из других состояний определяется соотношением:
| (6.13) |
Где
| (6.14) |
Здесь I – единичная матрица; π – матрица перехода; Т – матрица финальных вероятностей; E – единичная матрица (все элементы матрицы E равны единице); Zdg – матрица, получающаяся из матрицы Z обнулением вне диагональных элементов; D – диагональная матрица с элементами, равными обратным значениям элементов диагонали матрицы финальных вероятностей T.
Задача 6.3. Система может находиться в одном из трех состояний
![]()
Процесс в системе описывается цепью Маркова. Матрица перехода имеет вид:
| (6.15) |
Определить матрицу M.
Решение. Найдем первоначально матрицу финальных вероятностей
T вида:
| (6.16) |
Из (6.9) имеем для n = 3:
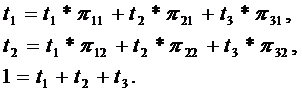
или
| (6.17) |
Решая систему алгебраических уравнений (6.17), получим:
![]()
Из (6.16) имеем:

Определим π − T , получим:
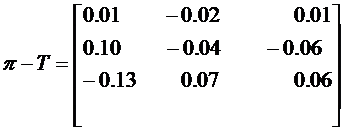
Определим матрицу I. Получим:
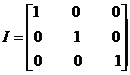
Найдем матрицу
![]()
Получим:

Определим матрицу Z. Получим:
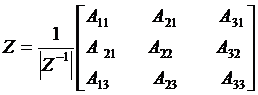
⎦
где
![]() – определитель матрицы
– определитель матрицы ![]() .
.
Здесь:
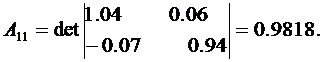
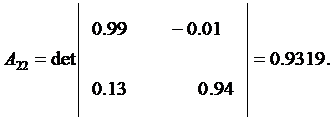

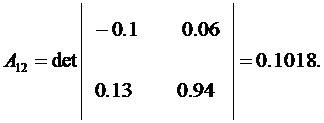
Матрица Z примет вид:

Определим матрицы I − Z, E * Z dg. Получим:
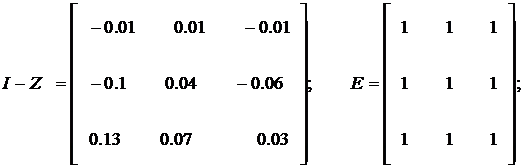

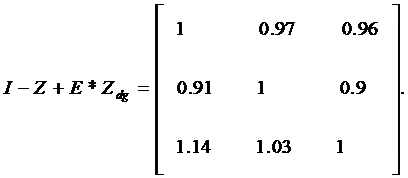
Опередим матрицу D. Получим:
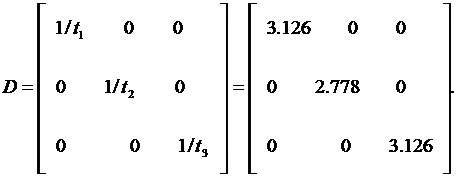
Определим матрицу M. Получим:
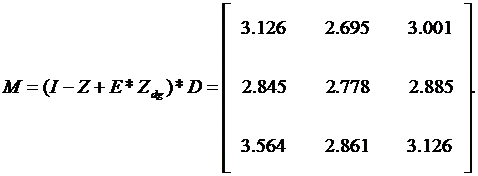
Каждый элемент полученной матрицы M характеризует среднее время
перехода из одного в другое соответствующее состояние. Так, время
перехода из первого в первое состояние в среднем равно 3,126 шага, из
первого во второе 2,695 шага, из первого в третье 3,001 шага и т. д.
7. Каноническое разложение случайного процесса
7.1. Теоретические сведения
Пусть случайный процесс X (t) представлен в виде:
| (7.1) |
где mx(t ) – математическое ожидание случайного процесса X (t ) ; ϕi (t ) –
неслучайные функции времени; Vi – случайные величины, причем:
M [Vi ] = 0; M [Vi*V j ] = 0, если i ≠ j
M [Vi2 ] = Di.
Здесь Di – дисперсия случайной величины Vi , m – количество неслучайных функций в каноническом разложении.
Соотношение (7.1) называется каноническим разложением случайного процесса X (t) .
Соотношению (7.1) соответствует корреляционная функция вида:
| (7.2) |
Соотношение (7.2) называется каноническим разложением корреляционной функции K x (t1 , t 2 ). Из (7.2) определим дисперсию Dx (t ) случайного процесса X (t) . Имеем:
| (7.3) |
7.2. Каноническое разложение случайного процесса в задачах
Задача 7.1. Пусть случайная функция X (t ) задана каноническим разложением:
X (t) = 3t + X1 ⋅ cos ωt + X 2 ⋅ sin ωt + X 3 ⋅ cos 2ωt + X 4 ⋅ sin 2ωt.
Случайные величины X 1 , X 2 , X 3 , X 4 имеют следующие математические ожидания и дисперсии:
m x1= m x 2 = m x 3 = m x 4 = 0; D x1 = D x 2 = 1; D x 3 = D x 4 = 3.
Определить m x (t), K x (t1 , t 2), Dx (t).
Решение. Прежде всего найдем m x (t ), получим:
M x (t) = 3t.
Определим K x (t1 , t 2 ). Будем иметь:
K x (t1 , t 2 ) = cos ωt1 ⋅ cos ωt2 + sin ωt1 ⋅ sin ωt 2 +
+ 3 cos 2ωt1 ⋅ cos 2ωt2 + 3 sin 2ωt1 sin 2ωt 2 =
= cos ω(t1 – t2 ) + 3 cos 2ω(t1 – t2 ).
Определим D x (t), получим:
Dx (t ) = K x (t, t) = 4.
Задача 7.2. Пусть случайная функция X (t) задана каноническим разложением вида:
X (t) = 2t + X 1 ⋅ sin t + X 2 ⋅ cos t.
Случайные величины X 1 , X 2 имеют следующие математические ожидания
и дисперсии:
m x1 = m x 2 = 0; D x1 = D x 2 = 3 .
Найти каноническое разложение случайной функции Y (t) вида:
Y (t ) = t ⋅ X (t) – t2 .
Определить m y (t ), K y (t1 , t 2 ), D y (t ).
Решение. Найдем каноническое разложение Y (t) . Будем иметь:
Y (t) = t 2 + X 1t ⋅ sin t + X 2t ⋅ cos t.
Определим m y (t). Получим: m y (t ) = t 2 . Найдем K y (t1 , t 2 ), получим:
K y (t1 , t 2 ) = 3t 1t 2 sin t 1 ⋅ sin t 2 + 3t 1t 2 cos t 1 ⋅ cos t 2 = = 3t 1t 2 cos(t 1 − t 2).
Определим D y (t), будем иметь:
D y (t) = K y (t, t ) = 3t 2 .
8. Идентификация динамических объектов
8.1. Общие положения идентификации математических моделей
Идентификация динамических объектов в общем случае состоит в определении структуры и параметров объектов по наблюдаемым данным – входному воздействию и выходным величинам.
В таком случае объект (элемент системы, объект управления, элемент технологического процесса и т. п.) представляет собой "черный ящик". Исследователю необходимо, подвергая объект внешним воздействиям и анализируя его реакцию, получить математическую модель (описание его структуры и параметров), то есть превратить "черный ящик" в "белый ящик", добиться его "информационной прозрачности". Графически процесс идентификации иллюстрирует рис. 8.1.
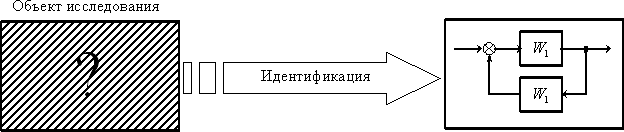
Рис. 8.1.
Важным моментом этого процесса является выбор точек приложения внешних воздействий и сбор информации о реакциях объекта, то есть размещение задающих устройств, датчиков.
Решается при идентификации объектов и более простая задача - задача идентификации параметров, когда заранее известна структура системы и ее математическая модель, но не известны все ее параметры. В этом случае говорят о переходе от "серого ящика" к "белому ящику". Графически процесс идентификации параметров иллюстрирует рис. 8.2.
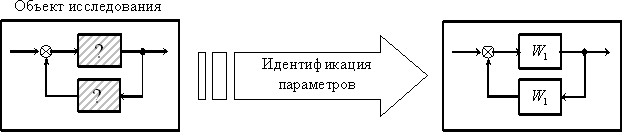
Рис. 8.2.
Задача идентификации параметров может либо входить компонентом в общую задачу идентификации объекта, либо решаться самостоятельно.
Рассмотрим на обобщенной структуре основы подхода к решению задач идентификации. Обобщенная структура процесса идентификации показана на рис. 8.3.
8.2. Обобщенная процедура идентификации
Идентификация объекта предполагает выполнение следующих этапов:
· Классификация объекта.
· Выбор для определенного класса объекта настраиваемой модели.
· Выбрать критерий качества идентификации, характеризующий отличие модели и объекта.
· Выбрать алгоритм идентификации (механизм настройки модели), обеспечивающий сходимость процесса идентификации, минимум критерия качества идентификации.
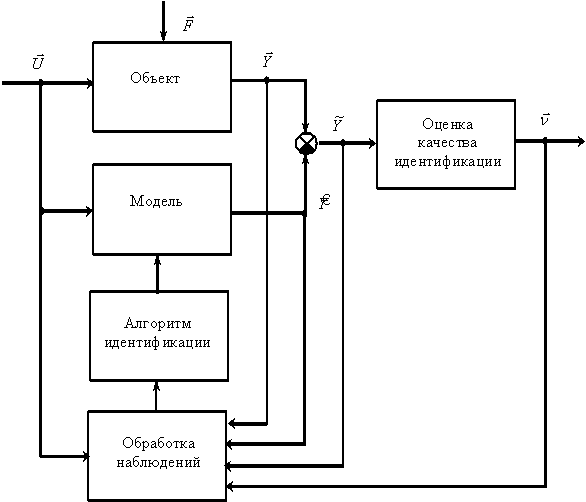
Рис. 8.3
Методы идентификации принято разделять на две группы:
· активная идентификация – идентификация вне контура управления,
· пассивная идентификация – идентификация в контуре управления.
Активная идентификация
В случае активной идентификации объект исследования выводится из условий нормальной окружающей среды (нормального режима эксплуатации). Исследования проводятся в специализированных лабораторных условиях, как это показано на рис. 8.3. На входы объекта (рабочие и дополнительные) подаются тестовые сигналы специального вида. Это могут быть:
· ступенчатые или импульсные временные сигналы;
· гармонические сигналы;
· случайные воздействия с заданными параметрами.
Активную идентификацию используют при разработке новых технологий применительно к действующим промышленным объектам, в изучении новых явлений, в первоначальной разработке математической модели.
Пассивная идентификация
При пассивной идентификации объект функционирует в контуре управления, находится в процессе нормальной эксплуатации. На его входы поступают только естественные сигналы управления. Пассивную идентификацию используют для уточнения математической модели, для слежения за изменениями в объекте. Информация оперативно используется в системе управления объектом, процесс такой идентификации иллюстрируется рис. 8.4.
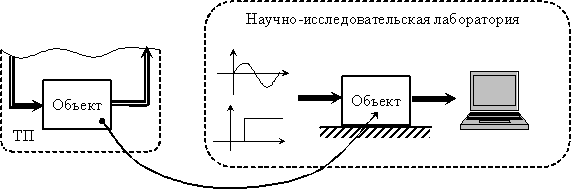
Рис. 8.4
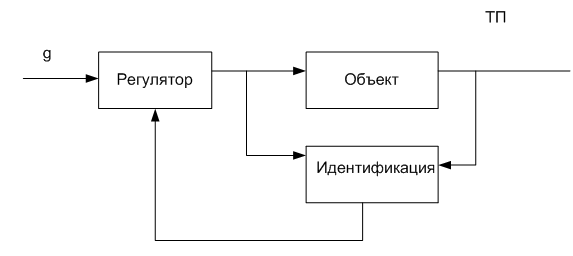
Рис.8. 5
Кроме перечисленных методов реализуются и системы идентификации смешанного типа, когда объект не выводится из нормального режима эксплуатации, но к управляющим сигналам добавляются тестовые воздействия, позволяющие идентифицировать объект, не ухудшая качества основного процесса управления.
Рассмотрим активную идентификацию более подробно. Активная идентификация объектов управления может производиться как во временной области, так и в частотной области. При этом в каждой области используют собственные алгоритмы и методы идентификации.
При активной идентификации в большинстве случаев используют полученные в результате экспериментов характеристики:
· частотные характеристики (АФЧХ, ЛАЧХ, ЛФЧХ и др.);
· временные характеристики (переходные, весовые и др.).
Рассмотрим в качестве примера один из подходов решения задачи идентификации структуры и параметров объекта в частотной области. Ограничим рассмотрение объектом с одним входом и одним выходом.
Известно, что если имеется математическая модель такого объекта в виде передаточной функции:
| (8.1) |
то это соответствует наличию полной информации о структуре и параметрах объекта, т. е. о всех его характеристиках.
Преобразуем передаточную функцию (8.1) к полюсно - нулевому представлению в форме Боде
| (8.2) |
где k – коэффициент усиления k = b0/a0 , а ![]() ,
, ![]() – соответственно нули и полюсы передаточной функции.
– соответственно нули и полюсы передаточной функции.
Если среди корней ![]() ,
, ![]() встречаются комплексно сопряженные пары корней, то разложение (8.2) необходимо дополнить сомножителями следующего типа:
встречаются комплексно сопряженные пары корней, то разложение (8.2) необходимо дополнить сомножителями следующего типа:
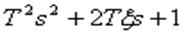 .
.
Предполагая для простоты изложения отсутствие комплексно - сопряженных корней, можно преобразовать (8.2) к следующему виду:
| (8.3) |
где
|
По выражению передаточной функции в форме (8.3) получим частотную передаточную функцию объекта:
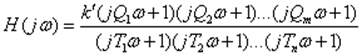 ,
,
Что позволяет получить характерные функции:
ЛАЧХ:
| (8.4) |
ЛФЧХ:
| (8.5) |
С другой стороны, известно, что ЛАЧХ и ЛФЧХ динамических звеньев с передаточными функциями вида:
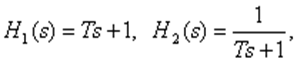
имеют вид, показанный на рис. 8.6, так как звенья являются соответственно форсирующими и апериодическими динамическими звеньями первого порядка.
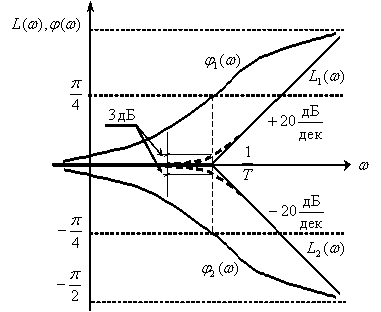
Рис. 8.6
Исходя из изложенного материала, можно предложить следующую процедуру активной идентификации структуры и параметров линейной системы с одним входом и одним выходом:
В процессе эксперимента с объекта снимается частотная характеристика в виде ЛАЧХ и ЛФЧХ.
Полученная экспериментально ЛАЧХ аппроксимируется кусочно-линейной кривой – набором отрезков (асимптот) с целочисленным наклоном кратным 20 дБ / дек
По наклону асимптот и частотам сопряжения асимптот определяется передаточная функция объекта в виде произведения передаточных функций соответствующих асимптотам элементарных динамических звеньев (апериодических и форсирующих).
При наличии в полученной ЛАЧХ и ЛФЧХ признаков звеньев второго порядка, то есть асимптот с наклоном кратным 40 дБ / дек, необходимо ввести такие звенья в модель, например, колебательное звено.
Колебательное звено с передаточной функцией
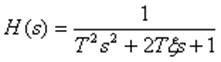
имеет ЛАЧХ и ЛФЧХ, показанные на рис. 8.7.
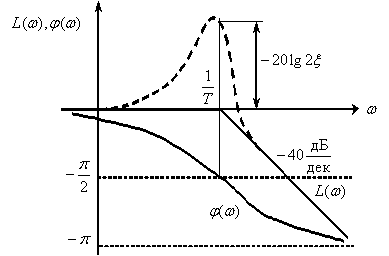
Рис. 8.7
Форсирующее звено второго порядка с передаточной функцией
![]() ,
,
имеет ЛАЧХ (ЛФЧХ) симметричные показанным на рис. 8.7 характеристикам колебательного звена относительно оси частот.
Пример. По экспериментально полученной ЛАЧХ объекта определить его передаточную функцию.
Решение. Аппроксимируем экспериментальную ЛАЧХ набором асимптот, как это показано на рис. 8.8.
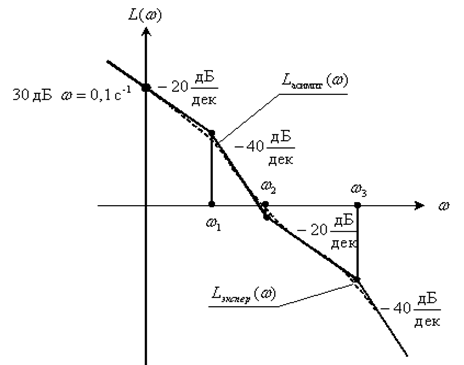
Рис. 8.8
Рассмотрим теперь участки аппроксимированной ЛАЧХ, на которых наклон не изменяется:
![]() .
.
На этом интервале по виду асимптоты ЛАЧХ соответствует ЛАЧХ идеального интегрирующего звена с передаточной функцией вида:
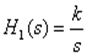 .
.
Этому звену соответствует следующее выражение логарифмической амплитудной характеристики:
![]() .
.
Используем последнее выражение для определения k, подставим значение характеристики при частоте w = 0.1:
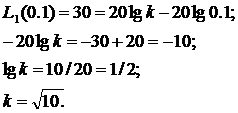
Рассмотрим интервал частот:
![]() .
.
На этом интервале частот наклон асимптоты возрос на 20 дБ/дек и составил 40 дБ/дек, что соответствует добавлению апериодического звена первого порядка с передаточной функцией :
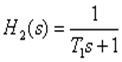
где постоянная времени определяется по точке сопряжения асимптот:
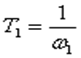
Рассмотрим интервал частот:
![]() .
.
На этом интервале наклон асимптоты уменьшился на 20 дБ/дек, что соответствует добавлению форсирующего звена первого порядка с передаточной функцией:
![]()
где постоянная времени определяется по точке сопряжения асимптот:
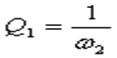 .
.
Рассмотрим интервал частот:
![]() .
.
На этом интервале наклон асимптоты возрос на 20 дБ/дек, что соответствует добавлению апериодического звена первого порядка с передаточной функцией –
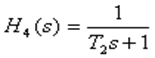 ,
,
где постоянная времени определяется по точке сопряжения асимптот –
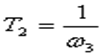 .
.
Перемножая полученные передаточные функции, получим передаточную функцию объекта:
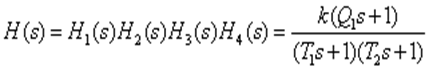
Что и требовалось найти.
9. Задачи детерминированного линейного оптимального управления
9.1. Теоретические сведения
Рассмотрим объект управления, возмущенное движение которого описывается в первом приближении уравнением [5]
| (9.1) |
Здесь А и В – заданные матрицы чисел размеров n×n и n×m соответственно; x(t) – вектор состояния, вектор фазовых координат размерности n×1; u(t) – вектор управления размерности m×1.
Рассмотрим также критерий качества управления:
| (9.2) |
где R1 и R2 – положительно определенные симметрические матрицы размеров n×n и m×m соответственно. Тогда задача определения
u(t), t0 ≤ t ≤ ∞ ,
при котором критерий минимален, называется задачей детерминированного линейного оптимального управления для регулятора с постоянными параметрами.
Закон управления определяется соотношением:
| (9.3) |
где
| (9.4) |
Установившееся решение Р является решением алгебраического уравнения Риккати:
| (9.5) |
Р является неотрицательно определенной матрицей.
9.2. Решение задач управления с применением уравнения Риккати
Задача 9.1. Задача стабилизации угловой скорости.
Объект состоит из двигателя постоянного тока, управляемого входным напряжением μ(t) с угловой скоростью вала ξ(t). Система описывается скалярным дифференциальным уравнением состояния
| (9.6) |
Критерий оптимальности имеет вид:
| (9.7) |
В обозначениях (9.1) – (9.5) имеем
x(t) = ξ(t); u(t) = μ(t) ; A = -α; B =![]() ; R1 = 1; R2 = ρ. (9.8)
; R1 = 1; R2 = ρ. (9.8)
Подставляя (9.8) в (9.5), получим:
| (9.9) |
Из (9.9) определим Р. Будем иметь:
| (9.10) |
Определим матрицу F из (9.4). Получим:
| (9.11) |
или
| (9.12) |
Таким образом,
μ(t) = −Fξ(t). (9.13)
Подставим (9.13), (9.12) в (9.6). Будем иметь:
|
или

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 |