(а)   (б)

(в)

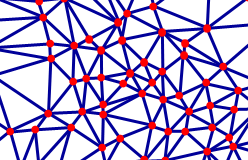
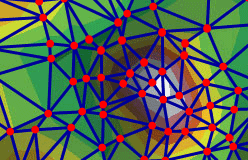
Рис. 5.26. Трехмерное отображение триангуляционной модели рельефа
(а – триангуляция; б – триангуляционная модель рельефа;
в – трехмерное отображение рельефа)

   (а)  (б)

Рис. 5.27. Трехмерное отображение регулярной модели рельефа
(а – регулярная сеть; б –трехмерное отображение рельефа)

3. Векторные данные, которые путем выдавливания по вертикали приобретают объемный вид. Например, слой зданий, представленный в виде полигонов, путём выдавливания вверх на некоторую высоту (в зависимости от значений атрибутов) приобретает вид многогранников. Стороны этих зданий могут быть окрашены одним цветом, либо на них можно нанести текстуру (рис. 5.28).

4. Подписи объектов. Трехмерные подписи бывают двух видов: плоские и трехмерные. Плоские подписи рисуются поверх готового трехмерного изображения вблизи интересующих объектов. При этом недостатком является то, что такие плоские подписи могут взаимно перекрываться, не давая читать текст, и не всегда ясно, к какому объекту относится надпись.

Рис. 5.28. Трехмерное изображение местности с натянутым
на рельеф аэрофотоснимком и векторными данными (здания)

Трехмерные подписи – это, по сути, полноценными трехмерными объектами, являющимися частью трехмерной сцены. Трехмерные подписи обычно подобны дорожным знакам, установленным в некоторых точках местности, но при этом они могут поворачиваться к зрителю. При необходимости можно приблизиться к этой подписи и рассмотреть её.

5. Трехмерные объекты специального назначения. Обычно эти объекты импортируются из других программ в виде готовых трехмерных моделей, представленных в некотором стандартном формате, при этом наиболее часто используются форматы 3D Studio (*.3ds) и X-файлы (*.x). Таким способом можно, например, импортировать детальную 3-мерную модель здания и установить её в некотором месте на карте, при этом здание появится в окне трехмерного вида.

Некоторые геоинформационные системы предоставляют возможности по автоматическому созданию трехмерных моделей некоторых стандартных видов объектов, включая здания (имеющие крыши со скатами), автомобили, самолёты, трубопроводы, дорожные знаки, ограждения, заборы, зеленые насаждения и пр. (рис. 5.29).

В настоящее время наиболее часто используются следующие способы просмотра виртуальных моделей местности:

1. Статический просмотр ВММ с определенной точки зрения. Данный способ наиболее прост и не требует больших мощностей компьютера.

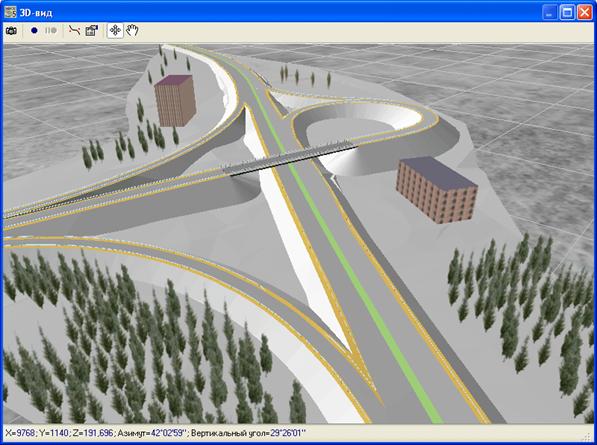
Рис. 5.29. Трехмерное изображение местности с дорогой, зданиями,
путепроводом и зелеными насаждениями

2. Облет ВММ в реальном времени (в режиме самолёта). Этот способ позволяет наиболее полно визуально осмотреть местность, однако он требует высокой мощности видеокарты и компьютера в целом, т. к. для обеспечения эффекта присутствия изображение должно пересчитываться в реальном времени со скоростью не менее 10–20 кадров в секунду. В этом режиме пользователь может передвигаться по трехмерной сцене, используя клавиатуру или мышь.

3. Объезд ВММ в реальном времени (в режиме автомобиля или пешехода). Данный способ, по сути, эквивалентен предыдущему, за исключением того, что в этом случае высота точки зрения над поверхностью фиксирована.

4. Заранее записанный видеофайл. Предыдущие два способа не всегда можно полноценно использовать из-за высоких требований к скорости работы видеокарты и компьютера в целом. Именно поэтому во многих трехмерных ГИС существует возможность создания видеоролика, показывающего изображение вдоль некоторой заранее заданной траектории полёта. ГИС просчитывает отдельные кадры изображения и сохраняет их в видеофайл, например, в формате AVI. После этого полученный видеоролик можно просматривать уже любыми средствами просмотра видеофильмов на обычных (не самых мощных) компьютерах.

Отметим, что большинство ГИС не позволяют работать с реальными большими ВММ в реальном режиме времени. Это обычно связано с техническими особенностями реализации ГИС, когда ВММ целиком загружается в оперативную и видеопамять.

В настоящее время средства работы с ВММ имеются во многих ГИС, однако их большинство имеют существенные ограничения. Среди множества решений для работы с ВММ можно отметить программный продукт SiteBuilder 3D (производитель MultiGen-Paradigm, США), с помощью которого можно создавать виртуальные модели местности с огромным количеством объектов и высокой степенью детализации. Этот продукт реализован как программная надстройка для ArcView GIS 3.2 и для ArcGIS 8.x/9.x.

SiteBuilder 3D по обычным (плоским) данным в ГИС самостоятельно создаёт необходимую ВММ с дополнительными структурами данных, позволяющими выполнять визуализацию трехмерных карт в реальном режиме времени.  На рис. 5.30 приведён пример ВММ, построенного с помощью SiteBuilder 3D на основе карты в ArcView GIS 3.2. В левой части экрана показана исходная двумерная карта, в правой части – соответствующее трехмерное изображение. Для удобства навигации в пространстве в левой части экрана двумя линиями показывается угол обзора.

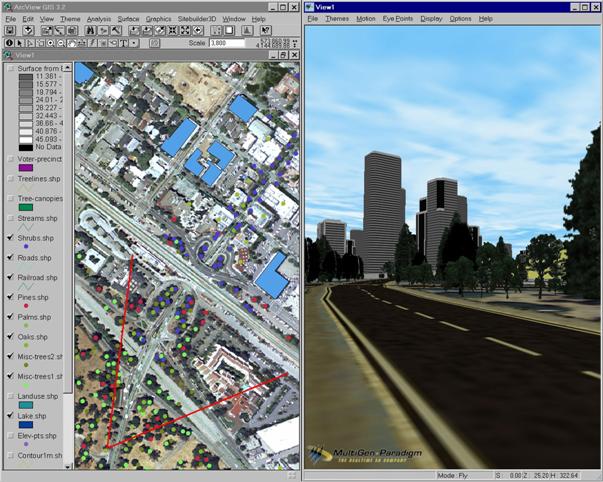
Рис. 5.30. Трехмерное изображение местности, построенное с помощью
программы SiteBuilder 3D в среде ArcView GIS 3.2

5.8. Картографические анимации

Карты в ГИС являются прямым компьютерным аналогом бумажным карт, однако компьютеры также позволяют использовать новые изобразительные возможности, не имеющие аналогов в традиционной картографии. Одним из таких инструментов является функция трехмерной визуализации, рассмотренная в предыдущем разделе. В данном разделе мы рассмотрим другой инструмент, позволяющий создавать динамические (двигающиеся, анимированные) изображения картографических объектов.

Динамические карты можно разделить на следующие виды:

1. Оперативные карты, меняющиеся в соответствии с изменением геометрических или атрибутивных характеристик пространственных объектов. Такие изображения обычно предназначены для оперативного мониторинга состояния объектов в реальном режиме времени.

Типичным применением оперативных карт является отслеживание положения объектов, движущихся на местности. Это могут быть, например, автомобили оперативных служб, перемещающиеся по городу. Эти машины должны быть снабжены GPS-приемниками и периодически передавать информацию в некоторый компьютерный центр с уведомлением об изменении своего положения в пространстве. В этом центре информация о положении автомобилей должна сохраняться в базу данных. В свою очередь, ГИС должна периодически делать запросы к этой базе данных, извлекать оттуда информацию о положении автомобилей и перерисовывать карту с автомобилями (рис. 5.31).

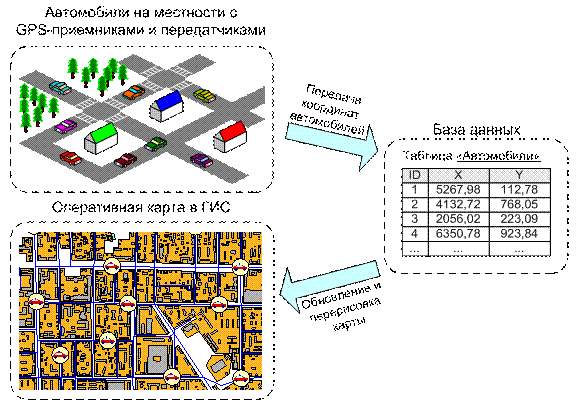
Рис. 5.31. Схема работы системы, отслеживающей с помощью ГИС
положение автомобилей на местности

Ещё одним типичным применением оперативных карт является их использование для отображения различной технологической информации, поступающей с разнообразных датчиков с помощью телеметрии. Например, система управления светофорами в городе состоит из электронной карты, на которой отображается состояние всех светофоров, а также средств удаленного управления светофорами.

Светофоры могут как управляться из единого центра, так и самостоятельно изменять своё состояние (например, по нажатию кнопки пешеходом, желающим перейти дорогу). Поэтому на светофорах должны стоять датчики, передающие в центральную базу данных своё состояние. В свою очередь, ГИС должна периодические опрашивать состояние всех светофоров и перерисовывать изображение карты.

Отметим, что такие системы, включающие средства для отображения и изменения состояния объектов, часто относят к классу программных продуктов АСУ ТП (автоматизированные системы управления технологией производства). Эти АСУ ТП, как правило, включают в себя средства для визуального отображения различных параметров объектов на схемах, чертежах, планах. В ряде случаев АСУ ТП могут быть построены на основе ГИС.

Заметим, что в отличие от предыдущего примера с автомобилями, где менялись геометрические характеристики пространственных объектов (координаты автомобилей на местности), в АСУ ТП геометрия объектов обычно фиксирована, но меняются атрибутивные характеристики. С помощью телеметрии в АСУ ТП снимаются показания с различных приборов и передаются на сервер в базу данных. В свою очередь, ГИС периодически извлекает из базы данных различные атрибуты пространственных объектов и перерисовывает карту (рис. 5.32).

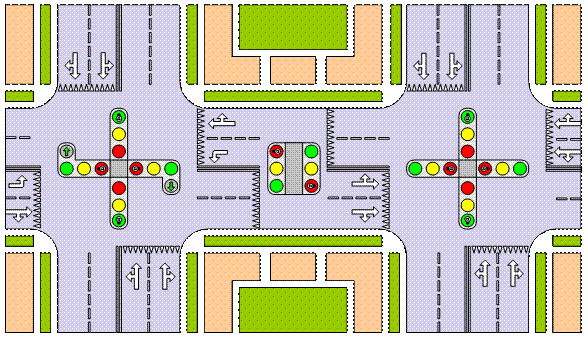
Рис. 5.32. Пример карты, на которой оперативно
отображаются состояния светофоров

2. Карты с анимированными условными знаками. В таких картах используются особые условные знаки, которые постоянно меняют свой внешний вид. В обычной картографии условные знаки характеризуются формой, размером, цветом, яркостью, ориентацией и внутренней структурой. В анимированных условных знаках эти характеристики постоянно меняются по некоторому закону. При этом дополнительной характеристикой условных знаков становится закон изменения знаков, в т. ч. скорость изменения. Рассмотрим некоторые основные способы анимации условных знаков:

Анимация формы. Например, на карте страны города могут быть показаны в виде пульсирующих кружочков. Размер кружочков должен периодически меняться между максимальным размером, пропорциональным населению города, и минимальным (например, составляющим половину от максимального). При этом скорость изменения размера кружочков должна быть пропорциональна среднегодовому приросту населения в процентах. Если прирост населения является отрицательным, то кружочки должны уменьшаться от максимального до минимального размера и затем сразу становится максимальными. Если прирост населения положительный, то кружочки должны увеличиваться.

Анимация цвета. В этом способе цвет условного знака периодически меняется от одного значения до другого, при этом скорость пульсации цвета может быть пропорциональна некоторому заданному параметру.

Анимация положения знака. В этом способе сам условный знак не меняется, но меняется его расположение на карте. Условный знак может перемещаться по некоторым траекториям (например, вдоль преобладающий направлений перемещения воздушных масс), либо выполнять случайные перемещения около одного места. Например, такими условными знаками, размещенные на карте у населенных пунктов, можно описать уровень миграции. При этом частота случайных колебаний условного знака должна быть пропорциональна объему миграции на душу населения, а амплитуда – средней дальности.

3. Анимированные двумерные карты динамики. Такие карты состоят из последовательности карт, содержащий один и тот же набор пространственных объектов (точечных, линейных или площадных), но с разными геометрическими (отражение динамики положения) и атрибутивными (отражение динамики состояния) характеристиками. Таким способом, например, можно показать во времени динамику движения фронтов воздушных масс по поверхности Земли, динамику изменения загрязнений окружающей среды.

Такие карты динамики можно просматривать по отдельным кадрам, выбирая определенную дату и время, либо с помощью ГИС можно заранее просчитать все кадры изображения и сохранить их в видеофайл (типа AVI). Такой файл в дальнейшем можно просматривать любой стандартной программой проигрывания видеофильмов.

4. Анимированные анаморфозы. Данный вид анимации можно рассматривать как разновидность предыдущего вида – карт динамики, показывающих анаморфическими средствами изменение различных параметров во времени. Например, так можно создать видеофильм, показывающий изменение населения Земли в различных регионах во времени.

5. Анимированные двумерные карты движения. В таких картах все объекты являются фиксированными и не меняются во время анимации. Меняется только точка зрения на карту (масштаб изображения и координаты центра карты на экране). Последовательность кадров, соответствующих различным точкам зрения, сохраняется с помощью ГИС в видеофайл для дальнейшего просмотра. Такие анимированные карты движения обычно используются в презентационных целях.

6. Анимированные трехмерные карты динамики. Такие карты, как и в двумерном случае, позволяют анимировать фиксированный набор пространственных объектов, меняющих свои геометрические или атрибутивные характеристики. Основное преимущество трехмерной анимации перед двумерной заключается в более полноценной возможности анимировать поверхности и другие трехмерные объекты.

7. Анимированные трехмерные карты движения. По сути, этот способ анимации рассмотрен в предыдущем разделе, где описаны функции облёта и объезда трехмерной модели местности.

5.9. Вопросы для самопроверки

1. Что такое тематическая карта в ГИС?

2. Какие виды условных знаков бывают в картографии и какими способами они создаются в ГИС?

3. Какие есть в ГИС способы визуализации векторных данных?

4. Какие есть в ГИС способы визуализации растровых данных?

5. Какие есть в ГИС способы визуализации транспортных сетей?

6. Какие есть в ГИС способы визуализации поверхностей?

7. Какие есть в ГИС способы трехмерной визуализации?

8. Что такое картографическая анимация, каково её назначение? Какие виды анимации бывают в ГИС?

Глава 6. Пространственный анализ

6.1. Измерительные операции

К измерительным операциям (картометрическим функциям) в ГИС относят функции, позволяющие определить различные геометрические характеристики объектов, явлений или пространства по карте (в проекции или по поверхности), такие как расстояния, площади, азимуты и др.

Все измерения в ГИС можно обычно выполнять двумя способами: а) указывая объекты, характеристики которых следует получить, и б) интерактивно задавая точки измеряемой геометрической фигуры.

Рассмотрим основные измерительные операции, которые можно выполнять в геоинформационных системах:

1. Определение координат точки на карте. Чтобы воспользоваться этой функцией в большинстве ГИС обычно не требуется переключаться в какой-то специальный режим работы. При перемещении мышки по карте, в строке статуса обычно показываются координаты указанной курсором точки. При этом в строке статуса может отображаться и высотная отметка этой точки, если в ГИС некоторая поверхность выбрана в качестве текущей (рис. 6.1).

Координаты точек, отображаемые в ГИС, обычно показываются в исходных координатах объектов на карте (например, в градусах), однако возможно и в системе координат проекции (например, в метрах в проекции Гаусса-Крюгера).

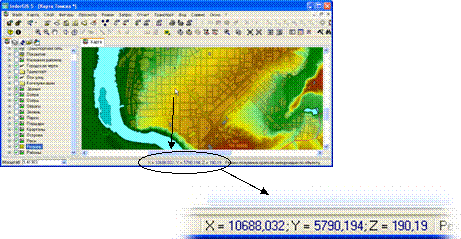
Рис. 6.1. Определение координат точек на местности

2. Измерение расстояний, азимутов и углов. Пользователь должен указать на карте в ГИС последовательность точек ломаной, длину которой надо вычислить. ГИС выводит в строке статуса общую длину ломаной, а также длину последнего сегмента ломаной. Кроме того, для последнего сегмента может выводиться азимут и угол поворота относительно предыдущего сегмента (рис. 6.2).

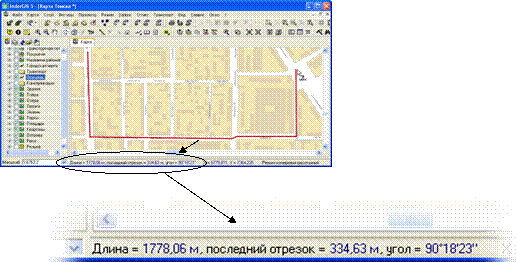
Рис. 6.2. Измерение расстояний

3. Измерение площадей и периметров. Как и в предыдущем способе, пользователь должен задать в ГИС вершины некоторого многоугольника. При этом в строке статуса ГИС будет выводиться площадь и периметр (рис. 6.3).

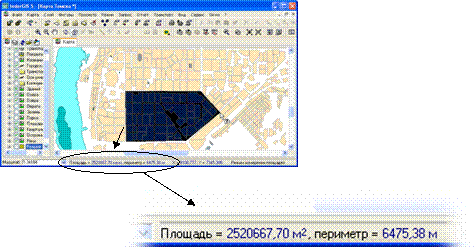
Рис. 6.3. Измерения площадей

5. Измерение линейных координат (пикета и смещения) точки относительно трассы. В этом режиме пользователь должен указать некоторую линию, относительно которой производится определение линейных координат. Далее, перемещая курсор мышки по карте, в строке статуса ГИС будет выводиться пикет и смещение указанной точки (рис. 6.4).

В заключение отметим, что некоторые геоинформационные системы предоставляют возможности по измерению расстояний и площадей с учетом формы земной поверхности. При этом вычисления могут происходить либо по поверхности референц-эллипсоида, либо по некоторой цифровой модели рельефа, заданной в виде регулярной или нерегулярной сети.

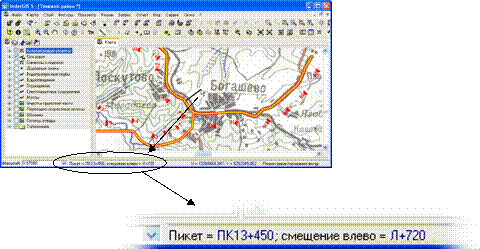
Рис. 6.4. Измерения линейных координат (определение пикета и смещения)

6.2. Векторный анализ

Под термином векторный анализ в геоинформатике подразумевается набор инструментов, позволяющих анализировать существующие геометрических объектов и строить новые.

Все операции векторного анализа определены над фигурами трёх типов: точечными, линейными и площадными.

В следующих подразделах мы рассмотрим различные виды операций векторного анализа и их применение на практике.

6.2.1. Анализ отношений

При анализе пространственных объектов часто возникают задачи поиска объектов, касающиеся друг друга, являющиеся смежными, вложенными, или состоящими в каких-то иных отношениях.  Например, пусть задана некоторая автомобильная дорога на карте области. По карте земельных участков мы можем определить полосу отвода, в которой находится дорога, и соответствующую охранную зону. Далее мы можем найти все здания, попадающие внутрь соответствующей охранной зоны.

Все операции анализа отношений делятся на три группы:

А). Бинарные операции выявления отношений между парой заданных объектов. Результатом таких операций является логическое значение, определяющее, находятся ли два объекта в этом отношении или нет.

Б). Поисковые запросы, извлекающие все объекты из заданного набора пространственных данных, находящиеся в некотором бинарном отношении с указанным объектом. Результатом этой операции является множество объектов из заданного набора данных, удовлетворяющих указанному соотношению.

В). Операции пространственного соединения двух наборов пространственных данных. Результатом этой операции является множество пар объектов, удовлетворяющих некоторому заданному бинарному отношению, причем первые объекты в этих парах должны принадлежать первому набору пространственных данных, а вторые объект – второму.

Всего выделяют 8 основных видов бинарных отношений между пространственными объектами. Далее мы их рассмотрим, а для каждого из них будут приведем рисунки, комментирующие их для 3 основных типов (в зависимости от размерности) векторных данных: точечных (0-мерных), линейных (1-мерных) и площадных (2-мерных). Для некоторых сочетаний типов фигур описываемые операции не имеют смысла, о чем указывается на рисунках.

Каждое рассматриваемое отношение имеет два аргумента, которые на рисунке обозначены как «Первая фигура» и «Вторая фигура», соответственно, на пересечении размещается пример отношения. Все отношения имеют названия в форме глагола (возможно с последующим предлогом), например, «Содержит в себе», поэтому отношение следует читать по следующему шаблону: «Первая фигура содержит в себе вторую фигуру».

Итак, рассмотрим эти отношения:

1. Отношение «Совпадает с» (Equals). Две фигуры находятся в этом отношении, если они совпадают между собой (рис. 6.5). При этом фигуры считаются совпадающими, если все узловые точки фигур (ломаных или полигонов) имеют совпадающие координаты. Отношение определено только для фигур, имеющих одинаковую размерность.

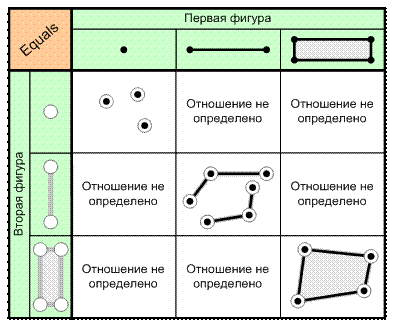
Рис. 6.5. Отношение «Совпадает с» (Equals)

2. Отношение «Содержит в себе» (Contains). Две фигуры находятся в этом отношении, если вторая фигура находится внутри первой, при этом ни одна точка второй фигуры не должна находиться вне первой (рис. 6.6). Отношение не определено в случае, когда вторая фигур имеет большую размерность, чем первая.

Вариантом этого отношения является «Полностью содержит в себе» (Covers) , когда вторая фигура не может пересекать границу первой.

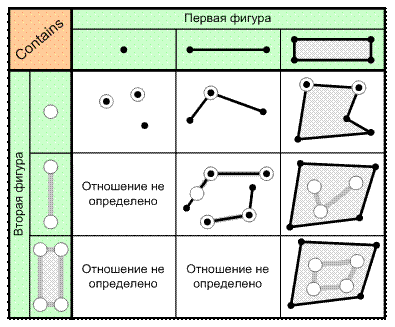
Рис. 6.6. Отношение «Содержит в себе» (Contains)

3. Отношение «Содержится в» (Within, Inside). Две фигуры находятся в этом отношении, если первая фигура находится внутри второй, при этом ни одна точка первой фигуры не должна находиться вне второй (рис. 6.7). Отношение не определено в случае, когда вторая фигур имеет меньшую размерность, чем первая. По сути, это отношение является обратным по отношению к предыдущему («Содержит в себе»), т. е. надо только поменять местами аргументы отношения.

Вариантом этого отношения является «Полностью содержится в» (Covered By), когда первая фигура не может пересекать границу второй.

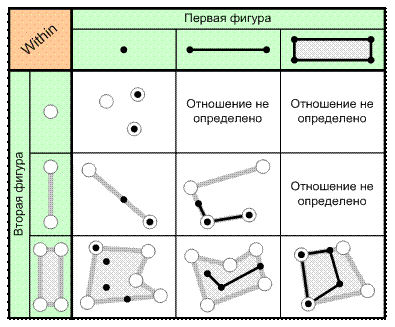
Рис. 6.7. Отношение «Содержится в» (Within)

4. Отношение «Пересекается с» (Crosses). Отношение определено только между линейными и площадными объектами, при этом хотя бы одна фигура должна быть линией. Если обе фигуры являются площадными, то такое отношение называется «Накладывается на» и рассматривается ниже. Две фигуры находятся в этом отношении, если эти фигуры имеют общие точки, т. е. две линии должны иметь точку пересечения, а линия и полигон должны пересекаться по некоторой линии (рис. 6.8).

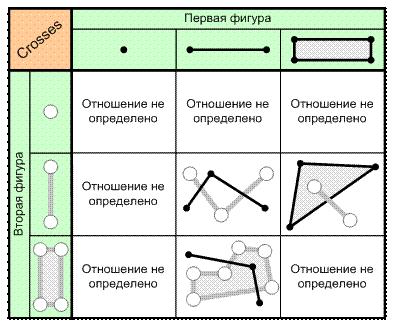
Рис. 6.8. Отношение «Пересекается с» (Crosses)

5. Отношение «Отделена от» (Disjoint). Две фигуры находятся в этом отношении, если обе фигуры не имеют общих точек (рис. 6.9).

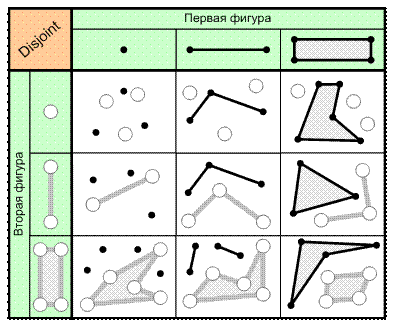
Рис. 6.9. Отношение «Отделена от» (Disjoint)

6. Отношение «Перекрывается с» (Overlaps). Две фигуры находятся в этом отношении, если область пересечения этих фигур имеет ту же размерность, что и сами фигуры, т. е. эти фигуры имеют общие внутренние точки (рис. 6.10). Отношение определено только для фигур, имеющих одинаковую размерность.

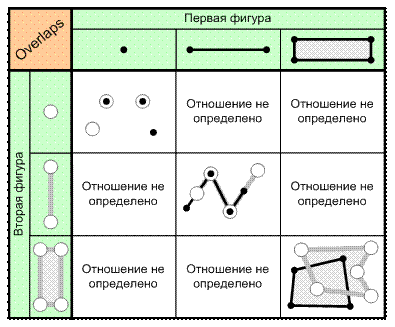
Рис. 6.10. Отношение «Перекрывается с» (Overlaps)

7. Отношение «Граничит с» (Touches). Две фигуры находятся в этом отношении, если эти фигуры соприкасаются только своими границами, но не своими внутренними областями, т. е. ломаные могут касаться только своими вершинами, а полигоны – своими контурами (рис. 6.11). Отношение не определено только для двух точечных фигур.

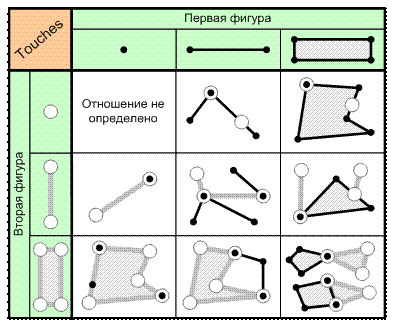
Рис. 6.11. Отношение «Граничит с» (Touches)

8. Отношение «Касается» (Any Interacts). Две фигуры находятся в этом отношении, если эти фигуры имеют общие точки (рис. 6.12).

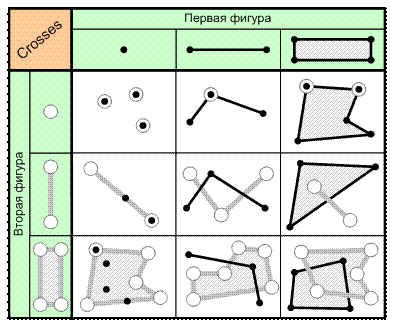
Рис. 6.12. Отношение «Касается» (Any Interacts)

Помимо бинарных отношений, существуют и иные отношения, например, такое тернарное (аргументами в котором являются две фигуры и некоторый параметр) как «На расстоянии» (Distance). В различных вариантах этого отношения требуется, чтобы расстояние между ближайшими точками двух фигур было равно, менее, более, не более или не менее заданной величины.

Как было сказано выше, в поисковых запросах из заданного набора данных извлекаются все фигуры, находящиеся в некотором бинарном отношении с указанной фигурой. Однако наиболее часто на практике используются следующие виды запросов (особенно при интерактивном выделении объектов на карте):

1. Поиск фигур, вложенных в заданный прямоугольник, круг или произвольный многоугольник. Найденные объекты должны целиком помещаться внутри заданной фигуры.

2. Поиск фигур, пересекающихся с заданным прямоугольником, кругом или произвольным многоугольником. Найденные фигуры должны полностью или хотя бы частично помещаться внутри заданной фигуры.

Также отметим, что среди всех возможных операций соединения наиболее часто используются следующие:

1. Поиск всех пар вложенных многоугольников среди двух множеств многоугольников, когда многоугольник из первого множеств должен войти в многоугольник из второго множества.

2. Поиск всех пар пересекающихся многоугольников среди двух множеств многоугольников, когда многоугольник из первого множеств должен пересечься с некоторым многоугольником из второго множества.

В заключение отметим, что проверки отношений фигур всегда выполняются с некоторой заданной величиной допуска, при этом точки, координаты которых отличаются на величину, меньшую заданного допуска, считаются совпадающими.

6.2.2. Отсечение и разрезание

Операция отсечения позволяет удалить части пространственного объекта, лежащие вне области отсечения. При этом части, лежащие на границе области отсечения, считаются попадающими внутрь области, а потому не отсекаются. В качестве области отсечения может выступать любой площадной объект, но обычно используются прямоугольники и одноконтурные многоугольники, реже – произвольные многоконтурные многоугольники и круги.

Операция отсечения может быть применена для пространственных объектов любой размерности. Если исходный объект целиком содержится в области отсечения, то операция возвращает исходный объект без изменений. Иначе, отсекая некоторые части исходного, создаётся новый пространственный объект, который целиком содержится в области отсечения. При этом из-за отсечения от объекта может вообще ничего не остаться, и поэтому операция отсечения не возвратит пустой объект. Если новый объект будет иметь меньшую размерность, чем исходный, то операция отсечения также ничего не возвратит. Иначе операция отсечения возвратит новый объект, имеющий ту же размерность, что и исходный объект.

На рис. 6.13 приведён пример выполнения операции отсечения для фигур различного вида. В качестве примера 0-мерных (точечных) объектов используется мультиточка – фигура, состоящая из нескольких точек.

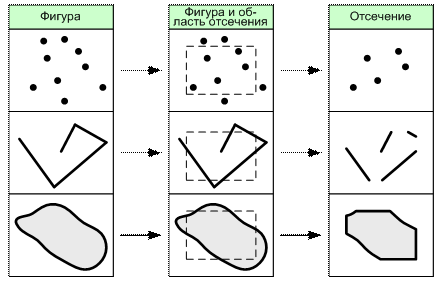
Рис. 6.13. Операция отсечения пространственных объектов

В ГИС операция отсечения обычно реализована следующим образом. Пользователь выделяет некоторые объекты на карте и выбирает команду отсечения. Затем ГИС предлагает пользователю интерактивно указать на карте область отсечения (прямоугольник, многоугольник, окружность), после чего у выделенных фигур ГИС отсекает части, лежащие вне заданной области.

Операция разрезания во многом похожа на отсечение. Эта операция позволяет разрезать некоторый линейный или площадной объект вдоль заданной ломаной, которая не должна самопересекаться. Результатом операции разрезания являются отрезы слева и справа – части исходного объекта, оказавшиеся по разные стороны от линии разреза (рис. 6.14).

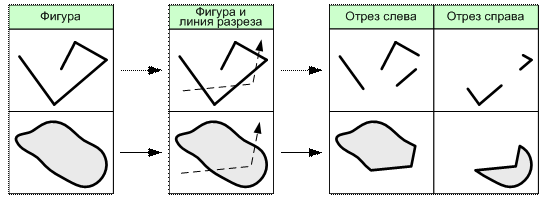
Рис. 6.14. Операция разрезания пространственных объектов

В ГИС операция разрезания обычно реализована следующим образом. Пользователь выделяет некоторые объекты на карте и выбирает команду отсечения. Затем ГИС предлагает пользователю интерактивно указать на карте ломаную разрезания, после чего выделенные фигуры ГИС разрезает на части, лежащие слева и справа от заданной ломаной.

6.2.3. Оверлейные операции

Оверлейные операции (операции наложения, картографической алгебры, алгебры карт) позволяют вычислять объединения, пересечения или разности отдельных пространственных объектов или сразу двух множеств объектов. Оверлейные операции определены для пространственных объектов всех размерностей, но в одной операции могут участвовать только объекты одной размерности. Результатом операции является новый объект, имеющий ту же размерность, что и исходные объекты, либо пустое множество. Иногда в результате формального выполнения правил оверлейных операций могут возникать фигуры меньшей размерности (например, область пересечения двух граничащих фигур является линией или точкой), чем исходные, но такие фигуры отбрасываются, и считается, что операция возвращает пустое множество.

Результатом операции объединения двух пространственных объектов является объект, состоящий из всех точек плоскости, которые принадлежат хотя бы одному исходному объекту (рис. 6.15).

Результатом операции пересечения двух пространственных объектов является объект, состоящий из всех точек плоскости, которые принадлежат обоим исходным объектам (рис. 6.16).

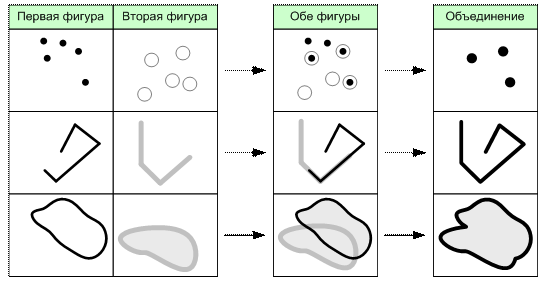
Рис. 6.15. Операция объединения пространственных объектов

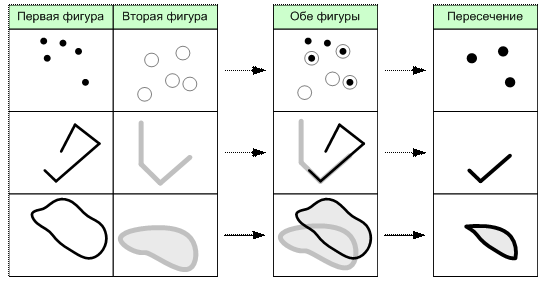
Рис. 6.16. Операция пересечения пространственных объектов

Результатом операции разности двух пространственных объектов является объект, состоящий из всех точек плоскости, которые принадлежат первому объекту, но не принадлежит второму (рис. 6.17).

Результатом операции симметрической разности двух объектов является объект, состоящий из всех точек плоскости, которые принадлежат первому или второму объекту, но обоим сразу (рис. 6.18).

Операции построения объединения, пересечения и разности линий и многоугольников имеются во многих графических программах, не являющихся ГИС. Однако в ГИС мы имеем дело не просто с геометрическими фигурами, а пространственными объектами, которые помимо геометрической составляющей ещё имеют атрибуты. Именно поэтому после выполнения оверлеев новые объекты должны иметь атрибуты, значения которых формируются на основе исходных объектов. Новый набор атрибутов обычно является объединением наборов атрибутов исходных объектов. При этом значения новых атрибутов определяются на основании значений исходных атрибутов одним из двух следующих способов:

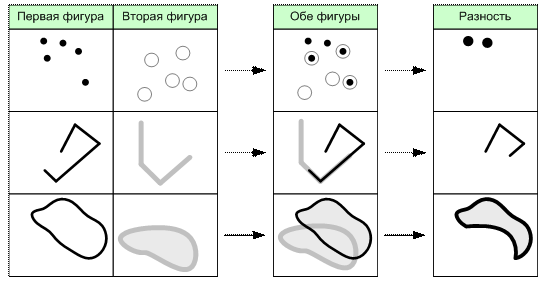
Рис. 6.17. Операция разности пространственных объектов

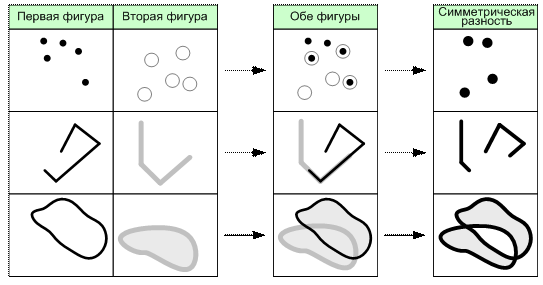
Рис. 6.18. Операция симметрической разности пространственных объектов

1. Значение атрибута просто копируется из исходного объекта. Если этот атрибут был в обоих исходных объектах, то берётся атрибут из того объекта, площадь которого больше. Такой способ используется, если в атрибуте хранятся не числа (строки, дата, время, логические значения) или числа, не имеющие непрерывную интерпретацию (например, код типа земельных угодий).

2. Значение атрибута меняется пропорционально изменению площади нового объекта по отношению к исходному.

6.2.4. Буферные зоны, оболочки, зоны близости

Буферная зона вокруг фигуры F – это наибольшая область на карте, все точки внутри которой удалены от F не более чем на заданное расстояние L (рис. 6.19). При построении в ГИС буферных зон расстояние L может быть задано заранее, либо вычисляться динамически для каждого объекта отдельно на основе его атрибутов. Некоторые ГИС позволяют за раз построить для каждого объекта не одну буферную зону, а сразу несколько кольцевых буферных зон. Например, указав  и что нужно построить по 3 зоны, будут созданы 3 области, в первой из которых расстояние l от любой точки до исходного объекта будет , во второй , а в третьей .

Буферные зоны используются в геоинформатике, например, для моделирования полос отведения вдоль дорог, санитарных зон вокруг рек и озер, охранных зон вдоль линий газопроводов и линий электропередачи, оценки областей неблагоприятного воздействия на человека вокруг различных источников.

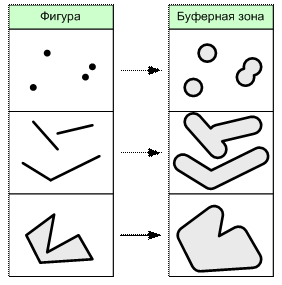
Рис. 6.19. Операция построения буферной зоны

Выпуклая оболочка множества объектов F – это наименьшая выпуклая область на карте, содержащая все объекты F (рис. 6.20). Оболочка может быть построена по объектам любой размерности, но результатом в ГИС всегда является полигон.

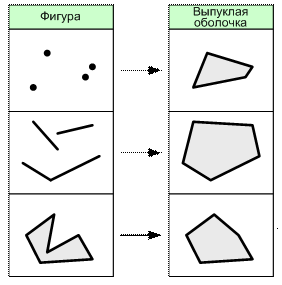
Рис. 6.20. Операция построения выпуклой оболочки

В задаче построения зон близости требуется найти все точки плоскости, для которых расстояние s до заданного множества объектов  является минимальным. В случае, когда все объекты являются точками, данная задача известна как задача построения диаграмм Вороного (рис. 6.21).

Операция построения зон близости может использоваться, например, для нахождения зон скорейшего обслуживания (зон близости) из заданных базовых пунктов. Пусть, например, в некоторых точках на территории региона расположены аэродромы с пожарными вертолётами. В случае возникновения лесного пожара, по заданной точке его локализации мы определяем зону близости, а, следовательно, и вертолёт, который быстрее всех сможет долететь до места пожара.

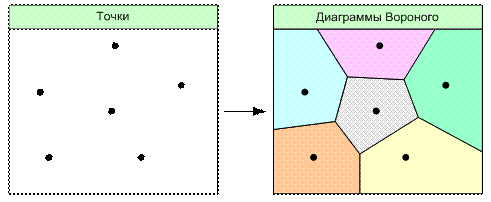
Рис. 6.21. Операция построения диаграмм Вороного
(построение зон близости для точечных объектов)

Приведенный пример предполагает одинаковые скорости перемещения вертолётов, но в действительности они могут отличаться, также могут отличаться и удельные затраты на перемещение.

В операции построения взвешенных зон близости требуется определить все точки плоскости, для которых расстояние s до заданного множества объектов , помноженное на веса , является минимальным.

Для нашего примера укажем скорости полёта вертолётов в качестве весов . Полученные взвешенные зоны близости приведены на рис. 6.22.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20