·  ·  ГИС для ввода и обработки данных. К этой категории относят программы, предназначенные для подготовки исходных данных для ГИС с помощью векторизации и обработки данных дистанционного зондирования.

·  ·  Специализированные ГИС. К этой категории относят ГИС, предназначенные для применения в конкретной отрасли.

5. Виды ГИС по используемой модели данных:

·  ·  Векторные ГИС. Такие системы работают с топологическими и нетопологическими моделями данных, а также иногда с триангуляционными моделями поверхностей.

·  ·  Растровые ГИС. Эти системы позволяют работают только с растровыми моделями данных и иногда с регулярными моделями поверхностей.

·  ·  Гибридные ГИС. Такие системы совмещают в себе возможности векторных и растровых ГИС.

6. Виды ГИС по компьютерной платформе, на которой функционирует ГИС (рис. 1.8):

·  ·  Настольные ГИС. К этой категории относятся большинство известных ГИС. Используемые в их данные как правило сохраняются в файлах, а компьютеры как серверы пространственных данных если и используются, то только в качестве файл-серверов.

·  ·  Клиент-серверные ГИС. В этих системах пространственные данные хранятся полностью в базе данных, обслуживаемой особой программой – сервером пространственных данных. Этот сервер обычно является высокоуровневой надстройкой над некоторой промышленной системой управления базами данных (СУБД типа Microsoft SQL Server, Oracle, DB2, Sybase и др.). Заметим, что многие современные клиент-серверные ГИС могут работать не только с серверами, но также и напрямую с данными в файлах, т. е. эти ГИС также можно отнести к категории настольных.

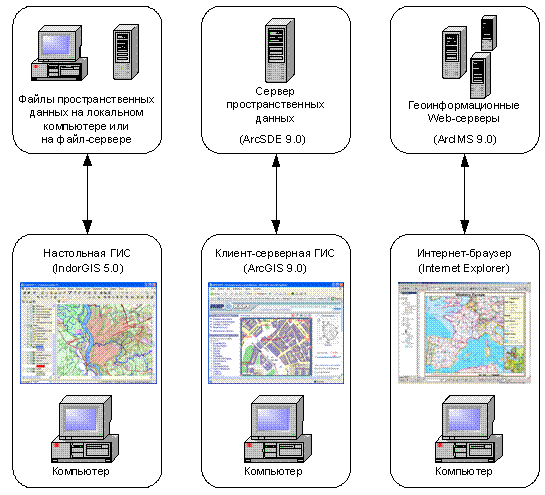
Рис. 1.8. Виды ГИС по компьютерной платформе

·  ·  ГИС для Интернет. Такие системы бывают двух видов: а) самостоятельные программы, обеспечивающее полные функции HTTP-сервера, либо б) наборы программных компонент (обычно ActiveX-объектов), которые могут быть интегрированы в существующий Html-код и произвольным образом настроены. Первый подход позволяет очень быстро выполнить публикацию карт в интернете, но второй подход более гибок.

Следует заметить, что термином ГИС называются очень многие и разные информационные системы. Этим словом описывают как собственно прикладные программы для различных отраслей, так и сами инструментальные ГИС, на основе которых создаются конкретные отраслевые ГИС.

1.5. Организация данных в ГИС

В основе геоинформационных систем лежит концепция послойной организации пространственных данных, когда однотипные данные на земной поверхности группируются в слои (иногда называемые темами). Совокупность всех слоёв в ГИС образует карту.

Деление объектов на слои производится так, чтобы в одном слое а) объекты были одной природы происхождения (дороги, реки, здания), б) объекты желательно имели одинаковую топологическую структуру и размерность (т. е. когда их можно описать точками, линиями или полигонами).

В тоже время, чрезмерно большое количество слоёв создавать нежелательно. Например, нет смысла создавать отдельные слои для автомобилей разных марок, лучше сделать один слой с автомобилями, при этом каждому объекту, описывающему автомобиль, следует сопоставить код марки автомобиля.

В верхней части рис. 1.9 приведен пример городской застройки, на которой изображены жилые дома, фабрики, заправка, склады, различные автомобили, лесопарковая зона, река, улицы, мост, тоннель. Для геоинформационной системы можно было создать 5 основных слоёв:

1. Слой автомобилей. Каждый автомобиль должен представляться в виде точки и дополнительно описываться параметрами цвета и марки.

2. Слой автомобильных дорог. В зависимости от решаемых задач автомобильные дороги могут быть представлены в виде осевых линий, либо в виде многоугольников, точно описывающих проезжую часть. В некоторых случаях имеет смысл иметь два отдельных слоя для осевых линий дорог и для проезжих частей.

3. Слой деревьев. Деревья можно представить в ГИС в виде точечных объектов, для каждого из которых заданы атрибуты типа дерева, высоты, диаметра. Альтернативно крупные лесопарковые массивы могут быть описаны в виде многоугольников, окаймляющих сплошные зоны насаждений. Для каждого такого массива деревьев в атрибутах следует указать плотность посадки, среднюю высоту деревьев.

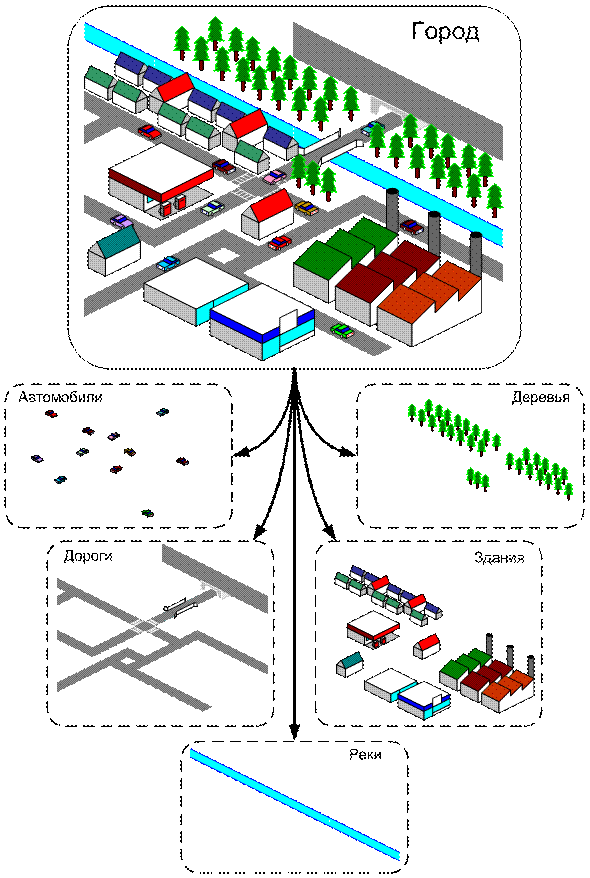
Рис. 1.9. Общая схема деления пространственных данных в ГИС
на отдельные слои – наборы однотипных данных

4. Слой зданий. Здания представляются в виде многоугольников, описывающих контур здания на уровне земли. Для зданий в атрибутах следует указать тип здания (жилое, промышленное, коммерческое), адрес, высоту, количество этажей и др.

5. Слой рек. Реки на карте города обычно представляются в виде многоугольников. На других более мелких картах (картах области или всей страны) реки часто моделируют с помощью ломаных.

Деление данных на слои позволяет работать в ГИС только с теми данными, которые необходимы для решения поставленных задач. В самом простом случае можно «выключить» те слои, которые нам не нужны, и увидеть на карте оставшиеся.

1.6. Вопросы для самопроверки

1. В чем основное отличие ГИС от других информационных систем?

2. Каковы основные функциональные возможности ГИС?

3. Как выглядит типичная ГИС с точки зрения пользователя?

4. Какие критерии используются при классификации ГИС?

5. В каких областях человеческой деятельности целесообразно применять ГИС?

6. Как организованы данные в ГИС?

Глава 2. Модели пространственных данных

2.1. Классификация моделей

В основе геоинформационных систем лежат различные модели данных, являющиеся отражением реальных сущностей на местности, отношений между ними и других дополнительных знаний, имеющих пространственную привязку. Каждая модель данных ГИС включает в себя различные отдельные пространственные объекты, связанные между собой дополнительными топологическими отношениями.

Определение. Пространственный объект (цифровая модель объекта местности) – цифровое представление некоторого объекта реальности, включающее координатную привязку и набор атрибутов (текстовых и числовых характеристик) набор атрибутовъекта местностиреальности, имеющих координатную привязку. и внутренней).

В современных ГИС обычно используются следующие базовые типы пространственных объектов (рис. 2.1):

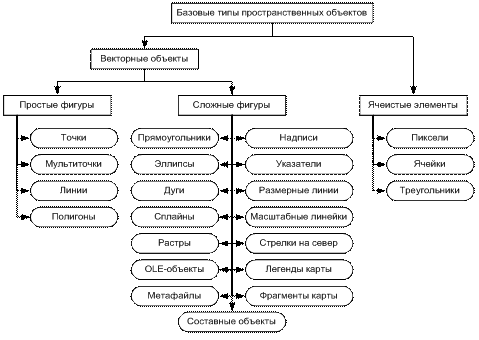
Рис. 2.1. Базовые типы пространственных объектов

Векторные объекты (используются в нетопологической и топологической моделях данных):

1. Точки – 0-мерные (точечные) объекты, характеризуемые координатами на плоскости или в пространстве.

2. Мультиточки – 0-мерные (точечные) объекты, состоящие из нескольких (не менее одной) точек. Этот тип объектов является обобщением типа «Точки».

3. Линии (полилинии, полиполилинии) – 1-мерные (линейные) объекты, состоящие из последовательности (не менее двух) точек, соединённых между собой отрезками (сегментами, дугами). Заметим, что не все последовательные точки могут соединяться между собой отрезками, а потому объекты данного типа могут иметь разрывы, т. е. быть топологически несвязанными. Топологически связанные линии обычно называют полилиниями, а несвязанные – полиполилиниями.

4. Полигоны (области, регионы) – 2-мерные (площадные) объекты, состоящие из нескольких (не менее одного) контуров, заданных в виде последовательности замкнутых линий, и частей плоскости внутри контуров.

Вышеприведенные типы векторных фигур называют простыми в противовес следующим:

5. Сложные фигуры (фигуры оформления, объекты САПР) – разнообразные 0-, 1-, 2- и 3-мерные фигуры, используемые в ГИС для оформления. При этом на практике используются прямоугольники, эллипсы, дуги эллипса, сплайны, внедренные изображения (в виде растров и метафайлов), OLE-объекты, различные текстовые надписи, указатели, размерные линии, а также специальные объекты для оформления карт в ГИС (масштабные линейки, стрелки направления на север, легенды карты, фрагменты других карт).

При выполнении операций пространственного анализа (построение оверлеев, буферных зон, анализ близости) с использованием сложных фигур вначале выполняется их преобразование к простым типам.

Ячеистые элементы (элементы растровых, регулярных и нерегулярных моделей):

6. Пиксели – 2-мерные (площадные) прямоугольные объекты, являющиеся элементами регулярной прямоугольной решетки в растровой модели данных.

7. Ячейки – 2-мерные (площадные) объекты, являющиеся элементами регулярного разбиения в модели регулярной сети.

8. Треугольники – 2-мерные (площадные) объекты, являющиеся элементами разбиения поверхности на треугольники в нерегулярной модели триангуляции.

Определение. Модель данных – способ описания однотипных пространственных объектов, включающий способ описания отдельных объектов, топологических отношений между ними, а также дополнительных знаний о всей совокупности объектов в модели.

Все множество моделей пространственных данных делится на две большие группы (рис. 2.2).

Векторные модели предназначены для описания совокупностей отдельных объектов, например, границ рек, озер, контуров зданий, осей дорог и инженерных коммуникаций. В векторных моделях каждый объект задается некоторым набором координат на плоскости или в пространстве, а также совокупностью атрибутов.

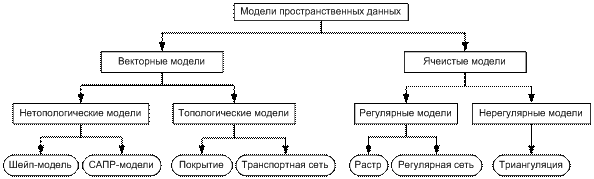
Рис. 2.2. Модели пространственных данных

В векторных нетопологических  моделях все объекты являются полностью независимыми друг от друга и могут произвольно размещаться в пространстве.

Векторные топологические модели состоят из собственно описания отдельных объектов, а также из описаний топологии – отношений отдельных объектов между собой. Наиболее распространенными топологическими моделями являются линейно-узловая модель (покрытие) и транспортная сеть.

Ячеистые модели описывают непрерывные поля данных, такие как фотоснимки местности, поля загрязнений окружающей среды, высотных отметок (рельеф). В ячеистых моделях некоторый участок территории неразрывно разбивается на одинаковые (прямоугольники в растровой или треугольники в регулярной модели) или различные фрагменты (треугольники в нерегулярной триангуляционной модели), каждый из которых описывается своим набором атрибутов.

В геоинформационных системах  все данные организуются в логические группы (тематические), называемые слоями, которые, в свою очередь, группируются в карты.

Определение. Слой карты (тема) – совокупность однотипных пространственных объектов, определенных в одной модели данных на общей территории и в общей системе координат.

Определение. Карта в ГИС – совокупность различных слоёв, определенных на общей территории и в общей системе координат.

В заключение этого раздела рассмотрим еще несколько важнейших понятий.

Определение. Цифровая модель местности (ЦММ) – математическая модель местности, состоящая из множества наборов пространственных данных, описывающих различные виды сущностей и знаний о земле.

ЦММ соответствует объектному составу топографических карт и планов и включает в себя описание формы рельефа земли, природных и антропогенных объектов и сооружений.

Определение. Цифровая карта – математическая модель графического изображения бумажных карт, общепринятых в картографии. В некотором смысле цифровая карта является упрощенным представлением ЦММ, включая в себя только те данные по объектам местности, которые непосредственно отображаются на карте.

Определение. Цифровая модель рельефа (ЦМР) – часть цифровой модели местности, описывающая форму земной поверхности. ЦМР в геоинформационных системах моделируется с помощью ячеистых моделей данных, называемых обычно DEM (регулярная сеть высот) и TIN (нерегулярная триангуляционная сеть).

В геоинформационных системах ЦММ, цифровые карты и ЦМР являются частью соответствующих карт и представляются в виде совокупности слоёв.

2.2. Нетопологическая модель данных

В векторных нетопологических  моделях все объекты произвольно и независимо размещены в пространстве.

Термин «нетопологическая» в противовес «топологической» подчеркивает, что различные фигуры в пределах набора данных никак между собой не связаны и не влияют друг на друга.

Среди векторных нетопологических моделей выделяют два основных подвида: шейп-модель и САПР-модель.

2.2.1. Шейп-модель

В шейп-модели допустимы 4 вида данных: точки, линии, полигоны и мультиточки. При этом в пределах одного слоя карты, представленного в виде шейп-модели, допускаются объекты только одного вида. Соответствующие слои карты при этом называются точечными, линейными, полигональными (площадными) и мультиточечными.

Данные в шейп-модели могут быть определены на плоскости, и тогда они характеризуются двумя координатами , а также в 3-х (координаты  или ) и 4-мерном (координаты ) пространстве. Координата m обычно используется в качестве так называемой «меры» для линий, когда значение меры описывает расстояние от некоторого начала (пикетажное расстояние). Для других типов шейп-данных (точек, полигонов и мультиточек) мера обычно не используется.

1. Точки в шейп-модели являются 0-мерными объектами, описываемыми набором соответствующих координат на плоскости или в пространстве. Точки используются для представления на карте таких объектов, как города на карте мира, колодцы, пожарные гидранты на плане города, высотные отметки рельефа.

2. Мультиточки в шейп-модели также являются 0-мерными объектами и состоят из ненулевого набора несоединённых точек. Этот тип объектов является обобщением типа «точки». Мультиточки используются на практике достаточно редко.

3. Линии в шейп-модели являются 1-мерными (линейными) объектами и определяются как последовательности соединённых отрезками точек. При этом выделяют 3 вида линий: спагетти, струны и кольца.

Спагетти могут самопересекаться, тогда как струны и кольца не могут. Кольца имеют совпадающие начальную и конечную точки. Все линейные объекты имеют некоторое значение длины, но всегда нулевую площадь.

Спагетти должны состоять по крайней мере из одного отрезка, соединяющего две несовпадающие точки. Спагетти обычно используются при экспорте данных из некоторого источника линейных данных, где топологическая корректность данных не гарантируется. На рис. 2.3 приведён пример допустимого объекта типа спагетти.

Рис. 2.3. Пример данных типа «спагетти»

Струны также должны состоять по крайней мере из одного отрезка, соединяющего две несовпадающие точки. При вводе и редактировании струн производится проверка на то, чтобы не было самопересечений отрезков струны, а также последовательных коллинеарных отрезков. На рис. 2.4 приведены примеры допустимой и недопустимой струн.

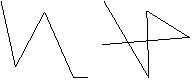
Рис. 2.4. Пример данных типа «струна»

(слева – допустимые, справа – нет)

Кольца должны иметь совпадающие начальную и конечную точки. При вводе и редактировании колец производится проверка на отсутствие самопересечений отрезков кольца, а также последовательных коллинеарных отрезков. На рис. 2.5 приведены примеры допустимого и недопустимого кольца.

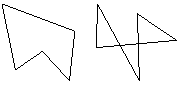
Рис. 2.5. Пример данных типа «кольцо»

(слева – допустимые, справа – нет)

4. Полигоны в шейп-модели являются 2-мерными (площадными) объектами и определяются несколькими (не менее одного) контурами, заданными в виде последовательности замкнутых непересекающихся линий. По крайней мере, один из этих контуров должен быть внешним, а остальные – внутреннми. Внутренние контуры при этом должны задаваться в порядке обхода контура по часовой стрелке, а внешние – против.

На рис. 2.6 приведены пример полигона.

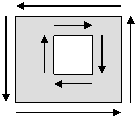
Рис. 2.6. Пример данных типа «полигон»

Для каждой фигуры в шейп-модели данных может храниться некоторое число дополнительных числовых или текстовых параметров (атрибутов), описывающих различные характеристики моделируемых объектов.

2.2.2. САПР-модель

САПР-модель используется в геоинформационных системах как правило для графического оформления карт и для создания сложных чертежей. При этом в пределах одного слоя карты, представленного в САПР-модели, допускаются объекты различных типов: простые (точки, мультиточки, линии, полигоны) и сложные (прямоугольники, дуги, эллипсы, сплайны, растры, метафайлы, OLE-объекты, надписи, указатели, размерные линии и элементы оформления карт).

САПР-модель используется для создания на картографической основе сложных графических изображений, например, схем инженерных сетей.

2.3. Топологическая модель данных

Векторная топологическая модель данных содержит 3 основных типа объектов: узлы, дуги и регионы. Каждый из этих объектов имеет уникальный идентификатор ID, с помощью которого устанавливаются взаимные связи между объектами.

Слой карты, представленный в виде топологической модели данных, называется покрытием. Этот термин происходит из-за того, что взаимное наложение дуг и регионов в модели покрытия не допускается, а вся совокупность регионов в модели вместе с универсальным регионом «покрывает» всю плоскость (рис. 2.7).

Узлы являются обычными точечными объектами, характеризуемыми координатами на плоскости .

Дуги являются линейными объектами – ломаными, соединяющими пару узлов покрытия и проходящими через последовательность промежуточных точек. Кроме того, дуги характеризуются ссылками на два смежных (слева и справа) региона. Между собой дуги одного покрытия пересекаться не могут.

Регионы (области, полигоны) являются площадными объектами. Они характеризуются набором контуров, каждый из которых, в свою очередь, описывается последовательностью дуг покрытия. Между собой регионы одного покрытия пересекаться не могут.

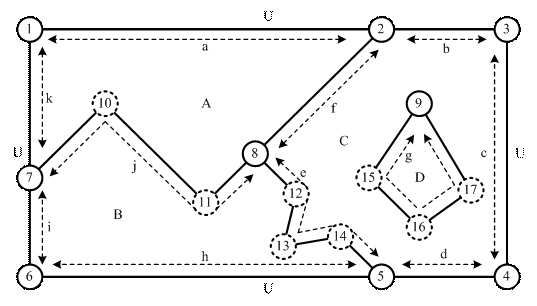
Рис. 2.7. Пример данных модели «покрытия»
(1-9 – узлы, 10-17 – промежуточные точки, a-k – дуги,
A-D – регионы, U – универсальный регион)

Регионы бывают нескольких основных видов:

Простой регион – регион, содержащий только один контур.

Составной регион – регион, содержащий более одного контура. При этом составные регионы могут состоять из топологически несвязанных частей и иметь дырки.

Универсальный регион – часть плоскости, не входящая ни в один регион покрытия. Это понятие является абстракцией и в явном виде неять из топологически которых в свою очередьских изображений представляется в модели покрытия.

2.4. Модель транспортной сети

Модель транспортной (геометрической) сети предназначена, в первую очередь, для описания в виде связанного графа схемы транспортных коммуникаций (автомобильных и железных дорог, авиалиний и водных маршрутов) с целью последующего сетевого анализа.

Транспортная сеть содержит 2 основных типа объектов (узлы и дуги), а также один дополнительный – маршруты (рис. 2.8).

1. Узлы являются обычными точечными объектами, характеризуемыми координатами на плоскости . Узлы могут дополнительно характеризоваться такими параметрами, как запреты на выполнение некоторых поворотов и время их выполнения.

2. Дуги являются линейными объектами – ломаными, соединяющими пару узлов транспортной сети и проходящими через последовательность промежуточных точек. Каждая дуга характеризуется длиной или временем движения по ней, разрешенными направлениями движения, классом дороги или пропускной способностью и др.

3. Дополнительно на транспортной сети могут быть определены объекты еще одного типа – маршруты движения транспорта. Каждый маршрут определяется как замкнутая упорядоченная последовательность узлов и дуг, а также различными числовыми характеристиками (например, расчетное время прохождения транспорта через остановки).

Следует заметить, что модель транспортной сети похожа на модель покрытия без регионов. Однако, в отличие от покрытия, в транспортной сети допустимо взаимное пересечение дуг. Это необходимо, например, чтобы показать пересечение автомобильных дорог в разных уровнях.

Рис. 2.8. Пример данных модели «транспортная сеть»
(1-7 – узлы, 8-12 – промежуточные точки, 7-9 – остановки,
a-n – дуги, A-B – маршруты общественного транспорта)

2.5. Растровая модель данных

Растровая модель данных является исторически самой первой моделью данных геоинформатики. В этой модели вся плоскость разбивается системой равноотстоящих вертикальных и горизонтальных прямых на одинаковые ячейки – пиксели, каждому из которых сопоставлен какой-то код. В каждом пикселе может храниться какая-то числовая характеристика пространства (например, высота рельефа, цвет на фотоснимке, уровень загрязнения окружающей среды) или код объекта, которому принадлежит соответствующий пиксель.

На рис. 2.9 приведен пример представления карты земельных участков в векторной и растровой модели. В векторной модели для каждого полигона A, B, C и D заданы координаты границ полигонов, тектаовой модели данныхсвующий ка пространства, например, цвет ться ближайшим а потом. е. в векторной модели указывается, где находится объект. В растровой модели все пространство разделено на пиксели, в каждом из которых хранится код соответствующего земельного участка, т. е. в растровой модели хранится информация о том, что находится в заданной точке территории.

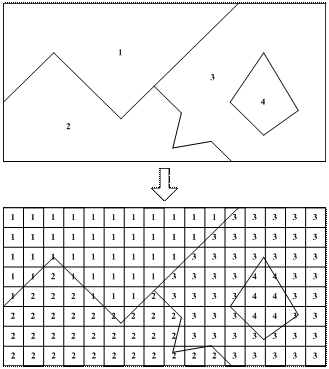
Рис. 2.9. Пример представления земельных участков в векторной (вверху)
и растровой (внизу) модели данных

На примере рис. 2.9 видно, что точность задания границ земельных участков в растровой модели невысока, т. к. соответствует размеру пикселя. Поэтому для повышения точности данных приходится существенно увеличивать количество пикселей. Однако бесконечно увеличивать число пикселей также нельзя, т. к. ресурсы компьютеров ограничены. Например, если бы мы захотели на карте города размером 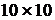 км представить карту земельных участков с точностью 1 см (пикселями размером  см), то нам понадобилось бы  пикселей. Если каждый пиксель мы будем кодировать 4 байтами, то нам понадобится примерно 4 Тб памяти, что значительно превосходит возможности современных компьютеров. Именно поэтому при выборе размера и числа пикселей приходится идти на компромисс.

Для экономии затрачиваемой памяти существуют различные алгоритмические методы компрессии растров, которые позволяют в зависимости от типа данных сжимать их в десятки, сотни и даже тысячи раз. Поэтому в вышеприведенном примере на практике может оказаться достаточно только 1 Гб или даже меньше для хранения вышеуказанной карты земельных участков.

Одним из достоинств растровой модели данных является простота обработки, включая операции пространственного анализа. Например, очень легко можно найти все здания, находящиеся в водоохраной зоне, для чего надо наложить растровые слои зданий и водоохранных зон и попиксельно найти искомые здания.

В настоящее время растровая модель является не основной в ГИС, а используется только в тех случаях, когда векторная модель не даёт адекватного результата. Именно поэтому актуальными являются операции преобразования данных из растра в вектор (векторизация) и наоборот (растеризация). Растеризация – это обычная для ГИС и достаточно простая операция, однако векторизация является гораздо более сложной и большинством ГИС не поддерживается. Векторизация обычно выполняется в ручном или полуавтоматическом режиме с помощью специальных программ – векторизаторов.

Определение. Если ГИС поддерживает только векторные модели данных и нерегулярные сети, то она называется векторной ГИС. Если основной для ГИС является растровая модель данных, то она называется растровой ГИС. Растрово-векторной называется такая растровая ГИС, в которой имеется поддержка векторных моделей и средства векторизации и растеризации.

2.6. Триангуляционная модель поверхностей

Триангуляционная модель данных (нерегулярная триангуляционная сеть, TIN) предназначена для описания поверхностей. В качестве моделируемой поверхности может выступать рельеф земной поверхности (рис. 2.10) или распределение какого-то параметра по земной поверхности, например, загрязнения окружающей среды, количества выпадающих осадков или среднегодовой температуры.

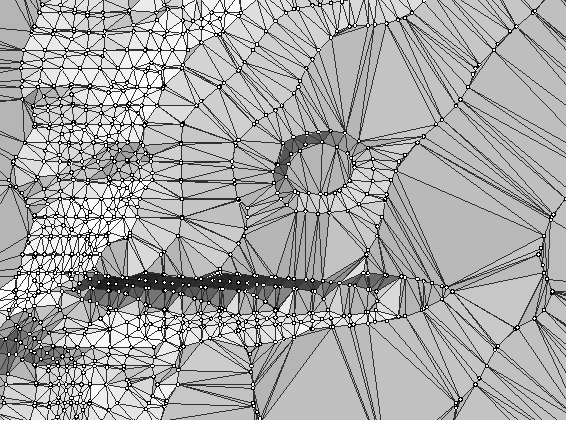
Рис. 2.10. Триангуляционная модель поверхности Земли

Заметим, что для моделирования поверхностей может использоваться и растровая модель, когда в каждом пикселе растра задается высота моделируемой поверхности. Однако триангуляционная модель имеет ряд преимуществ по сравнению с растровой. В первую очередь, это более высокая точность моделирования и обычно меньшие затраты памяти. Во-вторых, в триангуляционной модели можно в явном виде представлять резкие изломы поверхности, т. е. точки и линии, вдоль которых резко меняется кривизна поверхности (вершины гор, границы оврагов, обрывы рек, границы искусственных сооружений). В растровой модели предполагается, что вся моделируемая поверхность является гладкой поверхностью.

Исходными данными для построения триангуляционной модели поверхности служат высотные отметки, изолинии, а также различные структурные линии, меняющие форму поверхности.

В основе триангуляционной модели данных лежит триангуляция – особая структура данных из вычислительной геометрии, определенная на плоскости. В самом общем понимании триангуляция – это планарный граф, построенный на множестве заданных узлов и разбивающий всю плоскость на треугольники и одну внешнюю бесконечную фигуру.

Триангуляция может быть различного вида. В триангуляционной модели данных используется так называемая триангуляция Делоне с ограничениями, в которой треугольники строятся так, чтобы они были «максимально равносторонними», а точнее так, что внутрь окружности, описанной вокруг любого треугольника, по возможности не должны попадать узлы триангуляции (рис. 2.11).

Так как триангуляция определена на плоскости, то для моделирования поверхностей в каждом узле триангуляции дополнительно добавляется еще одна координата – высотная отметка. При этом поверхность как бы «вытягивается из плоскости».

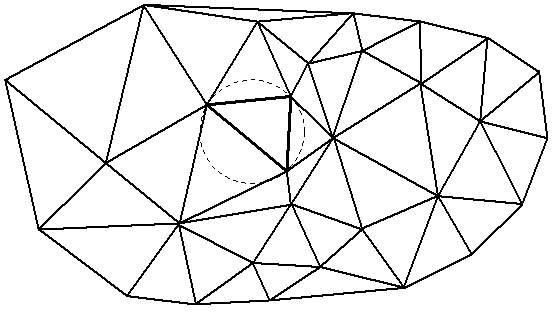
Рис. 2.11. Пример триангуляции Делоне с демонстрацией условия Делоне

Такие триангуляционные модели поверхностей обычно относят к классу так называемых 2,5-мерных моделей, подчеркивая, что, несмотря на наличие z-координат, это не 3-мерная модель, т. к. не любая поверхность может быть описана такой моделью. Например, в этой модели нельзя описать внутреннюю структуру пещеры и склоны горы, являющиеся вертикальными или имеющими отрицательный уклон. На практике, при необходимости моделирования строго вертикальных граней (стены зданий) грани делают «почти» вертикальными, вводя дополнительные узлы в триангуляцию.

Триангуляционная модель данных содержит 3 основных типа данных: узлы, ребра и треугольники (рис. 2.12).

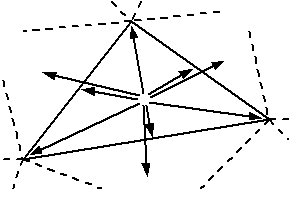
Рис. 2.12. Связи объектов в триангуляционной модели данных

Узлы в триангуляции характеризуются координатами .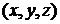

Ребра в триангуляции являются отрезками, соединяющими два некоторые узла. Большинство рёбер в триангуляции в явном виде не представляются, т. к. их можно всегда косвенно получить через треугольники. В явном виде представляются только особые ребра, для которых нужно хранить дополнительную информацию, например, признак структурности линии или то, что поверхность не сохраняет гладкость вдоль этой линии.

Треугольники в триангуляции описываются ссылками на 3 образующих узла, а также ссылками на смежные треугольники и особые ребра. Ссылки на смежные треугольники и ребра нужны только для ускорения операций анализа поверхности, а для отображения на карте не нужны.

2.7. Геореляционная модель данных

Одним из важнейших свойств геоинформационных систем является то, что почти для любого пространственного объекта можно задать набор дополнительных атрибутов в виде числовых или символьных значений.

Последние десятилетия среди множества различных моделей баз данных наиболее распространенной в геоинформатике является так называемая реляционная модель. С точки зрения пользователя вся база данных в этой модели состоит из набора различных таблиц, имеющих фиксированные наборы столбцов (полей), и переменное число строк (записей), описывающих некоторые объекты. Связи между таблицами обеспечиваются с помощью ключевых полей – специально выделенных столбцов таблиц.

В полях реляционных таблиц могут хранится данные только некоторых определенных типов: целые и вещественные числа, строки, логические значения, дата, время, а также большие бинарные массивы (в BLOB-полях).

Для работы с реляционными базами данных разработан специальный язык SQL (язык структурированных запросов), позволяющий выполнять модификацию базы данных, а также выполнять поиск требуемых данных.

На рис. 2.13 представлена простая база данных из двух таблиц, содержащая сведения о земельных участках и их собственниках. Каждая из таблиц содержит ключевое поле (ключ) «ID», уникально определяющее объект «земельный участок» или «собственник» внутри соответствующей таблицы. Связи между таблицами осуществляются с помощью таких ключевых полей. Так, для этого в таблице «Земельный участок» специально выделено поле «Код собственника», в котором запоминается значение ключа из таблицы «Собственник».

Рис. 2.13. Таблицы реляционной базы данных

В дальнейшем при необходимости получения имени собственника для заданного земельного участка система управления базами данных (СУБД) получит код собственника в таблице «Земельный участок», затем найдет в таблице «Собственник» запись с этим кодом и извлечет из соответствующего поля искомое описание собственника.

Одним из недостатков таблицы «Земельный участок» является то, что здесь никак не хранятся сведения о геометрии самого участка. Для этого в соответствии с реляционным подходом следовало было бы завести ряд вспомогательных таблиц и хранить в них необходимую информацию о полигонах, составляющих земельные участки. Однако скорость работы даже самых лучших в мире СУБД не позволит оперативно использовать геометрические данные, представленные в таком виде. «Оперативно» – это когда требуется, например, за доли секунды отрисовать на экране компьютера десятки и сотни тысяч земельных участков.

Именно поэтому в большинстве геоинформационных систем сложился несколько иной – геореляционный подход, когда геометрия пространственного объекта (например, земельного участка) хранится в отдельном месте в специально разработанном формате, а атрибуты объекта – в некоторой таблице базы данных. При этом связь между геометрией и атрибутами осуществляется с помощью ключа – уникального кода пространственного объекта, примерно так же, как и в реляционных таблицах (рис. 2.14).

Рис. 2.14. Геореляционная база данных (слева – упорядоченный
список пространственных объектов в слое карты,
а справа – связанные с ними записи в базе данных)

В геоинформационных системах для удобства пользователей имеется операция соединения атрибутов пространственных данных с таблицами внешних баз данных. В результате пользователю кажется, будто он имеет дело с обычными таблицами баз данных, в которых дополнительно появился первый столбец с геометрией объектов. Для вышеприведенного примера с земельными участками получаемый результат представлен на рис. 2.15.

Рис. 2.15. Соединение таблиц геореляционной базы данных

Теперь, после операции соединения, возможно выполнение операций различных информационных запросов над соединенной таблицей. Например, для земельных участков можно запросить все участки, принадлежащие физическим лицам, и они будут выделены на карте в ГИС.

Другой важной особенностью ГИС после выполнения соединения является автоматическое добавление и удаление записей в присоединенной таблице. Так, при создании на слое карты нового полигона в присоединенной таблице (в нашем примере, в таблице «Земельный участок») будет автоматически создана запись с необходимым значением кода связи ID. При удалении полигона с карты связанная запись будет удалена.

Геореляционный подход в ГИС используется не только для хранения атрибутов для векторных объектов (в шейп-файлах, покрытиях, транспортных сетях и САПР-моделях). Аналогичным способом хранятся данные в растровой модели данных (рис. 2.16).

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20