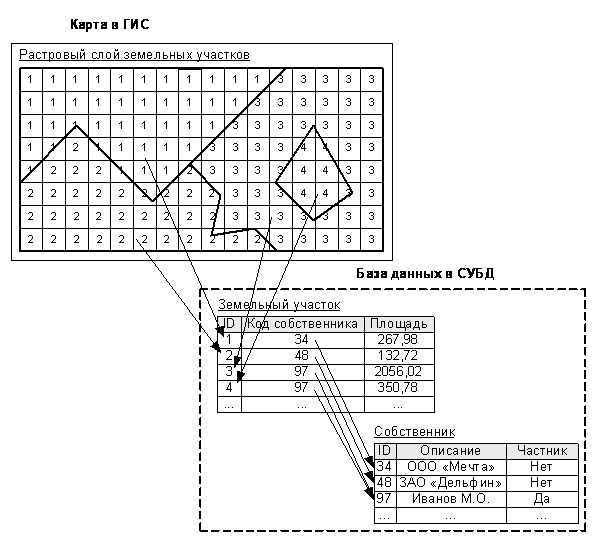
Рис. 2.16. Геореляционная база данных (вверху – растровый слой карты,
снизу – связанные с ними записи в базе данных)

2.8. Геобаза данных

Изначально и до сих пор почти во всех ГИС геометрия и атрибутика пространственных объектов хранятся в различных файлах. Это связано с двумя основными причинами.

Во-первых, это с низкой скоростью извлечения и изменения геометрической информации из баз данных, управляемых обычными системам СУБД, по сравнению с обычными файлами. Отчасти это было связано с низкой пропускной способностью каналов связи между сервером с СУБД, не позволявших передавать с сервера на компьютер пользователя информацию об пространственных объектах, которые должны выводиться на экран практически в реальном режиме времени. Кроме того, низкая скорость связана с тем, что геометрия линейных и площадных объектов должна храниться во вспомогательных таблицах или в BLOB-полях, что также существенно снижает скорость обращения к данным.

Во-вторых, хранение геометрии объектов в базе данных не даёт тех преимуществ, которые имеются при хранении обычных негеометрических данных. Например, в обычных БД имеются несколько ключевых понятий, используемых практически во всех прикладных базах данных. Это «ограничения целостности», не позволяющие вводить некорректные значения в отдельные поля таблиц и создавать некорректные ссылки между таблицами базы данных. Это «блокировки», запрещающие редактировать отдельные поля или целые таблицы базы данных. И это «транзакции», позволяющие выполнять большие изменения БД, но в случае ошибки во время транзакции «откатывающие» состояние всей БД в состояние до её начала.

Но все эти ограничения целостности, блокировки и транзакции мало применимы для пространственных объектов. Так, ограничения целостности в ГИС в основном имеют геометрический характер (например, запрещено пересечение линий дорог и рек, т. к. пересечение рек дорогами должно быть только через мост) и их очень сложно описать стандартными средствами СУБД (в виде хранимых процедур на языке SQL). Блокировки в ГИС должны также иметь пространственный характер, например, для обеспечения возможности параллельной работы многих пользователей с одной картой нужно заблокировать некоторый регион этой карты, что приводит к необходимости блокировки целых таблиц в СУБД.

Классические транзакции в теории баз данных называют также ещё короткими транзакциями, чтобы подчеркнуть, что процесс ввода данных в СУБД обычно занимает немного времени. При этом пока выполняется транзакция одним пользователем, работа другого пользователя должна быть заблокирована, чтобы не нарушить целостность базы данных.

В ГИС же требуется выполнять длинные транзакции, в течение которых пользователь может изменять состояние множества взаимосвязанных слоёв карты. При этом в процессе редактирования многие геометрические ограничения целостности могут нарушаться. По окончании ввода данных (для завершения длинной транзакции) пользователь должен привести базу данных (карту) опять в допустимое состояние. Длинная транзакция может выполняться сколько угодно долгое время (дни и даже недели). Очевидно, что во время ввода данных одним пользователем нельзя блокировать всю базу данных от изменений другими пользователями на столько большое время.

С другой стороны, возможность хранения геометрии совместно с атрибутикой в базе данных принесла бы определенные преимущества, но только если бы удалось решить вышеприведенные проблемы.

В конце концов, всё это привело к разработке различных расширений и надстроек над обычными СУБД, позволяющих создавать полноценные пространственные базы данных, удовлетворяющие всем современным требованиям ГИС. Консорциум разработчиков языка SQL ввёл в последний стандарт языка SQL 3 соответствующие разделы, регламентирующие основы работы с пространственными базами данных.

Самым главным достоинством современных пространственных баз данных является то, что в них можно тесно интегрировать геометрию, атрибутику и поведение объектов. Всё это соответствует основным принципам объектно-ориентированного подхода, являющегося сейчас основным при создании любых программных систем.

В настоящее время наибольшее распространение получили две надстройки над промышленными СУБД, реализующие требования стандарта SQL 3 и тесно интегрированные с ведущими мировыми ГИС. Это ArcSDE (Spatial Database Engine) компании ESRI, Inc (США) и SpatialWare компании MapInfo, Inc (США).

Модель геобазы данных ArcSDE 8.x/9.x является логическим развитием топологической модели данных (покрытия), позволяя создавать при необходимости и аналоги нетопологической модели шейп-файлов. Кроме того, модель геобазы позволяет создавать сети, определять пространственные отношения между объектами, и вводить новые объектно-ориентированные сущности.

Одним из наиболее заметных достижений ArcSDE является введение технологии версий, предназначенных для выполнения «длинные транзакции», и позволяющих отказаться от традиционных блокировок в регионах.

2.9. Вопросы для самопроверки

1. Что такое пространственный объект?

2. Какие бывают модели пространственных данных?

3. Что такое ЦММ, ЦМР?

4. В чем заключается разница между топологической и нетопологической моделями данных?

5. Как представляются объекты в растровой модели данных?

6. Какие модели данных используются для моделирования рельефа?

7. Что такое геореляционная модель данных?

8. Что такое геобаза данных и каковы её основные преимущества перед традиционными моделями данных в файловом исполнении?

Глава 3. Структура и источники геоданных

3.1. Системы координат

Основная цель введения некоторой системы координат в геоинформатике – это описание положения объектов на поверхности Земли в некотором «естественном» виде.

Если мы хотим определить положение судна в океане, и нам нужно проложить маршрут движения по карте, то вначале мы «естественно» должны определить широту и долготу положения судна в градусах с помощью специальных приборов. При этом мы используем географические координаты. Применение таких координат удобно с точки зрения их понимания и вычисления различными астрономическими методами, однако крайне неудобно для выполнения любых геометрических измерений и построений. Например, очень сложно определить кратчайшее расстояние между двумя пунктами на поверхности Земли, положения которых заданы в градусах.

Это связано с тем, что поверхность Земли не является плоскостью, а поэтому формулы вычисления расстояний и других геометрических измерений на реальной поверхности Земли крайне сложны.

В связи с тем, что физическая поверхность Земли имеет очень сложную форму, она в зависимости от решаемых задач аппроксимируется некоторой фигурой, достаточно просто описываемой математически, например, сферой или эллипсоидом. Это позволяет разработать формулы для определения того же самого расстояния на поверхности сферы.

Однако если мы строим новый квартал в городе, то «естественно» предположить, что поверхность Земли в пределах застраиваемой территории является плоской, а потому все сложности сферической геометрии можно отбросить и использовать привычные для всех со школы формулы геометрии на плоскости. Именно поэтому проект внутриквартальной застройки «естественно» выполнить на топографическом плане, используя прямоугольные декартовые координаты в пространстве.

При этом важнейшим вопросом является выбор этой декартовой системы координат. «Естественно» предполагать, что ось Z этой системы координат должна быть направлена вверх, а другие оси – параллельно поверхности Земли в начале координат. Это нужно для того, чтобы можно было в полевых условиях измерять высоты на местности с помощью нивелира, а также определять вертикали с помощью обычного отвеса.

В тоже время, если мы строим большой протяженный объект, например, дорогу, протянувшуюся на сотни или тысячи километров, то поверхность Земли на таких расстояниях будет существенно отличаться от плоскости. Отклонение поверхности Земли от касательной плоскости, в которой определена декартова система координат, составляет на расстоянии 1 км от точки касания 7,8 см, а на 10 км – уже 7,84 м! Поэтому проект строительства дороги будет разбит на участки, выполняемые в различных декартовых системах координат. Основной проблемой такого способа является стыковка участков проекта, выполненных в разных локальных системах координат. Таким образом, возникает необходимость выработки общего подхода, позволяющего легко и непротиворечиво получать локальные системы координат, взаимно увязывать их друг с другом, а также при необходимости переходить к географическим координатам.

Для этого необходимо построить некоторую модель поверхности всей Земли, а также определить формулы перехода от этой модели к локальным координатам и обратно. «Естественно» предполагать, что все локальные (местные) декартовые системы координат должны иметь 1) начала координат, лежащие на модели поверхности Земли, 2) ось Z, направленную по нормали к модели поверхности. При таких предположениях, по крайней мере, измерение вертикали в локальной системе координат можно будет производить на местности с помощью обычного отвеса. Отсюда возникают следующие понятия.

Определение. Уровенной называется поверхность, ортогональная в каждой своей точке к векторами силы тяжести.

Определение. Геоидом называется уровенная поверхность, проходящая через некоторую точку начала отсчета высот.

Однако геоид имеет крайне сложную форму и её практически невозможно математически точно описать. Поэтому, в зависимости от решаемых задач, форма геоида может аппроксимироваться сферой, эллипсоидом вращения, трехосным эллипсоидом или, наиболее точно, квазигеоидами.

Сложность формы геоида (как и любой другой уровенной поверхности) возникает из-за того, что Земля состоит из неравномерно распределенных масс различной плотности. Это приводит к тому, что сила тяжести на поверхности Земли в разных местах является различной. Кроме того, вектора силы тяжести направлены в самые разные направления, не сходящиеся в центре масс Земли.

Определение. Общеземным называется эллипсоид вращения, плоскость экватора и центр которого совпадают с плоскостью экватора и центром масс Земли, и наилучшим образом аппроксимирующий поверхность геоида.

Определение. Референц-эллипсоидом называется такой эллипсоид, который наилучшим образом аппроксимирует поверхность геоида на соответствующей территории Земли.

Определение. Квазигеоидом называется такая фигура, которая на различных участках поверхности Земли аппроксимируется различными местными референц-эллипсоидами. На территории морей и океанов поверхность квазигеоида совпадает с поверхностью геоида, а на суше она отклоняется от него в пределах двух метров.

Большинство референц-эллипсоидов являются эллипсоидами вращения, которые характеризуются длинами своих полуосей (a – расстояние от его центра до точек экватора и b – расстояние от центра до полюсов) и вытекающим из этих длин коэффициентом сжатия  (рис. 3.1). Вместо коэффициента сжатия эллипсоиды иногда характеризуют эксцентриситетом .

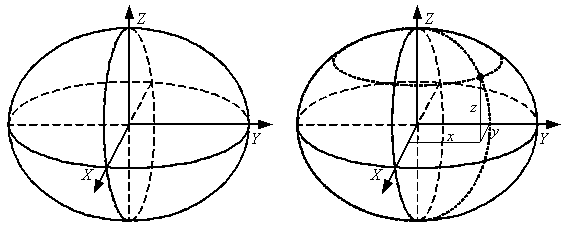
Рис. 3.1. Эллипсоид вращения

Кроме своих размеров референц-эллипсоиды характеризуются положением центра в теле Земли и ориентацией вертикальной оси. Когда для работы на территории берется некоторый местный референц-эллипсоид, то он выбирается так, чтобы максимально точно соответствовать поверхности геоида на этой территории (рис. 3.2). Именно поэтому данный референц-эллипсоид может очень сильно отличаться от поверхности геоида на других территориях.

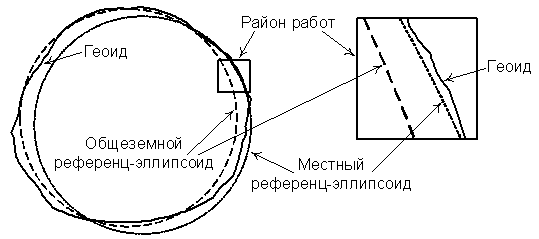
Рис. 3.2. Аппроксимация поверхности Земли референц-эллипсоидами

Среди множества имеющихся в мире референц-эллипсоидов в России наиболее часто используется эллипсоид Красовского (   ), начальный пункт в Пулково, превышение геоида над референц-эллипсоидом в начальном пункте равно нулю, а измерение высот делается в Балтийской системе высот, ведущей отсчет от нуля Кронштатского футштока. Эта система координат называется СК-42, т. к. она была разработана в 1942 г., а с 1946 г. была введена в эксплуатацию на территории СССР. Тем не менее, на Дальнем Востоке иногда используется другая система высот от уровня Охотского моря.

В России с 1 июля 2002 г. обязательным к применению является система координат СК-95 (на основе эллипсоида Красовского, но несколько смещенного и повернутого относительно СК-42) для всех геодезических и картографических работ, а для геодезического обеспечения орбитальных полетов – ПЗ-90 (Параметры Земли 1990 г.), имеющая параметры     .

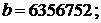
Тем не менее, в последнее время в России все чаще стал также применяться референц-эллипсоид WGS-84 (   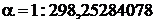). Это связано с тем, что в системе этого референц-эллипсоида выдают координаты приемники американской системы глобального позиционирования GPS, которая всё шире применяется в практике геодезических работ.

В математической картографии используются пространственные прямоугольные, криволинейные, плоские прямоугольные и полярные системы координат.

Самой простой является пространственная прямоугольная геоцентрическая система координат, начало которой совмещено с центром Земли, ось Z направлена на Северный полюс Земли, ось X – на точку пересечения Гринвичского меридиана с экватором, а ось Y – на восток от Гринвича (рис. 3.3). В качестве точки Северного полюса обычно используют условный земной полюс (международное условное начало), которая вместе с центром масс Земли определяет некоторое фиксированное среднее положение оси вращения Земли. Это связано с тем, что ось вращения Земли со временем перемещается в теле Земли и относительно звезд.

В то же время на практике обычно используются различные квазигеоцентрические системы координат, центр которых и угол наклона осей несколько иной. Именно поэтому имеются специальные формулы для пересчета координат из одной системы координат в другую:

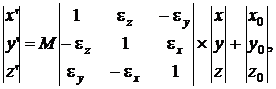
где 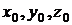 – координаты начала координат второй системы в первой, M – масштабный коэффициент,  – разворот осей на малые углы.

Ориентация используемого референц-эллипсоида характеризуется смещением от центра масс Земли и отклонением его оси относительно оси вращения Земли.

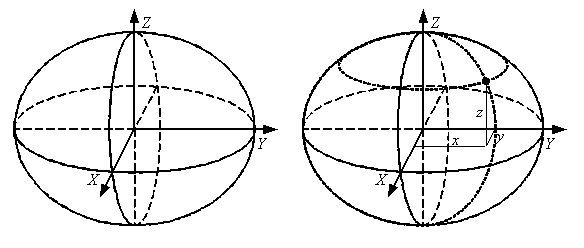
Рис. 3.3. Геоцентрическая система координат

Однако более привычной является географическая (геодезическая) система координат, когда координаты точки на поверхности эллипсоида определяются широтой  и долготой, измеряемыми в градусах от экватора и от Гринвичского меридиана соответственно (рис. 3.4). Координаты любой точки в пространстве складываются из широты и долготы её проекции по нормали на эллипсоид и высоты H точки относительно эллипсоида.

В связи с тем, что широта и долгота точки на местности зачастую определяется с помощью астрономических наблюдений, географические координаты также иногда называются астрономическими.

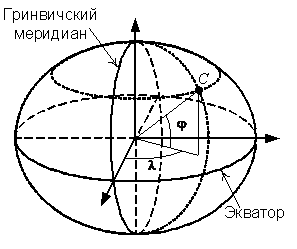
Рис. 3.4. Географическая (геодезическая) система координат

Использование вышеприведенных геоцентрической и географической систем координат не всегда удобно. Так, при работе на небольших участках земной поверхности обычно используется топоцентрическая (горизонтная) система координат, которая является обычной прямоугольной пространственной системой координат и характеризуется некоторой начальной точкой , задаваемой в географической системе координат ( – это высота точки  над уровнем референц-эллипсоида). Ось Z топоцентрической системы координат совпадает с нормалью к поверхности эллипсоида, проходящей через , ось X лежит в плоскости меридиана и направлена на северный полюс, а ось Y направлена на восток  (рис. 3.5).

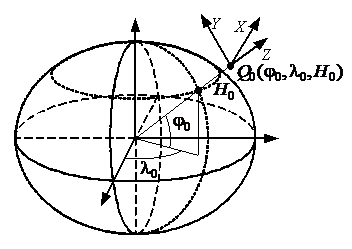
Рис. 3.5. Топоцентрическая (горизонтная) система координат

Кроме вышеупомянутых также широко используется  полярная сфероидическая (сферическая) система координат. В этой системе отсчет ведется от точки нового полюса , задаваемого в географической системе координат (рис. 3.6). Положение любой точки C на поверхности эллипсоида задается двумя углами a и z. Угол a (азимут) измеряется между нормальными плоскостями в точке полюса, одна из которых проходит через старые полюса эллипсоида, а другая – через точку C. Угол z определяется как , где точка  является точкой пересечения вертикальной оси референц-эллипсоида с нормалью к эллипсоиду, проведенной через точку нового полюса. Слово полярная в названии данной системы координат призвано подчеркнуть, что координаты a и z можно представлять себе как полярные угол и радиус соответственно, только на поверхности эллипсоида, а не на плоскости.

Рис. 3.6. Полярная сфероидическая (сферическая) система координат

Отметим, что в математической картографии иногда также используется «почти обычная» полярная система координат – так называемая полярная геодезическая система координат. В этой системе отсчет, также как и в предыдущем случае, ведется от точки нового полюса , задаваемого в географической системе координат (рис. 3.76). Положение любой точки C на поверхности эллипсоида задается длиной геодезической линии s от  до C и азимутом a – углом между нормальными плоскостями в точке полюса, одна из которых проходит через старые полюса эллипсоида, а другая – через точку C (геодезической линией между двумя заданными точками на некоторой поверхности называется кратчайшая линия, связывающая эти две точки по этой поверхности).

Рис. 3.7. Полярная геодезическая система координат

Все вышеприведенные системы координат предназначены для задания «абсолютных координат», т. е. координат, не зависящих от положения никаких объектов в пространстве.

В противовес абсолютным часто используются различные относительные координаты, в которых отсчет ведется от некоторых заметных объектов на местности.

Относительные координаты бывают двух основных видов:

1. Относительная полюсная система координат. В этих координатах отсчет ведется от полюсов – некоторых известных точек на местности, заданных либо в абсолютной системе координат, либо в описательном виде. Положение любой иной точки на местности может задаваться как азимут и расстояние от некоторого полюса, либо как расстояния от двух полюсов.

С помощью таких координат очень часто задается положение объектов подземных инженерных коммуникаций (колодцев, труб, кабелей) на картах местности, например, в терминах «4 метра на север от угла дома» или «в 5 метрах от угла дома и на расстоянии 6 метров от стены трансформаторной подстанции» (рис. 3.8).

Эта система координат позволяет задать положение объектов на плане, а также в пространстве, добавляя в описание координат смещение по высоте искомой точки от плановой («2 метра под землей») или от базовой точки («3 метра ниже отметки на стене дома»).

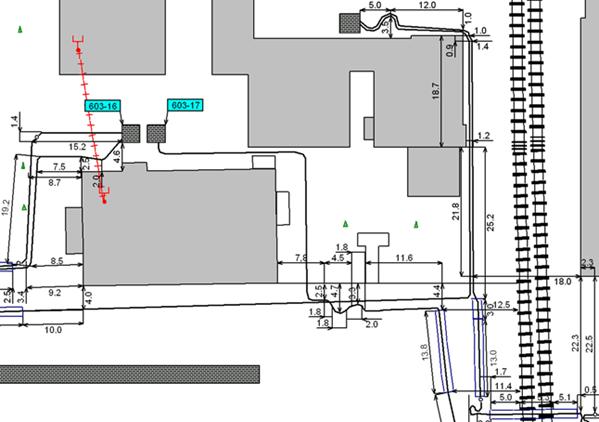
Рис. 3.8. Задание положения инженерных коммуникацией
с помощью относительной полюсной системы координат

2. Относительная линеаризованная (пикетажная) система координат. В этой системе за основу берется некоторая базовая кривая, положение которой задано в абсолютной системе координат. Кроме того, на этой кривой выбирается некоторая базовая точка B (обычно это начало кривой). Положение любой иной точки C на базовой кривой считается как кратчайшее расстояние от этой точки до базовой точки вдоль базовой кривой. Такое расстояние часто называют пикетажным расстоянием или пикетажем. Для определения положения любой точки P на плоскости, не лежащей на базовой прямой, нужно найти ближайшую точку С на базовой прямой. Положением точки P будет считаться пара величин «пикетаж + смещение», где «пикетаж» – это пикетаж точки С относительно B, а «смещение» – это расстояние от P до C. Причем, если точка P располагается справа от кривой BC, то смещение берется со знаком плюс, иначе – со знаком минус (рис. 3.9).

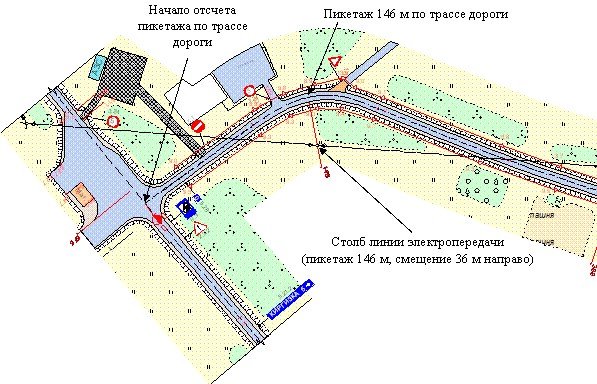
Рис. 3.9. Задание положения объектов инженерного обустройства
автомобильной дороги с помощью линеаризованной системы координат

3.2. Картографические проекции

В связи с тем, что форма Земли не является плоской, при построении бумажных или электронных карт используются так называемые картографические проекции – математические способы отображения поверхности Земли на плоскость.

К настоящему времени создано огромное количество различных проекций, выбор которых для применения зависит от размеров картографируемой территории, назначения карты и стандартов, принятых в той или иной стране.

Одной из важнейших характеристик проекций является характер и величина искажений. При этом выделяют следующие виды проекций:

1. Равноугольные проекции. В этих проекциях сохраняются без искажений углы и формы малых объектов, но сильно искажаются длины и площади объектов. В математике такие преобразования называются конформными. Такие проекции используются, например, для навигации и прокладки транспортных маршрутов.

2. Равновеликие проекции. Эти проекции сохраняют площади всех объектов, но искажают углы и формы объектов. В таких проекциях очень удобно, например, определять площади земельных участков.

3. Равнопромежуточные проекции. В этих проекциях сохраняются длины вдоль одного из главных направлений (обычно вдоль параллелей либо вдоль одного или всех меридианов).

4. Произвольные проекции. В таких проекциях не сохраняются длины, площади или углы, однако преобразование проекции подбирается так, чтобы искажения углов, площадей и длин были в целом по карте минимальны. Обычно в центре карты делают минимальные искажения, которые плавно возрастают к краям.

Картографические проекции обычно задаются в виде:

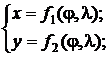
где x – вертикальная (не горизонтальная!) координата после проецирования; y – горизонтальная координата;  – широта проецируемой точки;  – долгота.

В зависимости от общего вида функций  и  получаются различные семейства проекций. Рассмотрим основные классы проекций.

1. Цилиндрические проекции. В этих проекциях меридианы – это равноотстоящие параллельные линии, а параллели – параллельные прямые, ортогональные меридианам. Общие уравнения цилиндрических проекций выглядят так:

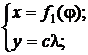
где c – постоянный параметр.

Различные варианты цилиндрической проекции приведены на рис. 3.10–3.12.

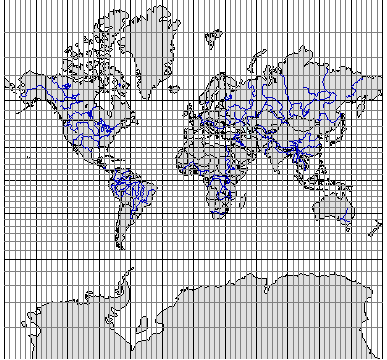
Рис. 3.10. Равноугольная цилиндрическая проекция

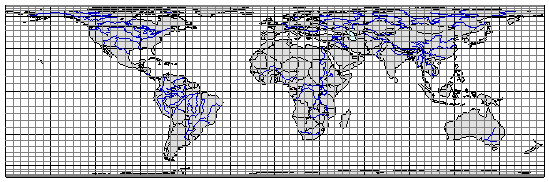
Рис. 3.11. Равновеликая цилиндрическая проекция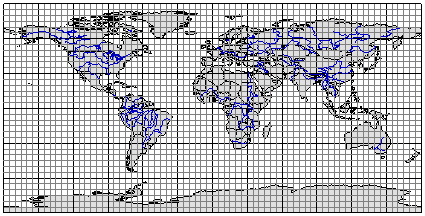

Рис. 3.12. Равнопромежуточная по меридианам цилиндрическая проекция

2. Псевдоцилиндрические проекции. В этих проекциях параллели – это параллельные прямые, а меридианы – кривые или прямые, симметричные относительно среднего прямолинейного меридиана.

Общие уравнения псевдоцилиндрических проекций выглядят так:

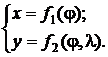
Варианты равновеликих псевдоцилиндрических проекций приведены на рис. 3.13–3.15 с меридианами в форме синусоид, а на рис. 3.16 – с меридианами в форме эллипсов. На рис. 3.17–3.19 приведены примеры произвольных псевдоцилиндрических проекций.

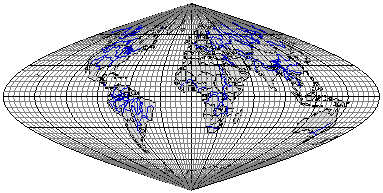
Рис. 3.13. Равновеликая синусоидальная псевдоцилиндрическая проекция
с полюсами в виде точек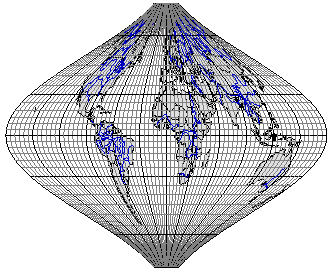

Рис. 3.14. Равновеликая синусоидальная псевдоцилиндрическая проекция
с полярной линией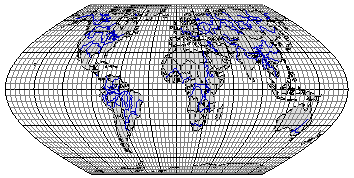

Рис. 3.15. Равновеликая синусоидальная псевдоцилиндрическая
проекция Каврайского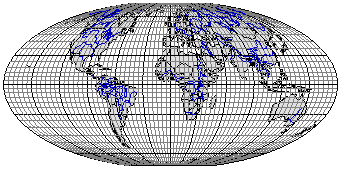

Рис. 3.16. Равновеликая эллиптическая псевдоцилиндрическая
проекция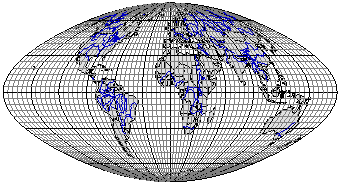

Рис. 3.17. Произвольная синусоидальная псевдоцилиндрическая
проекция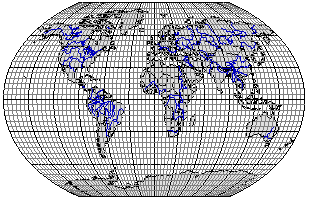

Рис. 3.18. Произвольная эллиптическая псевдоцилиндрическая
проекция Каврайского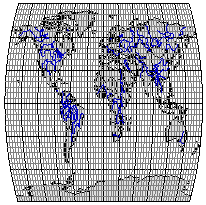

Рис. 3.19. Произвольная эллиптическая псевдоцилиндрическая
проекция Михайлова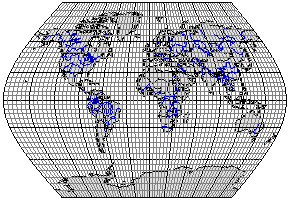

Рис. 3.20. Произвольная псевдоцилиндрическая
проекция ЦНИИГАиК (Гинзбурга)

3. Поперечно-цилиндрические. Для получения этих проекций вначале географические координаты переводятся в сферические полярные координаты, которые в свою очередь преобразуются с помощью некоторой обычной цилиндрической проекции. К этим проекциям относятся наиболее распространенные в мире проекции: проекции Гаусса-Крюгера и UTM.

Общие уравнения поперечно-цилиндрических проекций выглядят следующим образом:

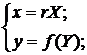
где X, Y – сферические полярные координаты поперечной системы, а r – константа.

Примеры некоторых поперечно-цилиндрических проекций приведены на рис. 3.21–3.22.

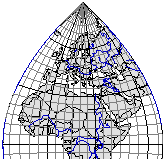
Рис. 3.21. Поперечно-цилиндрическая проекция Гаусса-Крюгер. Практически
также выглядят проекции Кассини-Зольднера, Гаусса-Ламберта, а также
Меркатора, которая известна также как UTM или проекция Гаусса-Боага

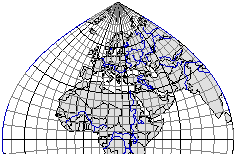
Рис. 3.22. Поперечно-цилиндрическая проекция Гаусса-Крюгера для широкой полосы

4. Конические проекции. В этих проекциях параллели – это концентрические окружности, а меридианы – пучок прямых, проведенных из центра окружностей.

Общие уравнения конических проекций выглядят так:

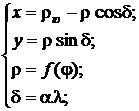
где  – полярный радиус южной параллели, а .

Варианты равноугольных конических проекций приведены на рис. 3.23–3.24.

Рис. 3.23. Равноугольная коническая проекция с одинаковыми
искажениями на крайних параллелях 10° и 80°

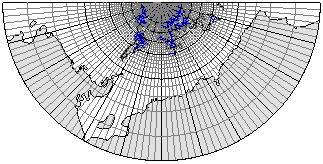
Рис. 3.24. Равноугольная коническая проекция

5. Псевдоконические проекции. В этих проекциях параллели  – это дуги концентрических окружностей, а меридианы – кривые, симметричные относительно среднего прямолинейного меридиана, на котором расположен центр параллелей.

Общие уравнения псевдоконических проекций выглядят так:

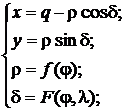
где q – полярное расстояние южной параллели на плоскости.

Примеры псевдоконических проекций приведены на рис. 3.25–3.26.

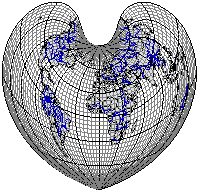
Рис. 3.25. Равновеликая псевдоконическая проекция Бонна
(стандартная параллель = 50°)

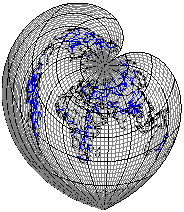
Рис. 3.26. Псевдоконическая проекция Штаба-Вернера (серцевидная).
Искажения отсутствуют на среднем меридиане (55°) и северном полюсе

6. Поликонические проекции. В этих проекциях параллели  – это дуги эксцентрических окружностей с центрами, расположенными на среднем прямолинейном меридиане, а меридианы – кривые, симметричные относительно среднего меридиана и экватора.

Общие уравнения поликонических проекций выглядят так:

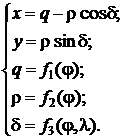
Варианты поликонических проекций приведены на рис. 3.27–3.31.

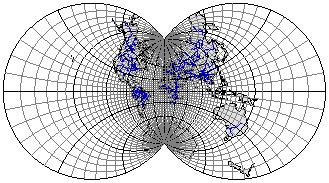
Рис. 3.27. Поликоническая проекция Лагранжа

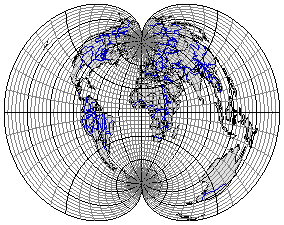
Рис. 3.28. Простая поликоническая проекция

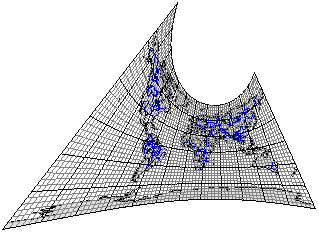
Рис. 3.29. Видоизмененная простая поликоническая проекция

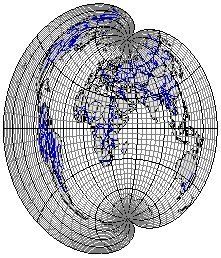
Рис. 3.30. Равновеликая поликоническая проекция

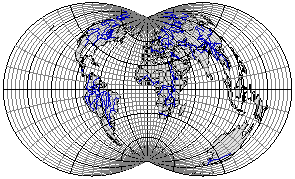
Рис. 3.31. Ортогональная поликоническая проекция

7. Азимутальные проекции. В этих проекциях параллели (альмукантараты) – это концентрические окружности, а меридианы (вертикалы) – прямые линии, пересекающиеся в центре окружностей под углами, равными разностям долгот соответствующих меридианов.

Общие уравнения азимутальных проекций выглядят так:

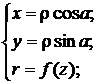
где z, a – сферические полярные координаты точек .

Варианты азимутальной проекций приведены на рис. 3.32–3.35.

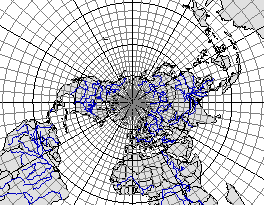
Рис. 3.32. Равноугольная азимутальная проекция

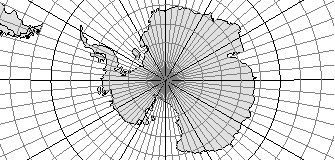
Рис. 3.33. Равноугольная азимутальная проекция
для изображения полярных областей

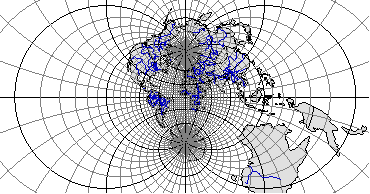
Рис. 3.34. Равноугольная азимутальная проекция для изображения территорий
с округлыми очертаниями (кроме полярных областей)

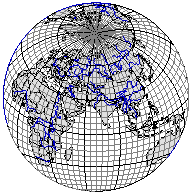
Рис. 3.35. Равновеликая азимутальная проекция шара Ламберта. Аналогично выглядит проекция Постеля (в ней также отсутствуют искажения вдоль стандартной параллели)

8. Псевдоазимутальные проекции. Такие проекции применяются в случаях, когда нужно передать на карте эффект сферичности Земли. В этих проекциях параллели  – это концентрические окружности, а меридианы – кривые или прямые, сходящиеся в центре параллелей. При этом меридианы 0° и 360° совпадают.

Общие уравнения псевдоазимутальных проекций выглядят так:

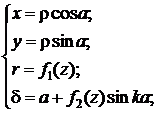
где z, a – сферические полярные координаты точек ; k и a – константы.

Примеры псевдоазимутальных проекций приведены на рис. 3.36–37.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20