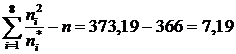 .
.
Следовательно, вычисления проведены правильно.
Найдем число степеней свободы: S = 8, k = 8 – 3 = 5. По таблице критических точек распределения χ2 по уровню значимости α = 0,05 и числу степеней свободы 5 находим χ2кр(0,05;5) = 11,1. Так как χ2набл > χ2кр, то нет оснований отвергнуть нулевую гипотезу. Другими словами, расхождение эмпирических и теоретических частот незначительное. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.
ЭЛЕМЕНТЫ КОРРЕЛЛЯЦИОННОГО АНАЛИЗА
Функциональная, стохастическая и корреляционная зависимости.
Две случайные величины могут быть связаны либо функциональной зависимостью, либо зависимостью другого рода, называемой стохастической, либо быть независимыми.
Строгая функциональная зависимость (детерминированные величины) реализуется сравнительно редко, поскольку обе величины, или одна из них, подвержены действию случайных факторов, причем среди них могут быть и общие для обеих величин. В этом случае возникает стохастическая зависимость, которую в некоторых случаях называют статистической.
Стохастической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой.
Стохастическую зависимость называют корреляционной, если при изменении одной из величин изменяется среднее значение другой.
Например, если Y – прибыль некоторой организации, а Х – размер вложенных ресурсов, то для одинаковых по объему производства и типам товаров организаций величина прибыли может существенно отличаться, т. е. Y – не функция Х. Это объясняется влиянием множества случайных факторов (конъюнктурой рынка, квалификацией персонала, геополитическим и физико-климатическим расположением организаций). Вместе с тем, как показывает опыт, среднее значение прибыли зависит от вложенных ресурсов, т. е. величины Х и Y связаны корреляционной зависимостью.
Параметры выборочного уравнения регрессии.
Условное математическое ожидание М (Y / Х = х) является функцией от ![]() , следовательно, его оценка, т. е. условное среднее
, следовательно, его оценка, т. е. условное среднее ![]() , также является функцией от
, также является функцией от ![]() . Если обозначить эту функцию через
. Если обозначить эту функцию через ![]() , то получим уравнение
, то получим уравнение ![]() . Это уравнение принято называть выборочным уравнением регрессии Y на Х, саму функцию
. Это уравнение принято называть выборочным уравнением регрессии Y на Х, саму функцию ![]() – выборочной регрессией Y на Х, а ее график – выборочной линией регрессии Y на Х. Из соображений симметрии можно говорить и о регрессии Х на Y.
– выборочной регрессией Y на Х, а ее график – выборочной линией регрессии Y на Х. Из соображений симметрии можно говорить и о регрессии Х на Y.
Расчет параметров по не сгруппированным данным.
Пусть имеются две случайные величины Х, Y и в результате ![]() независимых опытов получены
независимых опытов получены ![]() пар независимых чисел
пар независимых чисел ![]() . Найдем линейное выборочное уравнение регрессии Y на Х в виде
. Найдем линейное выборочное уравнение регрессии Y на Х в виде ![]() . Поскольку по выборочным данным можно получить только оценки параметров, то оценку коэффициента
. Поскольку по выборочным данным можно получить только оценки параметров, то оценку коэффициента ![]() обозначим через
обозначим через ![]() , а оценку
, а оценку ![]() – через
– через ![]() , т. е.
, т. е. ![]() . Подберем параметры
. Подберем параметры ![]() и
и ![]() так, чтобы точки, построенные по данным наблюдений лежали как можно ближе к прямой. С этой целью используется метод наименьших квадратов. Обозначим через
так, чтобы точки, построенные по данным наблюдений лежали как можно ближе к прямой. С этой целью используется метод наименьших квадратов. Обозначим через ![]() значение величины Y, соответствующее
значение величины Y, соответствующее ![]() , а через
, а через ![]() – значение
– значение ![]() , которое может быть получено из последнего равенства при
, которое может быть получено из последнего равенства при ![]() . Возьмем разности
. Возьмем разности ![]() , возведем их в квадрат и просуммируем. В результате получим функцию:
, возведем их в квадрат и просуммируем. В результате получим функцию:
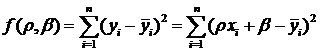
Найдя частные производные этой функции по ![]() и
и ![]() и используя необходимое условие экстремума функции, получим:
и используя необходимое условие экстремума функции, получим:
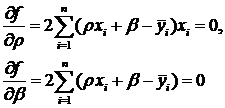
Эти уравнения можно привести к виду:
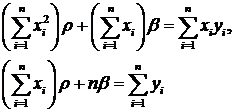
Решая эту систему уравнений относительно ![]() и
и ![]() , получим:
, получим:
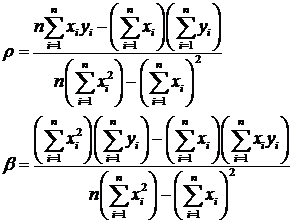
Пример. Найти выборочное уравнение прямой линии регрессии Y на Х по данным ![]() наблюдений:
наблюдений:
| 1,0 | 1,5 | 3,0 | 4,5 | 5,0 |
| 1,25 | 1,40 | 1,50 | 1,75 | 2,25 |
Составим расчетную таблицу:
|
|
|
|
|
1 | 1,0 | 1,25 | 1,00 | 1,25 |
2 | 1,5 | 1,40 | 2,25 | 2,10 |
3 | 3,0 | 1,50 | 9,00 | 4,50 |
4 | 4,5 | 1,75 | 20,25 | 7,875 |
5 | 5,0 | 2,25 | 25,00 | 11,25 |
Σ | 15,0 | 8,15 | 57,50 | 26,975 |
Найдем искомые параметры:
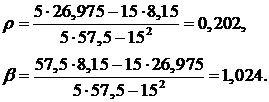
Тогда искомое уравнение будет иметь вид:
![]() .
.
Для того, чтобы получить представление, насколько хорошо вычисленные по этому уравнению значения ![]() согласуются с наблюдаемыми значениями
согласуются с наблюдаемыми значениями ![]() , находят их разность
, находят их разность ![]() , характеризующую отклонение.
, характеризующую отклонение.
| 1,226 | 1,327 | 1,63 | 1,933 | 2,034 |
| 1,25 | 1,40 | 1,50 | 1,75 | 2,25 |
| -0,024 | -0,073 | 0,13 | 0,183 | -0,216 |
Как видно из примера, не все отклонения достаточно малы, что объясняется малым числом наблюдений.
Расчет параметров по сгруппированным данным
При большом числе опытов одно и то же значение ![]() может встретиться
может встретиться ![]() раз, а одно и то же значение
раз, а одно и то же значение ![]() соответственно
соответственно ![]() раз. Одна и та же пара значений
раз. Одна и та же пара значений ![]() может наблюдаться
может наблюдаться ![]() раз. Поэтому наблюдаемые значения могут быть сгруппированы. Для этого подсчитываются все частоты и результаты заносят в таблицу, называемую корреляционной. В этой таблице на пересечении строк и столбцов, т. е. для каждой пары значений
раз. Поэтому наблюдаемые значения могут быть сгруппированы. Для этого подсчитываются все частоты и результаты заносят в таблицу, называемую корреляционной. В этой таблице на пересечении строк и столбцов, т. е. для каждой пары значений ![]() , указывается частота
, указывается частота ![]() . При этом прочерк означает, что такая пара значений не наблюдалась вовсе. Очевидно, что:
. При этом прочерк означает, что такая пара значений не наблюдалась вовсе. Очевидно, что:
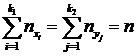 .
.
Пусть составлена корреляционная таблица наблюдаемых значений Х и Y.
Тогда очевидна справедливость выражений:
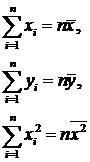
Кроме того:
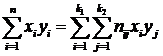 ,
,
где ![]() – число значений
– число значений ![]() ;
; ![]() – число значений
– число значений ![]() .
.
Заменив в системе уравнений для нахождения ![]() и
и ![]() по не сгруппированным данным соответствующие суммы полученными выражениями, имеем:
по не сгруппированным данным соответствующие суммы полученными выражениями, имеем:
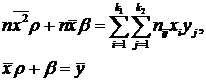
Решая эту систему, находят значения ![]() и
и ![]() , которые затем подставляют в исходное уравнение регрессии.
, которые затем подставляют в исходное уравнение регрессии.
Однако чаще уравнение регрессии записывают в другом виде с использованием выборочного коэффициента корреляции. Для этого из второго уравнения системы найдем ![]() и подставим в исходное уравнение регрессии
и подставим в исходное уравнение регрессии ![]() . Поскольку
. Поскольку ![]() , то:
, то:
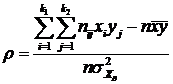 .
.
Умножив обе части на ![]() , получим:
, получим:
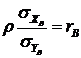 .
.
Здесь ![]() и есть выборочный коэффициент корреляции.
и есть выборочный коэффициент корреляции.
Таким образом:
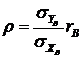 .
.
Следовательно:
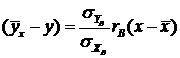 .
.
Выборочный коэффициент корреляции.
Выборочный коэффициент корреляции определяется равенством:
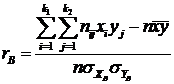
Известно, что если величины Х и Y независимы, то коэффициент корреляции равен нулю. Если же он равен единице (с любым знаком), то эти же величины связаны линейной функциональной зависимостью. Отсюда следует, что коэффициент корреляции измеряет силу (или тесноту) линейной связи между величинами Х и Y.
Поскольку выборочный коэффициент корреляции равен ![]() является оценкой коэффициента корреляции
является оценкой коэффициента корреляции ![]() генеральной совокупности, он также служит для измерения силы линейной связи между количественными признаками Y и Х. Допустим, что выборочный коэффициент корреляции, найденный по выборке, оказался отличным от нуля. Так как выборка отобрана случайным образом, то нельзя однозначно заключить, что коэффициент корреляции генеральной совокупности также отличен от нуля. Возникает необходимость проверки гипотезы (предположения) о значимости (существенности) выборочного коэффициента корреляции или, что одно и то же, о равенстве нулю коэффициента корреляции генеральной совокупности. Если после соответствующей проверки гипотеза о равенстве нулю генерального коэффициента корреляции будет отвергнута, то выборочный коэффициент корреляции значим, а величины Х и Y коррелированы. В противном случае этот коэффициент незначим.
генеральной совокупности, он также служит для измерения силы линейной связи между количественными признаками Y и Х. Допустим, что выборочный коэффициент корреляции, найденный по выборке, оказался отличным от нуля. Так как выборка отобрана случайным образом, то нельзя однозначно заключить, что коэффициент корреляции генеральной совокупности также отличен от нуля. Возникает необходимость проверки гипотезы (предположения) о значимости (существенности) выборочного коэффициента корреляции или, что одно и то же, о равенстве нулю коэффициента корреляции генеральной совокупности. Если после соответствующей проверки гипотеза о равенстве нулю генерального коэффициента корреляции будет отвергнута, то выборочный коэффициент корреляции значим, а величины Х и Y коррелированы. В противном случае этот коэффициент незначим.
Если выборка имеет достаточно большой объем и репрезентативна (от фр., то заключение о тесноте линейной зависимости между признаками, полученное по данным выборки, в известной степени может быть распространено и на генеральную совокупность. Например, для оценки коэффициента корреляции ![]() нормально распределенной генеральной совокупности (при
нормально распределенной генеральной совокупности (при ![]() ) можно использовать следующую зависимость:
) можно использовать следующую зависимость:
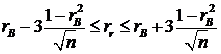 .
.
Выборочное корреляционное отношение.
Рассмотренный выборочный коэффициент корреляции служит только для оценки тесноты линейной корреляционной связи. Тогда возникает вопрос о возможности оценки любой корреляционной связи.
Пусть данные наблюдений над количественными признаками Х и Y сведены в корреляционную таблицу. Можно считать, что наблюдаемые значения Y разбиты на группы, причем каждая группа содержит те значения Y, которые соответствуют определенному значению Х. Тогда условные средние можно назвать групповыми средними.
Поскольку все значения признака разбиты на группы, можно представить общую дисперсию признака в виде суммы внутригрупповой и межгрупповой дисперсий ![]() . Учитывая это обстоятельство, сформулируем два важных утверждения.
. Учитывая это обстоятельство, сформулируем два важных утверждения.
1. Если признак Y связан с признаком Х функциональной зависимостью, то выполняется соотношение ![]() .
.
2. Если Y связан с Х корреляционной зависимостью, то выполняется соотношение ![]() .
.
Из приведенных рассуждений следует, что целесообразно в качестве меры тесноты корреляционной связи рассматривать отношение межгрупповой дисперсии к общей.
Выборочным корреляционным отношением Y и Х называется отношение межгруппового среднего квадратичного отклонения к общему среднему квадратичному отклонению признака Y, т. е.
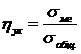 ,
,
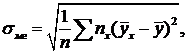
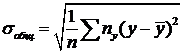
где ![]() и
и ![]() – частоты значения признака Х и Y соответственно.
– частоты значения признака Х и Y соответственно.
Перечислим основные свойства выборочного корреляционного отношения.
1. Выборочное корреляционное отношение удовлетворяет двойному неравенству ![]() .
.
2. Если ![]() , то Y и Х корреляционной зависимостью не связаны.
, то Y и Х корреляционной зависимостью не связаны.
3. Если ![]() , то Y и Х связаны функциональной зависимостью.
, то Y и Х связаны функциональной зависимостью.
4. Выборочное корреляционное отношение не меньше абсолютной величины выборочного коэффициента корреляции, т. е. ![]() .
.
5. Если выборочное корреляционное отношение равно абсолютной величине выборочного коэффициента корреляции, то имеет место точная линейная корреляционная зависимость.
ЛИТЕРАТУРА.
1. Высшая математика для экономистов: Учебник для студентов вузов, обучающихся по экономическим специальностям / Под редакцией проф. . – 3-е изд. – М.: ЮНИТИ-ДАНА, 2009. – 479 с.
2. Высшая математика для экономистов: Практикум для студентов вузов, обучающихся по экономическим специальностям; под ред. проф. . – 2-е изд., перераб. и доп. – М.: ЮНИТИ-ДАНА, 2007. – 479 с.
3. Общий курс высшей математики для экономистов: Учебник / Под общ. ред. – М.: ИНФРА-М, 2008. – 656 с.
4. Сборник задач по высшей математике для экономистов: Учебное пособие / Под редакцией . - М.: ИНФРА-М, 2003. – 275 с.
5. Шипачев математика. Учебник для вузов. – 7-е изд. стер. – М.: Высшая школа, 2005. – 479 с.
6. Шипачев по высшей математике. – 3-е изд. стер. – М.: Высшая школа, 2003. – 304 с.
7. , Куркина математика: Учебник – 3-е изд. – М.: ТК Велби, Изд-во Проспект, 2008. – 600 с.
8. Малыхин в экономике: Учебное пособие. - М.: ИНФРА-М, 2002. – 352 с.
9. Овсянников алгебра. Учебное пособие для студентов вузов. – Гуманитарный университет – Екатеринбург, 2004. – 293с.
10. , Сборник задач по математике. Учебное пособие. - 3-е изд. стер. – М.: Высшая школа, 2005. – 495 с.
11. Кузнецов заданий по высшей математике. Типовые расчеты. – М.: «Высшая школа», 1994. – 207 с.
12. , , Кожевникова математика в упражнениях и задачах: Учеб. пособие для студентов втузов. В 2-х ч. – 4-е изд., испр. и доп. – М.: Высшая школа, 1986. – 304 с., 415 с.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 |




