ГИПЕРКОМПЛЕКСНОЕ ИСЧИСЛЕНИЕ В ЗАДАЧАХ ГЕОФИЗИКИ
©
Гипотеза Канта – Лапласа – Шмидта, согласно которой Солнечная система появилась из космического мусора, несостоятельна. Наука ХХ века не решила проблему шаровой молнии. Большой адронный коллайдер – будущий провал ненаучного субъективизма (мир – это то, что «варится в голове» Эйнштейна). Предложено альтернативное решение задач земного электромагнетизма. Солнце продолжает создавать свою планетную систему. Ядро Земли относительно холодное, полое. Шаровые молнии – следствие взаимодействия солнечного ветра с геомагнитным монополем, но не «черные дыры», которых не может быть в Единой Вселенной по определению.
Данные о строении Земли. Форма – геоид. Размеры: Rполюс ≈ 6356.78 км, Rэкват ≈ 6378.16 км. Орбита Земли вокруг Солнца: Rорб ≈ 150 млн. км. Возраст Земли: t ≈ 4.55 млрд. лет. Масса М = 5.98 ∙10 24 кг. В центре Земли давление Р ≈ 3.6 ∙ 10 6 Атм, температура T ~ 5000 o K.
|
|
|
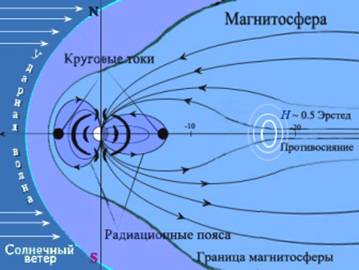
Рис. 1 Магнитосфера Земли деформирована Солнечным ветром [[1]] |
Земля заряжена отрицательно: q ≈ –5.7 ∙ 10 5 k. Напряженность электрического поля вблизи поверхности: Е ~ 125 В/м, в ионосфере ~ 250 кВ/м. Магнитное поле Земли (МПЗ) у полюса: Н ≈ 47.8 А/м, на экваторе: Н ≈ 19.9 А/м. Круговые токи, связанные с суточным вращением Земли, образуют магнитный диполь с южным полюсом вблизи (2100 км) географического Северного полюса. Вариации МПЗ по амплитуде: δB ≈ 10 – 7 Tl. Амплитуда магнитных бурь: 10 – 6 Tl. Отмечаются колебания МПЗ в пределах ΔВ ≈ 5 ∙ 10 – 7 ÷ 2.5 ∙ 10 – 5 Tl ([1]). Ионосферные токи: в полярных струях I ~ 2 ∙ 10 6 А; авроральные токи достигают 10 9 А. Магнитосфера Земли взаимодействует с солнечным ветром (рис. 1).
Солнечный ветер состоит из ионов и электронов (n ~ 100/см3). Скорость ионов вблизи Земли по оценкам С. Чепмена [[2]] лежит в пределах: 470 < ui < 1600 км/с. Скорость электронов зависит от механизмов разгона и близка к пределу: ue ~ c (даже при торможении в космическом магнитном поле КМП: 10 – 6 ≤ Н ≤ 10 – 4 Э) → электрический потенциал ![]() . Поэтому ионы поглощаются в основном ионосферой. Электроны достигают земной коры и магмы, заряжая их отрицательно (рис. 3). Вертикальный электрический ток: Iz ~ 10 – 6 μA/м2 при разнице потенциалов между ионосферными слоями большой проводимости (высота h ~ 50 км) и поверхностью земли до 6 мегаВ. Мощность 0.8 ÷ 1 гигаВт. В мире вспыхивает порядка 10 4 молний/с, в солнечную погоду – более 10 6 зарниц/с, световые эффекты сопровождаются радугой. Планета – это, таким образом, гигантская электродинамическая машина.
. Поэтому ионы поглощаются в основном ионосферой. Электроны достигают земной коры и магмы, заряжая их отрицательно (рис. 3). Вертикальный электрический ток: Iz ~ 10 – 6 μA/м2 при разнице потенциалов между ионосферными слоями большой проводимости (высота h ~ 50 км) и поверхностью земли до 6 мегаВ. Мощность 0.8 ÷ 1 гигаВт. В мире вспыхивает порядка 10 4 молний/с, в солнечную погоду – более 10 6 зарниц/с, световые эффекты сопровождаются радугой. Планета – это, таким образом, гигантская электродинамическая машина.
Векторный электрический потенциал. Для описания электромагнитных явлений исполь-зуется алгебра октав О (алгебра радуги, алгебра Кэли), вводится операторный терм [[3]]:
![]() = ∂/u∂t + i∂/∂x + j∂/∂y + k∂/∂z + αE
= ∂/u∂t + i∂/∂x + j∂/∂y + k∂/∂z + αE![]() + β(I∂/∂px + J∂/∂py + K∂/∂pz), (1)
+ β(I∂/∂px + J∂/∂py + K∂/∂pz), (1)
где u – характерная скорость взаимодействий (u = 1), α = m’/m2u3, β = m’ – константа размерности: [m’] = кг/с, m – масса источников поля, i ![]() O ≠ i
O ≠ i ![]() С. Предметный терм:
С. Предметный терм:
U = φ + iAx + jAy + kAz + Eψ + IBx + JBy + KBz, (2)
где φ – скалярный потенциал электрического поля, А – векторный потенциал магнитного поля, ψ – скалярный магнитный потенциал, В – векторный электрический потенциал.
Принимается «параллельная», или «экстремальная» схема приведения ([2]) алгебры (1, 2), построенной на сюръекции Θ | Е8 → f (E8), допускающая гомеоморфизм Ξ | f (Е8) ↔ E8:
![]() U = 0. (3)
U = 0. (3)
Результат приведения (3) отображается в 8-мерное пространство Евклида.
В системе уравнений, построенной по алгоритму (3), с условием на потенциал ψ ≡ 0:
∂φ/∂t – div A – βdivp B = 0,
∂A/∂t + rot A + grad φ + α![]() B – βrotp B = 0,
B – βrotp B = 0,
– div B + α![]() φ + βdivp A = 0, (4)
φ + βdivp A = 0, (4)
∂B/∂t – rot B – α![]() A – βrotp A + βgradp φ = 0,
A – βrotp A + βgradp φ = 0,
если α ~ 0, можно пренебречь слагаемыми с этим коэффициентом. При отсутствии явной зависимости потенциалов φ, А от импульса р из (4) исключаются их производные по координатам рх, ру, рz. Тогда система уравнений (4) приобретает вид:
∂φ/∂t – div A – m’divp B = 0,
∂A/∂t + rot A + grad φ – m’rotp B = 0,
div B = 0, (5)
∂B/∂t – rot B = 0.
В калибровке Кулона div A = 0 (а также при условии divp B = 0) определяются напряженности основных и дополнительных (с индексом В) полей (6) ([3]) :
|
H = rot A, |
HB = rot B, |
|
E = –∂A/∂t – grad φ, |
EB = – m’rotp B. |
Из (6) следуют уравнения Максвелла для полей, связанных с потенциалами φ, A:
div H = 0,
rot H = 4πj,
div E = 4πρ, (7)
rot E = – ∂H/∂t,
и система уравнений для дополнительных полей, определяемых потенциалом В:
div HВ = 0,
rot HВ = 4πjВ,
div EВ = 0, (8)
rot EВ = – ∂ЕВ/∂t,
где jВ – плотность тока магнитных мультимоментов (изменение намагниченности, линейной величины и ориентации, распределения в средах земной коры, магмы, ионосферы). Вместе со 2-м, интерес представляет 4-е уравнение системы (8): при определенных внешних условиях возможна вихревая локализация полей HВ, ЕВ. Подставляя во 2-е уравнение значение rot В = ∂В/∂t, получим ∂НВ/∂t = 4πμВ. Преобразуя 4-е уравнение в интегральную форму, придем к выражению для электрического воздействия в контуре С, охватывающем площадь S:
ξВ = –![]() ∫(EBn)dS,
∫(EBn)dS, ![]()
![]() (*)
(*)
что является дополнением к Э. Д.С., наводимой в контуре С согласно закону Фарадея:
ξ = – ![]() ∫(Нn)dS. (**)
∫(Нn)dS. (**)
В калибровке ∂φ/∂t – div A = 0, divp B = 0 для симметризованных определений:
|
H = rot A, |
HB = m’rotp B, |
|
E = –∂A/∂t – grad φ, |
EB = –∂B/∂t – m’rotp B, |
(9)
в условии |rot rot G| » |d2G/dt2| уравнения для Н, Е имеют вид:
div H = 0,
rot H = 4πj – ∂Е/∂t,
div E = 4πρ, (10)
rot E = – ∂H/∂t.
Для полей НВр, ЕВр получается система уравнений, тоже не зависящих от Н, Е:
divр HВр = 0,
rotр HВр = – m’ΔpB ≡ 4πm’μВр,
divр EВр = 0, (11)
rotр EВр = – 4πm’μВр – ∂HВр/m’∂t,
где μВр – плотность дополнительного магнитодинамического тока.
Вид системы (11) указывает на вихревую аномалию по полям HВр, ЕВр в отсутствие электрических и магнитных зарядов. Кроме того, обнаруживается еще один источник наведения Э. Д.С. в контуре С:
ξВр = – ![]() ∫(НBрn)dS. (***)
∫(НBрn)dS. (***)
Скалярный магнитный потенциал. Исследуем систему (3) в предположениях ψ ≠ 0, В ≡ 0, |rot rot G| >> |d2G/dt2| при тех же условиях по зависимости от импульсных координат:
∂φ/∂t – div A – α![]() ψ = 0,
ψ = 0,
∂A/∂t + rot A + grad φ – βgradp ψ = 0,
∂ψ/∂t + α![]() φ = 0, (12)
φ = 0, (12)
grad ψ – α![]() A = 0.
A = 0.
Положим α![]() = α
= α![]() Δ ≡ α’Δ, где h – аналог постоянной Планка, Δ – лапласиан, [α’] = м. В калибровке div A + α’Δψ = 0 определим напряженности полей Н, Е, Нψ, Еψ:
Δ ≡ α’Δ, где h – аналог постоянной Планка, Δ – лапласиан, [α’] = м. В калибровке div A + α’Δψ = 0 определим напряженности полей Н, Е, Нψ, Еψ:
|
H = rot A, |
Hψ = grad ψ, |
|
E = –∂A/∂t – grad φ, |
Eψ = m’gradp ψ. |
(13)
Систему (12) перепишем в виде:
∂φ/∂t – div A + 4πα’μψ = 0,
∂A/∂t + rot A + grad φ – m’gradp ψ = 0,
∂ψ/∂t – 4πα’ρ = 0, (14)
grad ψ + 4πα’j = 0,
где μψ = –Δψ/4π – плотность магнитного заряда mψ.
Система уравнений для полей Н, Е имеет вид:
div H = 0,
rot H = 4πj + 4πα’grad μψ,
div E = 4πρ – 4πα’∂μψ/∂t, (15)
rot E = – ∂H/∂t.
Система уравнений для полей Hψ, Еψ записывается следующим образом:
div Hψ = – 4πμψ,
rot Hψ = 0,
div Eψ = – div E,
rot Eψ = – rot E + 4πj + 4πα’grad μψ , (16)
divр Eψ = – 4πm’μψp,
rotр Eψ = 0,
где μψp – плотность динамического магнитного заряда. При grad μψ > 0 на дневной поверх-ности и μψ < 0 уравнение 4 в (16) дает гармонический (см. ниже) вклад в Э. Д.С. контура С.
Из 4-го уравнения в (14) следует: div grad ψ ≡ Δψ = – 4πα’div j = – 4πμψ, μψ = α’div j. Если электрический заряд сохраняется: div j + ∂ρ/∂t = 0, то μψ = – α’∂ρ/∂t. Из 3-го уравнения в (14) получаем: ∂2ψ/∂t2 = 4πα’∂ρ/∂t = – 4πμψ, или, в итоге, уравнение Даламбера для ψ:
Δψ – ∂2ψ/u2∂t2 = 0, (17)
т. е. волны ψ существуют вне области распределенного заряда mψ.
Общее решение задачи Коши для уравнения (17) в сферически симметричном случае строится на основе частного решения Ψ(t, r) = μо[δ(r – ut) – δ(r + ut)]/4πur, где δ(r) – δ‑функция Дирака, полученного при начальных условиях Ψо = 0, ∂Ψо/∂t = δ(r) = δ(r)μо/2πr2. В «точке» r = 0 – особенность. Решение уравнения (17) при ψ|t = 0 = ψo, ∂ψ/∂t|t = 0 = Ωψo есть
ψ(t, r) = ψo∫ V’ (ΩΨ + ∂Ψ/∂t)dV’, (18)
где Ψ = Ψ(t, |r – r’|), [ψo] = c/м3, V’ – область с μψ. Опережающие решения отвечают удален-ным на ∞ источникам поля. Использование потенциала ψ допускает нарушение 2-го начала термодинамики [[4]] (магнитная активность Солнца, сверхсветовой солнечный ветер, КМП).
Из 2-го уравнения в (15) следует: div j = – α’Δμψ. Поскольку α’div j = μψ, уравнение для плотности μψ принимает вид однородного уравнения Гельмгольца:
Δμψ + (2π/λ) 2μψ = 0, (19)
λ = 2πα’. Решение (19) под сферой СФ радиуса RФ с условием μψ |СФ = 0 или ∂μψ/∂n |СФ = 0:
μψ(r) = ![]() ∫ СФ[(eikR/R)(∂μψ(r’)/∂r’) – μψ(r’)(∂/∂r’)(eikR/R)]dS’, (20)
∫ СФ[(eikR/R)(∂μψ(r’)/∂r’) – μψ(r’)(∂/∂r’)(eikR/R)]dS’, (20)
где R = |r’ – r|. Вне шара Ф: μψ = 0 [[5]], ψ ≠ 0. Уравнение (19) имеет набор фундаментальных решений для дискретных значений момента (α’ = m’r2v2/2mu3, где rv = ζrovo, ζ из R) и описывает стоячие волны плотности μψ в Ф: μψ = μψ0Re( ∑ ζ ≥ 0 eikζr)/r, μψ0 = Re(аψe–iωζt), kζ = ![]() /α’(ζ),
/α’(ζ), ![]() = n – inim, nim > 0, и амплитуда волн от центра убывает [[6]]. Коэффициент поглощения: nim ~ (ωμ)1/2. При их числе N » 1, все компоненты grad μψ(kn) ортогональны (dim V » 1).
= n – inim, nim > 0, и амплитуда волн от центра убывает [[6]]. Коэффициент поглощения: nim ~ (ωμ)1/2. При их числе N » 1, все компоненты grad μψ(kn) ортогональны (dim V » 1).
При условиях (13) плотность заряда ρ является источником “подогрева” μψ:
Δμψ – 4πσ∂μψ/∂t = – 4πσρ/α’. (21)
Учитывая решения уравнений (17, 19), граничные условия для (21) достаточно принять в виде: μψ |СФ = 0, ∂μψ/∂n |СФ = 0 [5]. От знака ρ зависит направление процесса (nψ > 0 для +ρ).
В случае μψ-«электрона», т. е. при h = ħ/2 и массе m = mе, коэффициент α’ ≈ 0.273 мм = λ’ → ν’ ≈ 1.098 тГц. Введем ε(μψ) как набор осцилляторов εn = ħω(n + СS’/2 + 2) в поле U = 2π∫Ф ρMω2r4dr ≈ mω2r2/2 шара Ф [[7]]. Здесь СS ≈ 2 4s ≡ j – число степеней свободы в гиперкэлеровом пространстве s монополей V4s, определяемое факторизацией [[8]] (при диффеоморфизме Θ | f(Е4k) → E4k) пространства V4s по подгруппам группы SO(4s). Если s = 1 и калибровка фиксирована, то фазовая окружность S1 не рассматривается, и СS’ = 3. При тепловом равновесии одного несвязанного монополя (![]() ) с реликтовым излучением ([4]): εn = εт = 13kT/2 = ħωrel, где Т ≈ 2.7 К – температура реликтовых частиц, имеющих 9 степеней свободы движения, колебаний, вращения, 3 спина и 1 заряда. Длина реликтовой волны λrel ≈ 0.13 мм (реальная длина волны реликтов на максимуме интенсивности λ ≈ 0.11 мм).
) с реликтовым излучением ([4]): εn = εт = 13kT/2 = ħωrel, где Т ≈ 2.7 К – температура реликтовых частиц, имеющих 9 степеней свободы движения, колебаний, вращения, 3 спина и 1 заряда. Длина реликтовой волны λrel ≈ 0.13 мм (реальная длина волны реликтов на максимуме интенсивности λ ≈ 0.11 мм).
|
|
|
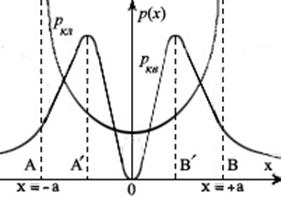
Рис. 2 Сравнение квантовой вероятности местонахожде- ния частицы ркв для n = 1 c классической ркл. А, В – точки поворота, А’, B’ – точки максимума ркв |
В квантовом приближении: ε = ∑ n ≥ 0 рnεn = εт, где рn – коэффициенты, ∑ n ≥ 0 рn = 1, или вероятности состояний n: рn = |χn|2 ~ exp(– r2/α’2)r2n/α’2n+1, где χn – волновые функции, рис. 2, [[9]]. Вероятность перехода из нулевого состоя-ния εо → εk: pok = κke– κ/k!, κ = F 2/16meħπ3ν3 – параметр распределения Пуассона, F = q2/α’2 – воздействие (электрического) поля Е ≈ const. Осциллятор является возмущением среды, поэтому ħkrel = ħkn(εμ)1/2. В табл. 1 даны оценки произведения проницаемостей εμ для различных слоев плотности μψ ([5]), см. [[10]]. Для s притягивающих друг друга отрицательных монополей j » 1, и ν ~ εμ ~ uгруп ~ M ~ 0. Если ε ~ 1, то μ ~ 0.
|
n |
0 |
1 |
2 |
3 |
|
ω / 1011, c–1 |
6.5616 |
5.1034 |
4.1755 |
3.5331 |
|
λ ∙ 10 4 / 2π, м |
4.5689 |
5.8744 |
7.7979 |
8.4852 |
|
εμ |
0.0816 |
0.0499 |
0.0331 |
0.0236 |
|
uгруп / 108, км/с |
0.8565 |
0.6621 |
0.5451 |
0.4612 |
|
ρM ∙ 1021, кг/м3 |
4.188 |
8.8667 |
16.189 |
26.772 |
|
М, кг |
0.0313 |
0.0666 |
0.1216 |
0.2008 |
Оценим ε в плазме под СФ. Если заряд +Qp ядра сосредоточен в оболочке (свободные протоны) и плотность электронов мала в сравнении с плотностью элементарных монополей, то под СФ вдали от резонансов (ωр, ωе, ωμ > ω) диэлектрическая проницаемость для n-гармоники в d-слое независимо от значения магнитной проницаемости (см. [[11]]): εn ≈ 1 + 4πм2μψn/[(ωψn2 – ω2)Mψn, где м – элементарный заряд монополя, μψn – плотность монополей, Mψn – масса магнитного заряда в состоянии n, ωψn – собственная частота осциллирующего монополя (~1011 Гц). В условиях синфазности в любом слое стоячих волн (см. ниже) плотности μψn и массы Mψn их отношение конечно, и εn > 1. Из оценок в таблице следует: проницаемость μ « 1. То есть ядро с магнитным зарядом является сильным диамагнетиком, и магнитное поле «выталкивается из него» (эффект Мейсснера), как из сверхпроводника температуры Т < Ткрит. Это согласуется с отсутствием волн ψ там, где распределен магнитный заряд (← уравнения (17, 19)), и используется при выводе других уравнений.
Z Сейсмическое зондирование обнаруживает ядро радиуса Rядро ~ 1215 км = α’; его жесткость ς = Mω’2. Плотность оболочки ρС ≈ 13 г/см3, толщина 10 км [[12]]. Скорость электронов uе ~ 1000 км/с, концентрация ρе ≈ 2.286 ∙ 1015/м3, электрическое поле Ее ~ 3.518 ∙ 10 6 В/м, проводимость σе ~ 6.449 ∙ 10 14 / Ом ∙ м ([6]) (больше σСu примерно в 107 раз). В приближении εμ ≈ 1, частоты обращения ψ‑волн вокруг ядра ν’ ≈ 40 Гц, электронов в слое СФ примерно 0.13 Гц.
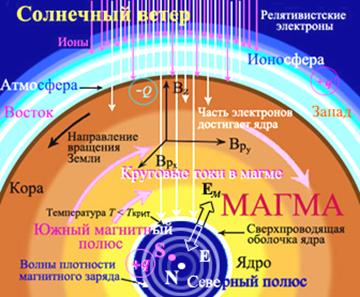
Упругие волны плотности вещества отражаются от ядра, внутрь не проникая. Плотность массы под СФ: ρM ≈ m’ν’2/8π(εμ)3/2u3 (см. табл. 1). Но ряд по уровням ε ограничен распределением Пуассона и зависимостью ε = ε(ω) внутри ядра. Таким образом, в центре Земли расположена практически пустая область размера ~ 2α’. Масса ее слоев М меняется вследствие переходов μψ-субстанции между уровнями εn. Жесткость ядра невелика – значения 1 < ς < 100 не для твердого никеля или железа. В связи с переходами n ↔ k шар Ф пульсирует по массе. Классический электромагнетизм в Ф исчезает, т. к. поле Н вытолкнуто из полости ([7]). Если в ядре (рис. 3) Нψ ≈ 0, то grad ρ ≈ 0, и получаем уравнение “теплопроводности” (при μ = 1 ср. со скин-эффектом [4]) для поля Е (R3 \ Ф ↔ Ф \ СФ):
ΔЕ – 4πα’(σ/χ)∂E/∂t = 0, (22)
где χ – электроемкость (слоя СФ). Принято j = σE. При выводе (22) использовались: уравнение j = – α’grad μψ, полученное из 2-го уравнения в (15), 3-е и 4-е уравнения (15) и условие σ ≈ const. В шаре ΔЕ ≈ 0. Рассмотрим приближение полупространства. Начало цилиндрических координат на нижней сфере слоя СФ, направление оси Z в R3 \ Ф. Тогда индукция Е ≈ Еое –z/δei(z/δ – ωt), где δ ≈ u(2πσω/χ) –1/2 = (2u2α’2/σω)1/3. Для Еψ в шаре ΔЕψ ≈ 0 и в слое приближение: Еψ = –Еое– z/δei(z/δ – ωt). Сейсмические оценки толщины сверхпроводящего слоя дают значение δС ≈ 10 км, и микро-, телеволны через СФ не проникают (не из-за магмы). Значение Е во времени уменьшается, если нет подпитки внешним полем (электронами Черенкова).
Групповая скорость под СФ вдали от резонанса (ωψ > ω) определяется формулой:
uC = u(εμ)1/2 = uμ1/2[1 + 4πм2μψ/[(ωψ2 – ω2)Mψ]1/2, (23)
|
|
|
Рис. 3 Схематический разрез Земли. Распределение электрических за- рядов напоминает модель атома: в центре положительно заря- женное ядро, кора – электронная оболочка, ионосфера – наве- денные заряды. Полюса S, N и система координат для магнит- ной индукции помещены на воображаемой сфере над корой |
uC ~ μ1/2 → 0, и частицы, «втягиваемые» зарядом mψ = ∫μψdV в разреженную холодную плазму, перед исчезновением становятся мощными источниками излучения Черенкова.
Масса земного ядра мала: М ≈ 4/3 πα’3ρM, момент вращения невелик: h ≈ 4/5 πα’5ρMω’ при ρM ≈ сonst.
В обычной среде метрика r = |r – r’| определяется посредством эле-ктромагнитных волн, распространяю-щихся со скоростью u. Введем метрику в среде С: rС = М|r – r’|, где число Маха М = u/uгр, u – скорость вне С, uгр – групповая скорость в С, (tC = Mt). Для полости Ф, хранящей информацию о ранних стадиях Метагалактики([8]), примем М = (εμ)– 1/2. Пусть ядро состоит из двух фаз: протонного газа Фр и монополей Фμ. В ядре число М » 1, что означает: эффективный показатель адиабаты Пуассона γ ≈ 1, коэффициент плотности протонной фазы ξ = (γ – 1)/(γ + 1) ≈ 0, и предполагаемая фаза монополей становится истинной. Так как количество степеней свободы всех движений монополей j → ∞, где j = 2/(γ – 1), то dim V → ∞, где V = V4k/SO(4k) × Vp × R3. Чем интенсивней приток протонов в Ф, тем больше М и сильнее компактифицируется ядро при массе и радиусе М ≈ α’ ≈ const. Иначе говоря, атомы из протонов и элементарных монополей «исчезают» в дополнительных измерениях V4k/SO(4k).
|
|
|
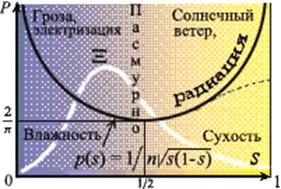
Рис. 4 Распределение частоты θ появления шаровых молний в грозу, пасмурные и солнечные дни |
Потенциалы φ, ψ, В. Опытные данные [[13]] показывают, что моды выборки (n ~ 1000) по цвету, размеру, времени жизни шаровых молний (SM) лежат в пределах: λжелт ≤ λ ≤ λкрасн, 15 ≤ Ø ≤ 30 см, 10 ≤ τ ≤ 50 с. Частоты вариационных рядов niζ по значениям многих признаков ζ аппроксимируются распределениями: Бернулли с малой вероятностью р события ξ+, логарифмически нормальным с параметром 0 + ε < σ < 1, χ-квадрат c степенями свободы 3 ≤ n ≤ 13, положительным устойчивым законом с параметром σ = ½. Отмечается корреляция Ø и τ. Появление молний зависит от погоды по другому закону [[14]]. На рис. 4 приведенная влажность g = 1 – s. Фактический ряд значений θ при s ≈ ¾ начинает терять частоту (пунктир). Сравнение с типичными графиками p(ζ) вида Ξ приводит к выводу: линейные молнии в условиях повышенной электризации пространства и влажности воздуха являются катализаторами SМ – основная причина их появления лежит во взаимодействии солнечного ветра (поток электронов Черенкова) с магнитным зарядом ядра Земли. Коэффициент корреляции r(Ø, τ) ~ 1 приводит к предположению: SM‑долгожители содержат относительно большой заряд mψ, и область под их высокопроводящей оболочкой компактифицирована. Перечисленные факты являются причиной введения скалярного магнитного потенциала ψ совместно с векторным электрическим потенциалом В (в пренебрежении влиянием векторного магнитного поля Земли А = 0, связанного с токами в магме и ионосфере).
Система (3) с оператором α![]() = – α’Δ + αU, где U – потенциальная функция, если потенциалы явно не зависят от импульса р, в приближении ΔΘ = – 4πθ принимает вид:
= – α’Δ + αU, где U – потенциальная функция, если потенциалы явно не зависят от импульса р, в приближении ΔΘ = – 4πθ принимает вид:
∂φ/∂t – 4πα’μψ – αUψ = 0,
grad φ + 4πα’jB + αUB = 0,
∂ψ/∂t – div B + 4πα’ρ + αUφ = 0, (24)
∂B/∂t – rot B + grad ψ = 0.
Определим поля при условии div B + (α’Δ – αU)φ = 0 в “классической форме” ([9]):
|
Н = rot A, |
НВ = rot B, |
|
Е = – grad φ, |
Еψ = – grad ψ – ∂B/∂t. |
(25)
Тогда система уравнений для полей Н, Е имеет следующий вид:
div H = 0, rot H = 0,
div E = 4πρ, rot E = 0, (26)
и для полей НВ, Еψ, используя 1-е и 2-е уравнения в (24), получаем:
div HВ = 0,
rot HВ = 4π(1 – αα’U)jB + 4πα’grad ρ + αφ grad U – α2U 2В,
div Eψ = 4π(1 – αα’U)μψ – 4πα’∂ρ/∂t – α2U2ψ, (27)
rot Eψ = – ∂HВ/∂t,
В случае U ![]() ψ для области без момента (α’ = 0) из 3-го уравнения (24), с привлечением уравнений 1 и 4, получается нелинейное интегро-дифференциальное уравнение:
ψ для области без момента (α’ = 0) из 3-го уравнения (24), с привлечением уравнений 1 и 4, получается нелинейное интегро-дифференциальное уравнение:
–Δψ = ∂2ψ/∂t2 + ![]() (∫ψ2dt) ∂ψ/∂t +
(∫ψ2dt) ∂ψ/∂t + ![]() ψ3, (28)
ψ3, (28)
где ![]() = αl, l – константa размерности ([10]). В области с моментом (α’ > 0) и U ≈ 0 из 1-го уравнения системы (24), используя 3 и 4 уравнения, для плотности μψ находим:
= αl, l – константa размерности ([10]). В области с моментом (α’ > 0) и U ≈ 0 из 1-го уравнения системы (24), используя 3 и 4 уравнения, для плотности μψ находим:
Δμψ – (2π/λ’) 2μψ = 0, (29)
|
|
|
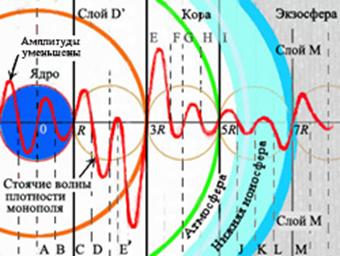
Рис. 5 Стоячие волны плотности магнитного заряда μψ ядра ♀. Слой D, пучность Е’ внутри внешнего ядра под слоем D’, обнаруженного сейсмозондированием. Слои F, G, H в магме. Узлы: I – дрейф μψ на коре; J, K, L, M – в ионосфере. Декремент амплитуды суперпозиции первых 4-х гармоник снижен для наглядности изображения. |
где λ’ = 2πα’. Физически приемлемое решение (см. квантовые вероятности местонахождения частиц и [7]): μψ = μψоехр(–r/α’)/r ∑ n ≥ 0 ansin(2πnu~t/λ’n + αn) описывает волны вне Ф, затухающие на периферии. Под СФ: μψ = μψо/r ∑ n ≥ 0 bnsin(2πnr/λ’n + βn)∙∑ n ≥ 0 cnsin(2πnut/λ’n + γn). Условие сшивки решений: μψ(u) | r = α’– δC + μ~(uC) = μψ(u~) | r = α’, где u, uC, u~ – магнитогидродинамические скорости под СФ, в СФ, вне Ф. Большие частоты подавлены. В приближении равенства амплитуд, мощный узел первых 4-х резонансных волн с сильным потоком плотности μψ, концентрацией волн ψ и прозрачностью слоя СФ, обратно пропорциональной (σω)1/2, – примерно на расстоянии 3α’. Это критический слой D’ [12], в котором поперечные волны сs гаснут. Слоистая структура магмы является, в том числе, следствием влияния волн плотности μψ. На дневной поверхности – всплеск гармонических колебаний скорости элементов μψ и над нею 11-я пучность на высоте ~ 300 км (рис.5; R = α’). Для резонанса с λ ~ α’/6 пучность на высоте 50 км (ионосферный слой высокой проводимости). Заметен всплеск подвижности μψ в слое М экзосферы ([11]). В пучностях вероятность индукции отдельного магнитного заряда mψ из его плотности μψ повышается: р ~ Hψ2/|mψ| > 0. Это косвенно указывает на связь появления шаровых молний вблизи дневной поверхности с магнитным зарядом ядра Земли.
В терминологии [[15]] монополь mψ (активатор) является «горячим», а его потенциал ψ и поле Нψ (носитель) «холодными» автосолитонами АС (процессы диффузионного типа с подпиткой). Распределение ингибитора показывает, что ядро излучает. Устойчивость структуре АС придает также гравитационное поле. Диффузия солитона ψ, описываемого уравнением (28), возможна в магме, но это дополнительная теория. Волны ψ вероятны на дневной поверхности, т. е. в узле μψ, где давление магнитных волн относительно большое. Для описания аномальных процессов в атмосфере используется система (27) с потенциальной функции U ![]() φ + B.
φ + B.
Z Если поле Нψ = –grad ψ – ∂В/∂t и ЕВ = rot B (суть системы (27) не меняется), то элементарный анализ показывает, что вектор Нψ отрицательного заряда mψ (при малости суточных изменений ∂В/∂t) направлен вниз и убывает с высотой – ток протонов правой спиральности к оси Z и усиливается с набором высоты, уменьшает Нψ. Электроны Черенкова создают вертикальный ток вверх и “магнитное поле” ЕВ правой спиральности, что уменьшает ток jB за счет прецессии +q вокруг ЕВ. В итоге блоки крупных молекул с насыщенным облаком общих электронов, взаимодействуя с полем Нψ в условиях гравитационного притяжения, с крейсерской скоростью vrot устремляются вдоль силовых линий поля ЕВ, образуя левоспиральные структуры. Не только молекулы ДНК имеют левую спиральность, но и другие цепочки из сложных молекул, отвечающие долгосрочной магнитной погоде Земли на протяжении миллиардов лет. Монополь +|mψ| в центре планеты индуцирует правый вариант органической жизни.
Другой эффект связан с авто-диамагнетизмом в “калибровке” div B = 0. Элемент μψ испытывает радиальные колебания между сферическими пучностями с максимальной скоростью в узле Ud вдоль поля Нψ = –grad ψ вне сферы Сd. Под Сd поля Нψ нет, что эквивалентно значению μ ≈ 0. Если плотность стоячих волн магнитного заряда представлена в виде ряда: μψ = ∑ansin(ωnt)sin(knr), то закон сохранения div jB + ∂μψ/∂t = 0 и значение jB = vμψ, где v – радиальная скорость μψ, для плотности магнитного тока дают в узле: vn = (ωn/2kn)ctg(ωnt)ctg(knr). Т. к. в нем два потока μψ со стороны двух полуволн (рис. 6), создается гармонический ток jВn = аn(ωn/kn)cos(ωnt)cos(knr) и вихревое поле rot ![]() . Ток плотности μψ сдвинут по фазе на π/2 и направлен вверх, и прецессия вокруг линий
. Ток плотности μψ сдвинут по фазе на π/2 и направлен вверх, и прецессия вокруг линий ![]() соседних элементов μψ «диамагнитно» уменьшает jВn. В сферическом узле Ud переменный ток монополей IВd ≈ 4πRd2δdjВ, где δd – толщина слоя d, в среднем равен нулю и по периоду, и по δd. Поля, создаваемые этим током на расстоянии r > Rd, малы. Вне стоячих волн в Ф \ СФ поля слоев Сd определяются по энергетическому воздействию (среднеквадратическое значение mψ, Нψ,
соседних элементов μψ «диамагнитно» уменьшает jВn. В сферическом узле Ud переменный ток монополей IВd ≈ 4πRd2δdjВ, где δd – толщина слоя d, в среднем равен нулю и по периоду, и по δd. Поля, создаваемые этим током на расстоянии r > Rd, малы. Вне стоячих волн в Ф \ СФ поля слоев Сd определяются по энергетическому воздействию (среднеквадратическое значение mψ, Нψ, ![]() ). Отрицательные значения плотности: μψ < 0 и массы: мψ < 0 обусловлены поперечными колебаниями монополя на упругой «границе» физического мира с его отражением в вакууме (с его преформой в эфирном состоянии материи).
). Отрицательные значения плотности: μψ < 0 и массы: мψ < 0 обусловлены поперечными колебаниями монополя на упругой «границе» физического мира с его отражением в вакууме (с его преформой в эфирном состоянии материи).
Факты и гипотезы. А) Индукция ядром Земли шаровых молний вблизи дневной поверхности при соответствующих физических условиях. Часть НЛО как шаровая молния, переносимая ветром по эквипотенциальным поверхностям над землей. Эти НЛО не созданы кем-либо, а объективное явление физического мира ([12]), в т. ч. влияние параллельных миров (ПМ).
B) Потенциал мозга меняется в пределах: – 108 < U < + 6 ∙ 107 B, его частота: α ≈ 8 ÷ 13 Гц и стоячая α-волна вокруг земного шара с λ ≈ (3 ÷ 4) ∙ 107 м – конформное отображение (размеры головы а ≈ 15 ÷ 20 см) → размеры молекул ρ ≈ 5 ÷ 10 Ǻ. Характерна пропорция: Rэкват/α’ = a/2b, где b – радиус свода зрительного бугра, куда поступает свыше 90% информации из внешней среды. Полость «земля–ионосфера» – это резонатор частот 8, 14, 20 – 32 Гц, включающих β‑частоту мозга 14 ≤ β ≤ 33 Гц. Частота 400 ≤ Ω ≤ 1000 Гц электрических импульсов между нейронами – конформное отображение → волны в ядре: 300 ≤ λ ≤ 750 км < α’. Собственная частота ядра Земли: ν’ ≈ 40 Гц ↔ Ω и возможность упаковки информации о жизнедеятельности человека в СФ U Ф на фазе сверхсильного диамагнетика пространства s монополей V4s размерности СS ≈ 2 4s » 1, на протонной фазе размерности d » 1 и в пространстве R3 с метрикой rМ = Мr вместимости М3 » 1 при обычных скоростях движения v ≈ dr/dt.
С) В структурах мозга (жидкие кристаллы коры и ликвора), ввиду проницаемости его нейронной среды, отвечающей гиперкомплексному моделированию свойств биоткани, возможны состояния, влияющие на распространение электромагнитного излучения: групповая скорость сигнала больше его фазовой скорости. Следовательно, вполне вероятна сверхсветовая скорость обмена информацией мозга не только в 3-мерном мире, но и по другим измерениям. В том числе возможна связь с 3-расслоениями физического пространства в 4-мире, с так наз. параллельными мирами, а именно: через четвертое и другие измерения ∞-мерного мирового пространства. С другой стороны, скорость света конечна лишь потому, что в физическом мире существуют бóльшие скорости. В природе нет запрета на скорости u > c. Возможен вход в ПМ на микро - и макроуровне.
Z D) Возможность индукции на дневной поверхности информационных копий человека по хранящейся в Ф информации – на полевых носителях малой энергетики. При спонтанном взаимодействии с ядром на низких частотах и вынужденном (волевом) переходе биополя человека (ауры) в состояние активатора – возможность телепатии и левитации. Действительно, передача телепатемы осуществляется в 4 этапа: сознание индуктора → его подсознание (ядро) → подсознание перципиента (ядро) → его сознание; в воде телепатема гаснет и интенсивность ее падает с расстоянием как 1/r2; способность к перцепции максимальна на частотах α-ритма [[16]]. Факты говорят о том, что ядро усиливает волновой пакет телепатемы. Эффекты ясновидения, совместимые с резонансом дециметровых волн в пространстве, ограниченном зеркалами, с подпиткой пламенем углеводородной (стеариновой, парафиновой) свечи, также основаны на электромагнитном взаимодействии организма с ядром Земли. Эффекты ясновидения и проскопии – ПМ и топология провремени.
E) Пакеты электромагнитных волн и поле ψ, модулированные информацией о конкретном homo sapiens, ядром Земли периодически излучаются в Космос (и поглощаются системами, подобными СФ U Ф). Жизнь во Вселенной возникает, распространяется и вечна независимо от сверхъестественных сил. Излучение планетой информационных пакетов так же естественно, как и тепловое движение молекул. Синтез гилозоизма, пантеизма и самодостаточности жизни.
F) Разумная жизнь на Марсе – на глубине до тысячи км и старше земной ~ на 1 млрд. лет. Тепло из недр, питание от Солнца напрямую – через хлорофилл кожи, продолжительность жизни марсианина ~ 100 000 лет, полеты в Космосе по иным измерениям. Колонии марсиан в недрах Луны, Земли, Венеры… Отношение марсианина к человечеству >> отношения человека к лесному муравейнику. В ядрах некоторых планет – высокоразвитые цивилизации.
G) Решение уравнения df(U)/dz = 0 для функционала f(U) = a0 + ∑∞k=1 akUk в области О Í Q, где k Î N, ak, a0, U в Q, Q – обобщенно неассоциативная некоммутативная алгебра, указывает на существование неисчислимого множества физических вселенных, основной закон движения в которых определяется обобщенным принципом экстремального действия. Действительно, в форме df(U)/dz = ∑∞q=1∑q-1p=0 aqUq-1-p(d/dz![]() U)Up = 0 содержится уравнений больше, чем в самом большом бесконечном множестве ассоциативной и коммутативной теории множеств Кантора (построенной на основной теореме школьной арифметики). Отсюда, если аq произвольны и U ¹ 0, следует, в частности, уравнение d/dz
U)Up = 0 содержится уравнений больше, чем в самом большом бесконечном множестве ассоциативной и коммутативной теории множеств Кантора (построенной на основной теореме школьной арифметики). Отсюда, если аq произвольны и U ¹ 0, следует, в частности, уравнение d/dz ![]() U = 0 для нашего мира октав и радуги. Здесь оператор d/dz ≡ ∑7n=0 jn d/dzn. Все эти вселенные – суть параллельные миры в гиперкомплексном аспекте.
U = 0 для нашего мира октав и радуги. Здесь оператор d/dz ≡ ∑7n=0 jn d/dzn. Все эти вселенные – суть параллельные миры в гиперкомплексном аспекте.
Н) Вывод о существовании неисчислимого множества физических вселенных равносилен выводу о самоограниченности численных методов вообще и геометрических методов в частности (вырождение физической картины мира по f(U) неустранимо в рамках количественных подходов). Наш 3-мерный мир является наиболее простым из миров, допускающим самоорганизацию достаточно емкой биологической жизни (ср. с известной задачей 4-х красок на плоскости). Для различных типов движения их числа степеней свободы в n-пространствах Евклида совпадают с коэффициентами разложения бинома Ньютона (а + b)n в полином – это числа сочетаний. И только в 3-мире число степеней свободы поступательного движения равно числу степеней свободы вращательного движения в плоскости. В нашем мире есть еще вращение пространства в целом, или 3-мерная воронка. Для потенциала Ψ получены решения уравнения (28) в виде продольных сферических волн и кольцевых поперечных волн в сферах. В 4-пространстве плоских вращений уже 6, а 3-мерных воронок – 4 типа.
Биота, возникшая в 3-мире, – лишь слабая тень свойств неисчерпаемой Вселенной.
[1] В геофизике используют величину 1γ = 10 – 5 Гс.
[2] Согласно методу . Эти уравнения гиперсимметричны, асимметрия вносится начальными и краевыми условиями конкретной задачи. Для сравнения: математическая база СТО – пространство Минковского.
[3] Переобозначено: B → H, D → E; диэлектрическая ε и магнитная μ проницаемости среды не рассматриваются.
[4] Возраст Земли исчисляется по ее твердой фазе с момента отпочкования от Солнца. Звезда возникает в результате конденсации материи на скоплении зарядов mψ, образовавшихся в эпоху Т о К = Треликт. Температурная память mψ обусловлена степенями свободы СS, а также изоляцией оболочки Сψ из захваченных электрических зарядов. Внутри звезды монополи μψ с моментом Μψ появляются из вакуума и периодически выталкиваются наружу под действием сил Архимеда и центробежной. Если свободные заряды одного знака μψ < 0 притягиваются и масса mψ < 0, то гравитационное взаимодействие атомов А{p, μψ} определяется массой протона mр > 0.
Для упрощения алгоритма оценок далее также принято: r → x; h(ςν) = ς(hν), т. е. уменьшение частоты эквивалентно увеличению числа частиц, и скопления μψ слоями ложатся под уровень «реликтового» фона.
[5] Если среда внутри СФ не поглощающая, то можно заменить ωC → (εμ)1/2 ωC, Hψ → (μ)1/2Hψ, где ε, μ – диэлектрическая и магнитная проницаемости в шаре Ф. Для групповой скорости u = α’νC → (εμ)1/2α’νC = uC.
[6] Проводимость СФ: σе ≈ ueρe/Ee, где ue ≈ (13kT/mе)1/2, Ee ≈ (52πkTρC/me)1/2.
[7] Отметим: в квант. физике и СТО использована единица кручения i![]() C → exp(iz) ← Дж. Непер, Л. Эйлер.
C → exp(iz) ← Дж. Непер, Л. Эйлер.
[8] В Единой Вселенной любой объект содержит информацию о ранних стадиях ее развития. Разрывать физический мир на несвязанные между собой «черные дыры», или связанные только в одном направлении передачи взаимодействия, – это вариант синтеза гегельянской и картезианской метафизики. Такой подход является атавизмом мышления, выработанного в эпоху диктаторских режимов, предшествующих современному миру, с их лозунгом «разделяй и властвуй». В целом информационно более бедная, нежели Биота или цивилизация, наука «богом избранных» произвела в 1905 – 1915 годах затяжной выкидыш: релятивистский предвестник общественно-политических событий 1917 года – субъективную теорию относительности и ее «черные дыры». То есть лозунг ростовщиков и менял-перекупщиков «твое – это мое» был загодя трансформирован в революсьённый псевдонаучный клич «всё относительно». Им казалось, что легче внушить свое превосходство сначала в науке, а лишь затем – в политике и экономике. На такой безнравственной базе «наука», собравшая вокруг Большого адронного коллайдера тысячи несамостоятельных научных работников, потерпит неизбежное фиаско. Так как мнение большинства в науке сейчас доминирует, то провал затеи БАК будет означать, в том числе, что Природа вокруг нас – живая, что планета Земля – не косное и бездушное нечто, а способна защищаться от зомби.
[9] Можно определить и поле Нψ, но сейчас интерес представляет соотношение μψ и ψ.
[10] Для сравнения: нелинейное уравнение Шредингера –ψхх = iψt + |ψ2|ψ имеет солитонные решения.
[11] Магнитогидродинамические эффекты и дисперсия в среде не учитываются (для магнитозвуковой стоячей волны плотности μψ). Выводы справедливы в корректных приближениях, принятых для упрощения расчетов.
[12] Представители официальной науки избегают проблем, суть которых им не понятна, не сулит материальной выгоды и общественно-социальных привилегий. Напротив, загадочные, аномальные явления отбрасываются методом обструкции исследователей, изучающих всё экстраординарное. Рьяно защищая свои лженаучные бастионы, «респектабельные» ученые проявляют, как правило, агрессию в отношении инакомыслящих, к теориям и экспериментальным результатам, представляющим угрозу для их положения сверху. Так наука, утеряв античную чистоту и непорочность, постепенно превратилась в стяжательское предприятие «элитных» сообществ, в свою противоположность. Вспомним «деятельность» Альберта Гора (США), из корысти методом фальсификации раздувающего проблему всемирного потепления. Между тем еще Платон предвидел это перерождение, назвав сборище незнаек в своей школе академией, самих слушателей академиками – от имени Академ. Так звали умалишенного бомжа, бесцельно бродившего по лесистым горным склонам Эллады. Современный Академ – Гор в 90-х годах безрезультатно бродил вокруг золотоносных гор Киргизии…
[1]. Солнечная и солнечно-земная физика / Под ред. А. Бруцека, Ш. Дюрана. – М.: Мир, 1980.
[2]. / Геофизика. – М.: Мир, 1964. С. 278 – 295.
[3]. Верещагин электродинамика / Фундаментальные проблемы естествознания и техники. Труды Всемирного Конгресса. Т. 1. – С-Петербург: Изд. СПбГУ, 2002. С. 30.
[4]. , Рыбаков . – М.: ВШ, 1990. С. 114, 126 – 126, 161.
[5]. Владимиров математической физики. – М.: Наука, 1981. С. 440, 49.
[6]. Кудрявцев поля и ее применение в геофизике. – Л.: Недра, 1988. С. 210 – 213, 205.
[7]. , Лифшиц механика. – М.: Наука, 1989. С. 93, 141, 143.
[8]. Atiyah M., Hitchin N. The geometry and dynamics of magnetic monopoles. – Princeton: University Press, 1988.
[9]. Блохинцев квантовой механики. – М.: ВШ, 1963. С. 178.
[10]. , Лифшиц сплошных сред. – М.: ГИТТЛ, 1957. С. 368, 250.
[11]. Волны / Берклеевский курс физики. Т. III. – М.: Наука, 1974. С. 498.
[12]. , , Цибаров моделирование в глобальных проблемах естествознания. – Новосибирск: Изд. СО РАН, 2005. С. 116 – 137.
[13]. Стаханов природа шаровой молнии. – М.: Атомиздат, 1979. С. 103 – 176.
[14]. , Розанов вероятностей. – М.: Наука, 1987. С. 43 – 57.
[15]. , Осипов . – М.: Наука, 1981. С. 11 – 22, 93, 104, 139, 150
[16]. Сердюк организма с электромагнитными полями. – К.: Наукова Думка, 1977.
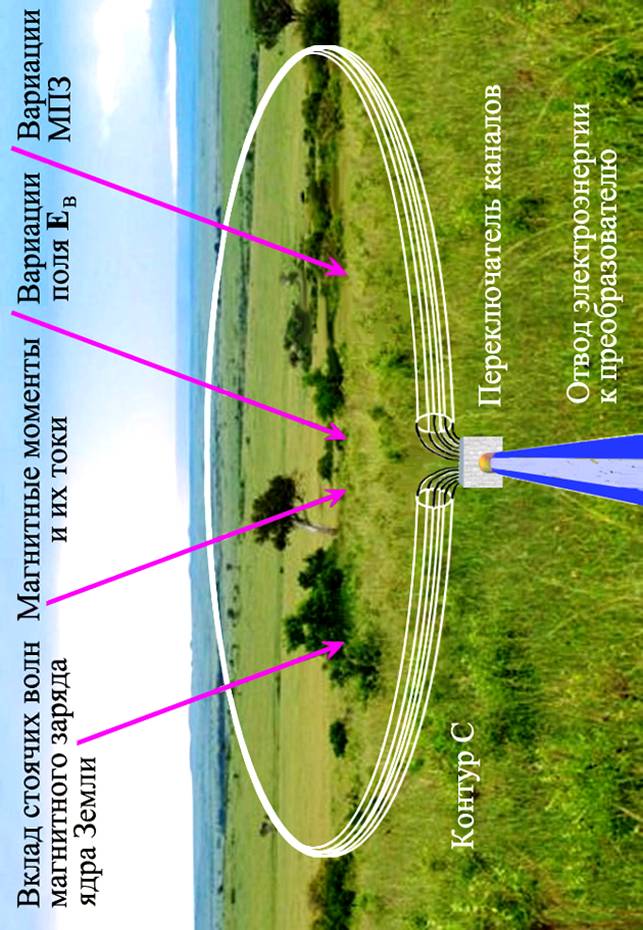 Приложение 1. Вклады в Э. Д.С. контура С на дневной поверхности.
Приложение 1. Вклады в Э. Д.С. контура С на дневной поверхности.