характеристик большого числа испытаний к некоторым определенным постоянным.
Теорема. Для любой случайной величины, имеющей математическое ожидание и дисперсию, справедливо неравенство Чебышева:
![]()
где ![]() ,
, ![]() .
.
Учитывая, что события 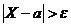 и
и ![]() противоположны, неравенство Чебышева можно записать и в другой форме:
противоположны, неравенство Чебышева можно записать и в другой форме:
![]()
Неравенство Чебышева применимо для любых случайных величин. В форме оно устанавливает верхнюю границу, а в форме — нижнюю границу вероятности
рассматриваемого события.
Теорема Чебышева. Если дисперсии ![]() независимых случайных величин
независимых случайных величин ![]() ограничены одной и той же постоянной, то при неограниченном увеличении числа
ограничены одной и той же постоянной, то при неограниченном увеличении числа ![]() средняя арифметическая случайных величин сходится по вероятности к средней
средняя арифметическая случайных величин сходится по вероятности к средней
арифметической их математических ожиданий ![]() , т. е.
, т. е.
![]() ,
,
или
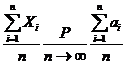
Выясним теперь смысл формулировки «сходимость по вероятности» и записи ее содержания в виде. Понятие предела переменной величины ![]() (
(![]() или
или ![]() при
при ![]() ) означает, что начиная с некоторого момента ее изменения для
) означает, что начиная с некоторого момента ее изменения для
любого (даже сколь угодно малого) числа ![]() будет верно неравенство
будет верно неравенство ![]() . В круглых скобках выражения содержится аналогичное выражение
. В круглых скобках выражения содержится аналогичное выражение
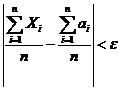
где ![]() - случайная величина, а
- случайная величина, а ![]() — постоянное число.
— постоянное число.
Однако из вовсе не следует, что это неравенство будет выполняться всегда, начиная с некоторого момента изменения ![]() . Так как
. Так как ![]() - случайная величина, то возможно, что в отдельных случаях неравенство выполняться не будет. Однако с увеличением числа
- случайная величина, то возможно, что в отдельных случаях неравенство выполняться не будет. Однако с увеличением числа ![]() вероятность неравенства
вероятность неравенства 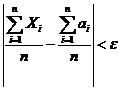 стремится к 1, т. е. это неравенство будет выполняться в подавляющем числе случаев. Другими словами, при достаточно больших
стремится к 1, т. е. это неравенство будет выполняться в подавляющем числе случаев. Другими словами, при достаточно больших ![]() выполнение рассматриваемого неравенства является событием практически достоверным, а неравенства противоположного смысла — практически невозможным.
выполнение рассматриваемого неравенства является событием практически достоверным, а неравенства противоположного смысла — практически невозможным.
Таким образом, стремление ![]() к
к ![]() следует понимать не как категорическое утверждение, а как утверждение, верность которого гарантируется с вероятностью, сколь угодно близкой к 1 при
следует понимать не как категорическое утверждение, а как утверждение, верность которого гарантируется с вероятностью, сколь угодно близкой к 1 при ![]() . Это обстоятельство и отражено
. Это обстоятельство и отражено
в формулировке теоремы «сходится по вероятности» и в записи обозначением ![]() .
.
Подчеркнем смысл теоремы Чебышева. При большом числе ![]() случайных величин
случайных величин 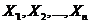 практически достоверно, что их средняя
практически достоверно, что их средняя ![]() — величина случайная, как угодно мало отличается от неслучайной величины
— величина случайная, как угодно мало отличается от неслучайной величины ![]() , т. е. практически перестает быть случайной.
, т. е. практически перестает быть случайной.
Следствие. Если независимые случайные величины ![]() имеют одинаковые математические ожидания, равные
имеют одинаковые математические ожидания, равные ![]() , а их дисперсии ограничены одной и той же постоянной, то формулы, примут вид:
, а их дисперсии ограничены одной и той же постоянной, то формулы, примут вид:
![]() ,
,
или
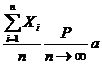 .
.
Теорема Чебышева и ее следствие имеют большое практическое значение. Например, страховой компании необходимо установить размер страхового взноса, который должен уплачивать страхователь; при этом страховая компания обязуется выплатить при наступлении страхового случая определенную страховую сумму. Рассматривая частоту/убытки страхователя при наступлении страхового случая как величину случайную и обладая известной статистикой таких случаев, можно определить среднее число/средние убытки при наступлении страховых случаев, которое на основании теоремы Чебышева с большой степенью уверенности можно считать величиной почти не случайной. Тогда на основании этих данных и предполагаемой страховой суммы определяется размер страхового взноса. Без учета действия закона больших чисел (теоремы Чебышева) возможны существенные убытки страховой компании (при занижении размера страхового взноса), либо потеря привлекательности страховых услуг (при завышении размера взноса).
Закон больших чисел устанавливает факт приближения средней большого числа случайных величин к определенным постоянным. Но этим не ограничиваются закономерности, возникающие в результате суммарного действия случайных величин. Оказывается, что при некоторых условиях совокупное действие случайных величин
приводит к определенному, а именно — к нормальному закону распределения.
Центральная предельная теорема представляет собой группу теорем, посвященных установлению условий, при которых возникает нормальный закон распределения. Среди этих теорем важнейшее место принадлежит теореме Ляпунова.
Теорема Ляпунова. Если ![]() — независимые случайные величины, у каждой из которых существует математическое ожидание
— независимые случайные величины, у каждой из которых существует математическое ожидание ![]() , дисперсия
, дисперсия ![]() , абсолютный центральный момент третьего порядка
, абсолютный центральный момент третьего порядка ![]() и
и
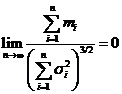 ,
,
то закон распределения суммы ![]() при
при ![]() неограниченно приближается к нормальному с математическим ожиданием
неограниченно приближается к нормальному с математическим ожиданием ![]() и дисперсией
и дисперсией ![]() .
.
Смысл условия состоит в том, чтобы в сумме ![]() не было слагаемых, влияние которых на рассеяние
не было слагаемых, влияние которых на рассеяние ![]() подавляюще велико по сравнению с влиянием всех остальных, а также не должно быть большого числа случайных слагаемых, влияние которых очень мало по сравнению с суммарным влиянием остальных. Таким образом, удельный вес каждого отдельного слагаемого должен стремиться к нулю при увеличении числа слагаемых.
подавляюще велико по сравнению с влиянием всех остальных, а также не должно быть большого числа случайных слагаемых, влияние которых очень мало по сравнению с суммарным влиянием остальных. Таким образом, удельный вес каждого отдельного слагаемого должен стремиться к нулю при увеличении числа слагаемых.
Так, например, потребление электроэнергии для бытовых нужд за месяц в каждой квартире многоквартирного дома можно представить в виде ![]() различных случайных величин. Если потребление электроэнергии в каждой квартире по своему значению резко не выделяется среди остальных, то на основании теоремы Ляпунова можно считать, что потребление электроэнергии всего дома, т. е. сумма
различных случайных величин. Если потребление электроэнергии в каждой квартире по своему значению резко не выделяется среди остальных, то на основании теоремы Ляпунова можно считать, что потребление электроэнергии всего дома, т. е. сумма ![]() независимых случайных величин будет случайной величиной, имеющей приближенно нормальный закон распределения. Если, например, в одном из помещений дома разместится вычислительный центр, у которого уровень потребления электроэнергии несравнимо выше, чем в каждой квартире
независимых случайных величин будет случайной величиной, имеющей приближенно нормальный закон распределения. Если, например, в одном из помещений дома разместится вычислительный центр, у которого уровень потребления электроэнергии несравнимо выше, чем в каждой квартире
для бытовых нужд, то вывод о приближенно нормальном распределении потребления электроэнергии всего дома будет неправомерен, так как нарушено условие, ибо потребление электроэнергии вычислительного центра будет играть превалирующую роль в образовании всей суммы потребления.
Следствие. Если ![]() — независимые случайные величины, у которых существуют равные математические ожидания
— независимые случайные величины, у которых существуют равные математические ожидания ![]() , дисперсии
, дисперсии ![]() и абсолютные центральные моменты третьего порядка
и абсолютные центральные моменты третьего порядка ![]()
![]() , то закон распределения суммы
, то закон распределения суммы ![]() при
при ![]() неограниченно приближается к нормальному закону.
неограниченно приближается к нормальному закону.
ТЕМА 14. ОСНОВЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ.
ОСНОВЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Основные понятия математической статистики. Генеральная совокупность. Выборка. Представительная выборка. Выборочное математическое ожидание и дисперсия.
В практике статистических наблюдений различают два вида наблюдений: сплошное, когда изучаются все объекты совокупности, и не сплошное, выборочное, когда изучается часть объектов. Примером сплошного наблюдения является перепись населения, охватывающая все население страны. Выборочными наблюдениями является, например, проводимые
социологические исследования, охватывающие часть населения страны, области, района и т. д.
Вся подлежащая изучению совокупность объектов (наблюдений) называется генеральной совокупностью. В математической статистике понятие генеральной совокупности трактуется как совокупность всех мыслимых наблюдений, которые могли бы быть произведены при данном реальном комплексе условий, и в этом смысле его не следует
смешивать с реальными совокупностями, подлежащими статистическому изучению.
Понятие генеральной совокупности в определенном смысле аналогично понятию случайной величины (закону распределения вероятностей, вероятностному пространству), так как полностью обусловлено определенным комплексом условий.
Та часть объектов, которая отобрана для непосредственного изучения из генеральной совокупности, называется выборочной совокупностью, или выборкой. Числа объектов (наблюдений) в генеральной или выборочной совокупности называются их объемами.
Сущность выборочного метода состоит в том, чтобы по некоторой части генеральной
совокупности (по выборке) выносить суждение о ее свойствах в целом.
Выборка называется репрезентативной (представительной), если она достаточно хорошо воспроизводит генеральную совокупность.
Различают следующие виды выборок:
• собственно-случайная выборка, образованная случайным выбором элементов без расчленения на части или группы;
• механическая выборка, в которую элементы из генеральной совокупности отбираются через определенный интервал. Например, если объем выборки должен составлять 10% (10%-ная выборка), то отбирается каждый 10-й ее элемент и т. д.;
• типическая {стратифицированная) выборка, в которую случайным образом отбираются элементы из типических групп, на которые по некоторому признаку разбивается
генеральная совокупность;
• серийная {гнездовая) выборка, в которую случайным образом отбираются не элементы, а целые группы совокупности (серии), а сами серии подвергаются сплошному
наблюдению.
Используют два способа образования выборки:
• повторный отбор (по схеме возвращенного шара), когда каждый элемент, случайно отобранный и обследованный, возвращается в общую совокупность и может быть
повторно отобран;
• бесповторный отбор (по схеме невозвращенного шара), когда отобранный элемент не возвращается в общую совокупность.
Средние арифметические распределения признака в генеральной и выборочной совокупностях называются соответственно генеральной и выборочной средними, а дисперсии этих распределений — генеральной и выборочной дисперсиями.
Важнейшей задачей выборочного метода является оценка параметров (характеристик) генеральной совокупности по данным выборки. Теоретическую основу применимости выборочного метода составляет закон больших чисел, согласно которому при неограниченном увеличении объема выборки практически достоверно, что случайные выборочные характеристики как угодно близко приближаются (сходятся по вероятности) к определенным параметрам генеральной совокупности.
Вариационный ряд. Эмпирическая функция распределения. Полигон и гистограмма.
Пусть из генеральной совокупности извлечена некоторая выборка, причем значение признака ![]() наблюдалось
наблюдалось ![]() раз, причем:
раз, причем:
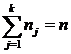
Наблюдаемые значения ![]() принято называть вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом. Числа
принято называть вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом. Числа ![]() наблюдений называют частотами, а их отношения к объему выборки
наблюдений называют частотами, а их отношения к объему выборки ![]() называют относительными частотами.
называют относительными частотами.
Статистическим распределением выборки называется перечень вариант и соответствующих им частот или относительных частот.
Статистическое распределение можно задать также в виде последовательности непересекающихся интервалов значений исследуемого признака и соответствующих им частот. При этом в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал.
Пусть известно статистическое распределение частот количественного признака Х. Обозначим через ![]() число наблюдений, при которых наблюдалось значение признака, меньшее Х, а через
число наблюдений, при которых наблюдалось значение признака, меньшее Х, а через ![]() общее число наблюдений, т. е. объем выборки. В этих обозначениях относительная частота события
общее число наблюдений, т. е. объем выборки. В этих обозначениях относительная частота события ![]() будет равна
будет равна ![]() . В общем случае относительная частота является функцией аргумента
. В общем случае относительная частота является функцией аргумента ![]() . Поскольку эта функция выводится опытным (эмпирическим) путем, то ее обычно называют эмпирической.
. Поскольку эта функция выводится опытным (эмпирическим) путем, то ее обычно называют эмпирической.
Эмпирической функцией распределения (или функцией распределения выборки) называется функция ![]() , определяющая для каждого значения х относительную частоту события
, определяющая для каждого значения х относительную частоту события ![]() :
:
![]() ,
,
где ![]() – число вариант, меньших
– число вариант, меньших ![]() ;
; ![]() – объем выборки.
– объем выборки.
В отличие от эмпирической функции распределения выборки 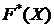 функцию распределения
функцию распределения ![]() генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями состоит в том, что теоретическая функция
генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями состоит в том, что теоретическая функция ![]() определяет вероятность события
определяет вероятность события ![]() , а эмпирическая функция
, а эмпирическая функция ![]() определяет относительную частоту этого же события. Из теоремы Бернулли следует, что относительная частота события
определяет относительную частоту этого же события. Из теоремы Бернулли следует, что относительная частота события ![]() , т. е. функция
, т. е. функция ![]() стремится по вероятности к вероятности
стремится по вероятности к вероятности ![]() этого события. Другими словами, при достаточно больших
этого события. Другими словами, при достаточно больших ![]() числа
числа ![]() и
и ![]() мало отличаются одно от другого в том смысле, что:
мало отличаются одно от другого в том смысле, что:
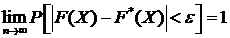 .
.
Уже отсюда следует обоснованная возможность использования эмпирической функции распределения выборки для приближенного представления теоретической выборки распределения генеральной совокупности. Более того, совсем не трудно убедиться в том, что функция ![]() обладает теми же основными свойствам, что и функция
обладает теми же основными свойствам, что и функция ![]() .
.
Таким образом, эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности. В целях обеспечения наглядности принято изображать статистические распределения в графическом виде, наиболее часто, в виде полигона и гистограммы.
Полигоном частот называется ломаная линия, отрезки которой соединяют точки ![]() , при этом по оси абсцисс откладывают варианты
, при этом по оси абсцисс откладывают варианты ![]() , а по оси ординат – соответствующие им частоты
, а по оси ординат – соответствующие им частоты ![]() .
.
Полигоном относительных частот называется ломаная, отрезки которой соединяют точки ![]() .
.
В случае, если исследуемый признак является непрерывной случайной величиной, целесообразнее использовать гистограмму. Для ее построения интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько непересекающихся частичных интервалов длиной ![]() и находят для каждого
и находят для каждого ![]() -го интервала величину
-го интервала величину ![]() – сумму частот вариант, попавших в это
– сумму частот вариант, попавших в это ![]() -й интервал.
-й интервал.
Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиною ![]() , а высоты равны отношениям
, а высоты равны отношениям ![]() , т. е. плотностям частоты.
, т. е. плотностям частоты.
Очевидно, что площадь гистограммы частот равна сумме всех частот, т. е. объему выборки ![]() .
.
Гистограммой относительных частот называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат интервалы длиною ![]() , а высоты равны отношению
, а высоты равны отношению ![]() .
.
Очевидно, что площадь гистограммы относительных частот равна сумме всех относительных частот, т. е. единице.
СТАТИСТИЧЕСКИЕ ОЦЕНКИ. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ.
Понятие статистической оценки. Несмещенные, эффективные и состоятельные оценки.
Несмещенной называют статистическую оценку ![]() , математическое ожидание которой равно оцениваемому параметру
, математическое ожидание которой равно оцениваемому параметру ![]() при любом объеме выборки, т. е.:
при любом объеме выборки, т. е.: ![]() .
.
Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.
Эффективной называют статистическую оценку, которая при заданном объеме выборки ![]() имеет наименьшую возможную дисперсию.
имеет наименьшую возможную дисперсию.
При рассмотрении выборок большого объема к статистическим оценкам предъявляется требование состоятельности.
Состоятельной называют статистическую оценку, которая при ![]() стремится по вероятности к оцениваемому параметру.
стремится по вероятности к оцениваемому параметру.
Генеральная и выборочная средние. Оценка генеральной средней по выборочной средней. Генеральная и выборочная дисперсии. Оценка генеральной дисперсии по исправленной выборочной.
Пусть изучается дискретная генеральная совокупность относительно количественного признака X.
Генеральной средней ![]() называется среднее арифметическое значений признака генеральной совокупности.
называется среднее арифметическое значений признака генеральной совокупности.
Если все значения ![]() признака генеральной совокупности объема
признака генеральной совокупности объема ![]() различны, величину
различны, величину ![]() рассчитывают по формуле:
рассчитывают по формуле:
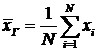 .
.
Если же значения признака ![]() имеют соответственно частоты
имеют соответственно частоты ![]() , причем выполняется условие:
, причем выполняется условие: 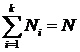 , то величину генеральной средней рассчитывают по формуле:
, то величину генеральной средней рассчитывают по формуле:
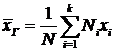 .
.
Пусть теперь для изучения некоторой генеральной совокупности относительно количественного признака X извлечена выборка объема ![]() .
.
Выборочной средней ![]() называется среднее арифметическое значение признака выборочной совокупности.
называется среднее арифметическое значение признака выборочной совокупности.
Для вычисления величины ![]() используются формулы аналогичные по структуре формулам для величины
используются формулы аналогичные по структуре формулам для величины ![]() с тем лишь отличием, что вместо
с тем лишь отличием, что вместо ![]() и
и ![]() используются величины
используются величины ![]() и
и ![]() , т. е.:
, т. е.:
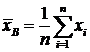 и
и 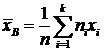 .
.
Для того чтобы охарактеризовать рассеяние значений количественного признака ![]() генеральной совокупности относительно среднего значения вводят сводную характеристику – генеральную дисперсию.
генеральной совокупности относительно среднего значения вводят сводную характеристику – генеральную дисперсию.
Генеральной дисперсией ![]() называется среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения – генеральной средней
называется среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения – генеральной средней ![]() .
.
Если все значения ![]() признака генеральной совокупности объема
признака генеральной совокупности объема ![]() различны, то величина
различны, то величина ![]() рассчитывается по формуле:
рассчитывается по формуле:
 .
.
Если же значения признака ![]() имеют соответственно частоты
имеют соответственно частоты ![]() , причем:
, причем: 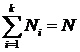 , то применяется формула:
, то применяется формула:
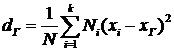 .
.
Рассеяние значений признака генеральной совокупности можно также охарактеризовать другой сводной характеристикой – средним квадратичным отклонением.
Генеральным средним квадратичным отклонением называется квадратный корень из генеральной дисперсии: ![]() .
.
Для того чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки вокруг выборочной средней ![]() , вводят сводную характеристику – выборочную дисперсию.
, вводят сводную характеристику – выборочную дисперсию.
Выборочной дисперсией ![]() называется среднее арифметическое квадратов отклонений наблюдаемых значений признака от их среднего значения
называется среднее арифметическое квадратов отклонений наблюдаемых значений признака от их среднего значения ![]() .
.
Для вычисления величины ![]() используются формулы аналогичные по структуре формулам для величины
используются формулы аналогичные по структуре формулам для величины ![]() с тем лишь отличием, что вместо
с тем лишь отличием, что вместо ![]() ,
, ![]() и
и ![]() используются величины:
используются величины: ![]() ,
, ![]() и
и ![]() .
.
Указанные формулы имеют вид:
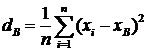 и
и 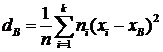 .
.
Выборочным средним квадратичным отклонением называется квадратный корень из выборочной дисперсии, т. е.: ![]() .
.
Вычисление дисперсии, безразлично – выборочной или генеральной, можно существенно упростить, используя следующую теорему.
Теорема. Дисперсия равна среднему квадратов значений признака за вычетом квадрата общей средней: ![]() .
.
Пусть теперь по данным выборки объемом n требуется оценить неизвестную генеральную дисперсию ![]() . Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то эта оценка будет приводить к систематическим ошибкам, давая заниженное значение генеральной дисперсии. Объяснить это можно тем, что выборочная дисперсия
. Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то эта оценка будет приводить к систематическим ошибкам, давая заниженное значение генеральной дисперсии. Объяснить это можно тем, что выборочная дисперсия ![]() является смещенной оценкой величины
является смещенной оценкой величины ![]() .
.
Таким образом, для того, чтобы получить несмещенную оценку генеральной дисперсии, нужно «исправить» выборочную дисперсию, умножив ее на дробь 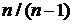 , т. е.:
, т. е.:
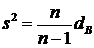
Замечание. На практике операцию исправления используют для выборок с объемом ![]() . Для больших объемов очевидно
. Для больших объемов очевидно ![]() , тем точнее, чем больше объем
, тем точнее, чем больше объем ![]() .
.
Можно показать, что выборочное среднее квадратичным отклонение ![]() также является смещенной оценкой генерального среднего квадратичным отклонения
также является смещенной оценкой генерального среднего квадратичным отклонения ![]() , т. е.:
, т. е.:
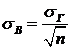 .
.
Точечная и интервальная оценки. Доверительный интервал.
Точечной называется оценка, которая определяется одним числом.
Интервальной называется оценка, которая определяется двумя числами – концами интервала.
Интервальные оценки позволяют установить точность и надежность оценок. Разъясним смысл этих новых понятий. Пусть найденная по данным выборки статистическая характеристика ![]() служит оценкой неизвестного параметра
служит оценкой неизвестного параметра ![]() . Будем считать
. Будем считать![]() постоянным числом, тогда очевидно, чем меньше модуль разности
постоянным числом, тогда очевидно, чем меньше модуль разности ![]() , тем точнее оценка
, тем точнее оценка ![]() определяет параметр
определяет параметр ![]() . Другими словами, если
. Другими словами, если ![]() и
и ![]() , то чем меньше
, то чем меньше ![]() , тем оценка точнее, т. е. число
, тем оценка точнее, т. е. число ![]() есть характеристика точности оценки. Однако статистические методы не позволяют категорически однозначно утверждать, что оценка
есть характеристика точности оценки. Однако статистические методы не позволяют категорически однозначно утверждать, что оценка ![]() удовлетворяет неравенству
удовлетворяет неравенству 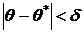 , можно лишь говорить о вероятности γ, с которой это неравенство может осуществляться.
, можно лишь говорить о вероятности γ, с которой это неравенство может осуществляться.
Надежностью (или доверительной вероятностью) оценки параметра ![]() по
по ![]() называется вероятность
называется вероятность ![]() , с которой осуществляется неравенство
, с которой осуществляется неравенство ![]() .
.
Замечание. Обычно надежность оценки задается наперед, причем в качестве ![]() выбирают число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.
выбирают число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.
Пусть вероятность того, что |![]() равна
равна ![]() , т. е.
, т. е. ![]() . Заменив неравенство
. Заменив неравенство ![]() равносильным ему двойным неравенством
равносильным ему двойным неравенством ![]() , получим:
, получим: ![]() . Последнее соотношение следует понимать так: вероятность того, что интервал
. Последнее соотношение следует понимать так: вероятность того, что интервал ![]() заключает в себе (покрывает) неизвестный параметр
заключает в себе (покрывает) неизвестный параметр ![]() , равна
, равна ![]() .
.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 |




