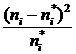Математика. Часть 2. Лекция 5. Интегральное исчисление функции одной переменной (стр. 8 )

Доверительным называется интервал , который покрывает неизвестный параметр с заданной надежностью (доверительной вероятностью) .

Замечание 1. Доверительный интервал в общем случае имеет случайные концы (так называемые доверительные границы).

Замечание 2. Поскольку случайной величиной является не оцениваемый параметр , а доверительный интервал, то более правильно говорить не о вероятности попадания в доверительный интервал, а о вероятности того, что доверительный интервал покроет параметр .

Доверительный интервал для оценки математического ожидания нормального распределения.

Пусть случайная величина имеет нормальное распределение и известно ее среднее квадратичное отклонение . Требуется найти доверительный интервал (точнее доверительные границы интервала), покрывающий математическое ожидание 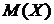с надежностью , с учетом полученного значения выборочной средней .

Как отмечалось, выборочная средняя является случайной величиной, поэтому ее можно обозначить через . Как установлено выше, математическое ожидание выборочной средней равно , т. е. . Среднее квадратичное отклонение выборочной средней равно: , где – объем выборки.

Будем считать, что вероятность попадания выборочного среднего в некоторую, пока еще неизвестную, – окрестность математического ожидания задана и равна , т. е.: .

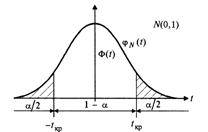
Как известно, для нормально распределенной случайной величины имеет место равенство: 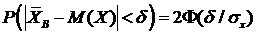, где через обозначено значение функции Лапласа в точке .

Функцией Лапласа (или интегралом вероятностей) называется интеграл

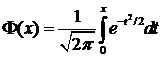
Учитывая, что выборочное среднее, как среднее арифметическое нормально распределенных случайных величин распределено нормально, подставляя в последнее равенство вместо величину , а вместо величину получим:

,

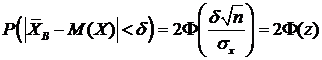где 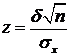, откуда получим .

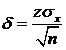Если теперь подставить найденное выражение для величины в левую часть последнего равенства и преобразовать ее, используя свойство модуля, получим:

.

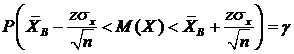Именно этот доверительный интервал и покрывает неизвестное 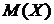с надежностью . При этом число z определяется из равенства: , т. е. по таблице значений функции Лапласа находится значение , соответствующее значению функции, равному .

Доверительный интервал для оценки математического ожидания нормального распределения при неизвестном σ.

Пусть признак X генеральной совокупности распределен нормально, причем среднее квадратичное отклонение σ неизвестно. Требуется оценить неизвестное математическое ожидание с помощью доверительного интервала.

В рассматриваемом случае по данным выборки можно построить случайную величину (ее возможные значения обозначим через t):

,

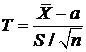которая имеет распределение Стьюдента с степенями свободы; здесь – выборочная средняя, – исправленное среднее квадратичное отклонение, – объем выборки.

Как мы уже видели, распределение Стьюдента определяется только одним параметром – числом степеней свободы – и не зависит от неизвестных параметров и σ. Поскольку плотность распределения Стьюдента s(t, n) есть четная функция от t, вероятность осуществления неравенства:

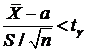
определяется так:

.

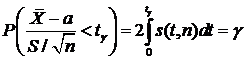Заменив неравенство в круглых скобках равносильным ему двойным неравенством, получим:

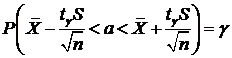
Следовательно, пользуясь распределением Стьюдента, мы нашли доверительный интервал, покрывающий неизвестный параметр с надежностью (доверительной вероятностью) γ. Если заменить случайные величины и неслучайными величинами и , найденными по выборке, то искомый интервал будет иметь вид: , где величину можно найти по заданным и , используя таблицы.

Статистическая гипотеза. Ошибки первого и второго рода.

Статистической называется гипотеза о виде неизвестного распределения, или о параметрах известных распределений.

Наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза. По этой причине эти гипотезы целесообразно различать.

Нулевой или основной называется выдвинутая гипотеза . Конкурирующей или альтернативной называют гипотезу , которая противоречит основной.

Различают гипотезы, которые содержат только одно и более одного предположений.

Простой называется гипотеза, содержащая только одно предположение.

Гипотеза : математическое ожидание нормального распределения равно 4 (σ известно) – простая.

Сложной называется гипотеза, которая состоит из конечного или бесконечного числа простых гипотез.

Гипотеза : математическое ожидание нормального распределения равно 7 (σ

неизвестно) – сложная.

Выбранная гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки. Поскольку проверку производят статистическими методами, ее называют статистической. В результате проверки может быть принято правильное или неправильное решение. Поэтому различают ошибки двух родов.

Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.

Например, пусть основная гипотеза состоит в том, что предприятие получает прибыль при определенном вложении ресурсов. Если это правильная гипотеза, то ошибка первого рода состоит в том, что данная гипотеза отвергается. Если же принимается гипотеза, что прибыль предприятие не получит, то это ошибка второго рода.

Обычно ошибка первого рода влечет за собой ошибку второго рода. Так, если отвергнута гипотеза о том, что предприятие получает прибыль, то, естественно, принимается решение о том, что оно прибыли не имеет.

Однако на практике возможны и другие ситуации. В большинстве случае рассматриваются гипотезы о законах распределения. Если отвергается правильный закон распределения, то совершается ошибка первого рода. Но после этого может быть принято решение уточнить данные, т. е. другая гипотеза не принимается. Если же принимается другое распределение, то совершается ошибка второго рода.

Вероятность совершить ошибку первого рода принято обозначать α и называть уровнем значимости. Наиболее часто уровень значимости принимают равным 0,05 или 0,01. Если принимается уровень значимости α = 0,05, то это значит, что в пяти случаях из ста имеется риск допустить ошибку первого рода, т. е. отвергнуть правильную гипотезу.

Статистический критерий проверки нулевой гипотезы.

Статистическим критерием (или просто критерием) называется случайная величина , которая служит для проверки нулевой гипотезы.

Например, если проверяют гипотезу о равенстве дисперсий двух нормальных генеральных совокупностей, то в качестве критерия принимают отношение исправленных выборочных дисперсий:

.

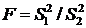Эта величина случайная, так как в различных опытах дисперсии принимают различные, наперед неизвестные значения, и распределена по критерию Фишера – Снедекора.

Для проверки гипотезы по данным выборок вычисляют частные значения входящих в критерий величин и таким образом получают частное (наблюдаемое) значение критерия.

Наблюдаемым значением называют значение критерия, найденное (вычисленное) по выборкам.

Например, если по двум выборкам найдены исправленные выборочные дисперсии и , то наблюдаемое значение критерия составит: .

Область принятия гипотезы.

После выбора определенного критерия множество всех его возможных значений разбивают на два непересекающихся подмножества: одно из них содержит значение критерия, при котором нулевая гипотеза отвергается, а другая, при котором она принимается.

Критической областью называется совокупность значений критерия, при которой нулевую гипотезу отвергают.

Областью принятия гипотезы (областью допустимых значений) называется совокупность значений критерия, при которых гипотезу принимают.

Основной принцип проверки статистических гипотез можно сформулировать следующим образом: если наблюдаемое значение критерия принадлежит критической области, то гипотезу отвергают, если же наблюдаемое значение критерия принадлежит области принятия гипотезы, то гипотезу принимают.

Поскольку критерий есть одномерная случайная величина, то ее возможные значения принадлежат некоторому интервалу. Поэтому критическая область и область принятия гипотезы также являются интервалами и, следовательно, существуют точки, которые их разделяют.

Критическими точками (границами) называются точки, которые отделяют критическую область от области принятия гипотезы.

Критические области разделяются на правосторонние и левосторонние.

Правосторонней называют критическую область, определяемую неравенством , где – положительное число.

Левосторонней называют критическую область, определяемую неравенством , где – отрицательное число.

Существуют и двусторонние области, определяемые неравенствами 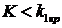; , где .

Для отыскания правосторонней критической области достаточно найти критическую точку . Для ее нахождения задаются достаточно малой вероятностью – уровнем значимости α. Затем ищут критическую точку , исходя из требования, чтобы при условии справедливости нулевой гипотезы вероятность того, что критерий примет значение, большее , была равна принятому уровню значимости . Для каждого критерия имеются соответствующие таблицы, по которым и находят критическую точку, удовлетворяющую этому требованию.

Когда критическая точка найдена, вычисляют по данным выборки (или выборок) наблюденное значение критерия и, если окажется, что , то нулевую гипотезу отвергают, в противном случае – принимают.

Наблюдаемое значение критерия может оказаться большим не потому, что нулевая гипотеза ложна, а по каким-то другим причинам (малый объем выборки, недостатки методики эксперимента и др.). В этом случае, отвергнув правильную нулевую гипотезу, совершают ошибку первого рода. Вероятность этой ошибки равна уровню значимости α, поэтому, пользуясь этим требованием, мы рискуем совершить ошибку первого рода.

Отыскание левосторонней и двусторонней критических областей также сводится к нахождению соответствующих критических точек.

Ясно, что критические точки, удовлетворяющие этому требованию, могут быть выбраны бесчисленным количеством способов. На практике наиболее часто используют соотношение:

.

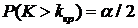Для нахождения критической области можно использовать не только принципы и соотношения, приведенные выше, но и понятие мощности критерия.

Мощностью критерия называют вероятность попадания критерия в критическую область при условии, что справедлива конкурирующая гипотеза, или, другими словами, вероятность того, что нулевая гипотеза будет отвергнута, если верна конкурирующая гипотеза.

Пусть для проверки гипотезы принят определенный уровень значимости и выборка имеет фиксированный объем. Вероятность ошибки второго рода равна β, следовательно мощность равна (1 – β). Очевидно, что мощность критерия должна быть максимальной, что может быть достигнуто при уменьшении ошибки второго рода β. Следовательно, если уровень значимости выбран, то критическую область следует строить так, чтобы мощность критерия была максимальной.

Сравнение двух средних нормальных генеральных совокупностей.

Пусть имеются две совокупности и , характеризуемые генеральными средними и и известными дисперсиями и . Необходимо проверить гипотезу равенстве генеральных средних, т. е. : . Для проверки гипотезы из этих совокупностей взяты две независимые выборки объемов и , по которым найдены средние арифметические и и выборочные дисперсии и .

При достаточно больших объемах выборки выборочные средние и имеют приближенно нормальный закон распределения, соответственно и .

В случае справедливости гипотезы разность имеет нормальный закон распределения с математическим ожиданием

и дисперсией 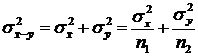(напомним, что дисперсия разности независимых случайных величин равна сумме их дисперсий, а дисперсия средней независимых слагаемых в раз меньше дисперсии каждого).

Поэтому при выполнении гипотезы статистика

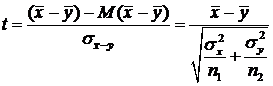
стандартное нормальное распределение .

В случае конкурирующей гипотезы (или ) выбирают одностороннюю критическую область и критическое значение статистики находят из

условия

,

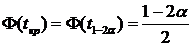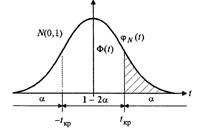
а при конкурирующей гипотезе выбирают двустороннюю критическую область и критическое значение статистики находят из условия

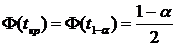
Если фактически наблюдаемое значение статистики больше критического , определенного на уровне значимости (по абсолютной величине), т. е., то гипотеза отвергается. Если , то делается вывод, что нулевая гипотеза не противоречит имеющимся наблюдениям.

Сравнение двух дисперсий нормальных генеральных совокупностей.

Пусть имеются две нормально распределенные генеральные совокупности и . Из этих совокупностей извлекают выборки объемами и , после чего находят исправленные выборочные значения дисперсий и .

Требуется по исправленным дисперсиям при заданном уровне значимости α проверить нулевую гипотезу, состоящую в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой: : .

Поскольку исправленные дисперсии являются несмещенными оценками генеральных дисперсий, наша нулевая гипотеза примет вид: : .

Таким образом, поставленная задача сводится к проверке равенства математических ожиданий исправленных выборочных дисперсий, или значимо (существенно) или незначимо различаются исправленные дисперсии.

Если окажется, что нулевая гипотеза справедлива, то различие исправленных дисперсий незначимо и объясняется случайным отбором объектов выборки.

В качестве критерия проверки нулевой гипотезы о равенстве генеральных дисперсий примем отношение большей исправленной дисперсии к меньшей, т. е. случайную величину:

.

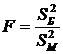Величина F при условии справедливости нулевой гипотезы имеет распределение Фишера – Снедекора со степенями свободы и , где – объем выборки для большей исправленной дисперсии, а – для меньшей.

Предположим, что большая дисперсия относится к измерениям , а меньшая – к измерениям . Тогда в качестве конкурирующей гипотезы можно принять : . В этом случае критическую область находят из условия 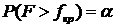, т. е. она является правосторонней. Критическую точку находят по значениям , и α по таблице распределения Фишера – Снедекора.

Далее находят по данным выборок и сравнивают с найденным предварительно . Если , то нет оснований отвергнуть нулевую гипотезу о равенстве дисперсий двух нормальных генеральных совокупностей, в противном случае нулевую гипотезу отвергают.

В тех случаях, когда конкурирующую гипотезу принимают в виде : , нужно строить двустороннюю критическую область и уровень значимости можно несколько увеличить. При этом ограничиваются нахождением правосторонней области для уровня значимости α / 2.

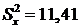Например, по двум независимым выборкам объемов и , извлеченным из нормальных генеральных совокупностей, найдены исправленные выборочные дисперсии и . При уровне значимости 0,05 проверить нулевую гипотезу : о равенстве генеральных дисперсий при конкурирующей гипотезе : .

Найдем отношение большей исправленной дисперсии к меньшей:

.

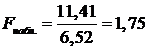Критическая область будет правосторонней. По таблице по уровню значимости 0,05 и числом степеней свободы и находим критическую точку . Так как , то нет оснований отвергнуть нулевую гипотезу.

Проверка гипотезы о распределении генеральной совокупности.

В предыдущем разделе закон распределения генеральной совокупности предполагается известным. Если закон распределения неизвестен, но есть основания предположить, что он имеет определенный вид (назовем его А), то проверяют нулевую гипотезу: генеральная совокупность распределена по закону А.

Проверка гипотезы производится при помощи специально подобранной случайной величины – критерия согласия.

Критерием согласия называется критерий проверки гипотезы о предполагаемом законе неизвестного распределения.

Существует достаточно много критериев согласия: Пирсона, Колмогорова, Смирнова. Рассмотрим наиболее употребляемый критерий согласия Пирсона или, как его еще называют, критерий χ2 – «хи-квадрат».

Пусть имеется выборка объемом , извлеченная для проверки определенного закона распределения признака генеральной совокупности, причем параметры неизвестны. Если рассматривается непрерывное распределение, то интервал возможных значений величины разбивается на непересекающихся интервалов, в каждом из которых фиксируется число попаданий вариант выборки .

Зная границы каждого интервала и принятый (предполагаемый) закон распределения генеральной совокупности, можно найти вероятность попадания случайной величины в -й интервал. После этого из формулы находится теоретическая частота появления события в -м интервале 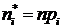. В качестве критерия выбирается случайная величина:

.

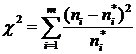При эта величина стремится к закону распределения χ2 с степенями свободы. Число степеней свободы определяется по формул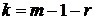е , где – число интервалов, а – число параметров, определяющих предполагаемое распределение. Так для показательного распределения , а для нормального . Далее, задавая уровень значимости α и учитывая к из таблиц распределения χ2 находят критическое значение χ2кр, для которого выполняется условие Р(χ2 > χ2кр) = α. Сравнивая вычисленное наблюдаемое значение χ2набл со значением χ2кр, принимают решение о значимости допущенной гипотезы распределения случайной величины. Если χ2набл < χ2кр – нулевую гипотезу принимают, в противном случае – отвергают.

Следует иметь в виду, что критерий согласия Пирсона, впрочем, как и любой другой, не доказывает справедливость гипотезы о предполагаемом законе распределения, а лишь устанавливает на принятом уровне значимости ее согласие или несогласие с данными наблюдений (выборки). При использовании критерия Пирсона объем выборки должен быть достаточно велик, во всяком случае, не менее 50. Каждая группа (интервал) должна содержать не менее 5 вариант, а малочисленные группы следует объединять в одну, суммируя частоты.

Пример. При уровне значимости 0,05 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты:

Эмпирические частоты 6 30 14

Теоретические частоты 337 13

Составим следующую таблицу:

Осуществим контроль расчетов χ2набл согласно формуле:

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9