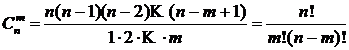
Так как по определению , то .

Свойства числа сочетаний: , .

Действия над событиями

Введем понятие суммы, произведения и разности событий.

Суммой нескольких событий называется событие, состоящее в наступлении хотя бы одного из данных событий.

Если и — совместные события, то их сумма обозначает наступление или события , или события , или обоих событий вместе. Если и — несовместные события, то их сумма означает наступление или события , или события .

Произведением нескольких событий называется событие, состоящее в совместном наступлении всех этих событий.

Если — совместные события, то их произведение означает наступление и события , и события , и события .

Разностью двух событий и называется событие, которое состоится, если событие произойдет, а событие не произойдет.

Пример. Победитель соревнования награждается: призом (событие ), денежной премией (событие ), медалью (событие ). Что представляют собой события: а) б) ; в) ?

Решение. а) Событие состоит в награждении победителя или призом, или премией, или и тем и другим.

б) Событие состоит в награждении победителя одновременно и призом, и премией, и медалью.

в) Событие состоит в награждении победителя одновременно и призом, и премией без выдачи медали.

Теорема сложения вероятностей

Теорема. Вероятность суммы конечного числа несовместных событий равна сумме вероятностей этих событий:

Следствие 1. Сумма вероятностей событий, образующих полную группу, равна единице:

Следствие 2. Сумма вероятностей противоположных событий равна единице:

Замечание. Следует еще раз подчеркнуть, что рассмотренная теорема сложения применима только для несовместных событий и попытка ее использования для совместных событий приводит к неверным и даже абсурдным результатам. Например, пусть вероятность события — выигрыша по любому билету денежно-вещевой лотереи, , и приобретено 100 билетов (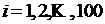). Тогда, применяя

теорему сложения, получим, что вероятность выигрыша хотя бы по одному из 100 билетов, т. е. .

Абсурдность полученного ответа (вероятность любого события не может быть больше 1) объясняется неприменимостью в данном случае теоремы сложения, ибо события 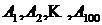являются событиями совместными.

Условная вероятность события. Теорема умножения вероятностей. Независимые события

Как отмечено выше, вероятность как мера степени объективной возможности наступления события имеет смысл при выполнении определенного комплекса условий. При изменении условий вероятность события может измениться. Так, если к

комплексу условий, при котором изучалась вероятность , добавить новое условие , то полученная вероятность события , найденная при условии, что событие произошло, называется условной вероятностью события и обозначается , или , или .

Строго говоря, «безусловная» вероятность также является условной, так как она получена при выполнении определенного комплекса условий.

Найдем формулу для вычисления условной вероятности .

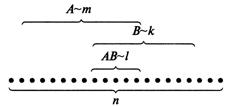
Пусть из общего числа равновозможных и несовместных (элементарных) исходов испытания (случаев) событию благоприятствует случаев, событию — случаев, а совместному появлению событий и , т. е. событию — случаев (, ).

Тогда, согласно классическому определению вероятности, , .

После того как событие произошло, число всех равновозможных исходов (случаев) сократилось с до , а число случаев, благоприятствующих событию с до . Поэтому условная вероятность

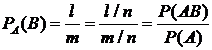
Формулу условной вероятности мы получили, опираясь на классическое определение вероятности. В общем случае эта формула служит определением условной вероятности.

Аналогично

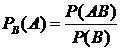
Умножая правую и левую части равенств и соответственно на и , получим

Это так называемая теорема (правило) умножения вероятностей: вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие произошло.

Теорема (правило) умножения вероятностей легко обобщается на случай произвольного числа событий: , т. е. вероятность произведения нескольких событий равна произведению вероятности одного из этих событий на условные вероятности других; при этом условная вероятность каждого последующего события вычисляется в предположении, что все предыдущие события произошли.

Теорема умножения вероятностей принимает наиболее простой вид, когда события, образующие произведение, независимы. Событие называется независимым от события , если его вероятность не меняется от того, произошло событие или нет, т. е.

.

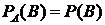В противном случае, если , событие называется зависимым от .

Если событие не зависит от , то и событие не зависит от .

Таким образом, зависимость и независимость событий всегда взаимны. Поэтому можно дать следующее определение независимости событий.

Два события называются независимыми, если появление одного из них не меняет вероятности наступления другого.

Попарная независимость нескольких событий (т. е. независимость взятых из них любых двух событий) еще не означает их независимости в совокупности.

При решении ряда задач требуется найти вероятность суммы двух или нескольких совместных событий, т. е. вероятность появления хотя бы одного из этих событий. В этом случае применять теорему сложения вероятностей в виде нельзя.

Теорема. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их произведения, т. е.

Представим событие , состоящее в наступлении хотя бы одного из двух событий и , в виде суммы трех несовместных вариантов: . Тогда по теореме сложения

Учитывая, что , , откуда , получим

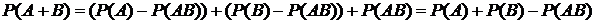
В случае трех и более совместных событий соответствующая формула для вероятности суммы весьма громоздка и проще перейти к противоположному событию : . Тогда, или

т. е. вероятность суммы нескольких совместных событий равна разности между единицей и вероятностью произведения противоположных событий . Если при этом события — независимые, то

В частном случае, если вероятности независимых событий равны, т. е. , то вероятность их суммы

Понятие случайной величины (СВ). Дискретные и непрерывные СВ. Плотность функции распределения для дискретной и непрерывной СВ. Функция распределения для дискретной и непрерывной СВ. Математическое ожидание и дисперсия СВ и их свойства.

Понятие случайной величины. Дискретные и непрерывные СВ.

Одним из важнейших понятий теории вероятностей является понятие случайной величины.

Под случайной величиной понимается переменная, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений (какое именно — заранее не известно).

Примеры случайных величин:

1) число родившихся детей в течение суток в г. Москве;

2) количество бракованных изделий в данной партии;

3) число произведенных выстрелов до первого попадания;

4) дальность полета артиллерийского снаряда;

5) расход электроэнергии на предприятии за месяц.

Случайная величина называется дискретной , если множество ее значений конечное, или бесконечное, но счетное.

Под непрерывной случайной величиной будем понимать величину, бесконечное несчетное множество значений которой есть некоторый интервал (конечный или бесконечный) числовой оси.

Так, в приведенных выше примерах 1—3 имеем дискретные случайные величины (в примерах 1 и 2 — с конечным множеством значений; в примере 3 — с бесконечным, но счетным множеством значений); а в примерах 4 и 5 — непрерывные случайные величины.

Теоретико-множественная трактовка основных понятий теории вероятностей позволяет дать следующее определение случайной величины.

Случайной величиной называется функция, заданная на множестве элементарных исходов (или в пространстве элементарных событий), т. е.

,

где — элементарный исход (или элементарное событие, принадлежащее пространству , т. е. ).

Для дискретной случайной величины множество возможных значений случайной величины, т. е. функции , конечно или счетно, для непрерывной — бесконечно и несчетно.

Случайные величины будем обозначать прописными буквами латинского алфавита ,..., а их значения — соответствующими строчными буквами ,... .

Наиболее полным, исчерпывающим описанием случайной величины является ее закон распределения.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Про случайную величину говорят, что она «распределена» по данному закону распределения или «подчинена» этому закону распределения.

Для дискретной случайной величины закон распределения может быть задан в виде таблицы, аналитически (в виде формулы) и графически.

Простейшей формой задания закона распределения дискретной случайной величины является таблица (матрица), в которой перечислены в порадке возрастания все возможные значения

случайной величины и соответствующие их вероятности, т. е.

Такая таблица называется рядом распределения дискретной случайной величины.

События , состоящие в том, что в результате испытания случайная величина примет соответственно значения являются несовместными и единственно

возможными (ибо в таблице перечислены все возможные значения случайной величины), т. е. образуют полную группу. Следовательно, сумма их вероятностей равна 1. Таким образом, для

любой дискретной случайной величины

.

(Эта единица как-то распределена между значениями случайной величины, отсюда и термин «распределение».)

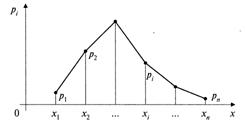
Ряд распределения может быть изображен графически, если по оси абсцисс откладывать значения случайной величины, а по оси ординат — соответствующие их вероятности. Соединение полученных точек образует ломаную, называемую многоугольником или полигоном распределения вероятностей.

Функция распределения для дискретной и непрерывной СВ

Для описания закона распределения случайной величины возможен и другой подход: рассматривать не вероятности событий для разных (как это имеет место в ряде

распределения), а вероятности события, где — текущая переменная. Вероятность , очевидно, зависит от , т. е. является некоторой функцией от .

Функцией распределения случайной величины называется функция , выражающая для каждого вероятность того, что случайная величина примет значение, меньшее .

.

Функцию иногда называют интегральной функцией распределения или интегральным законом распределения.

Геометрически функция распределения интерпретируется как вероятность того, что случайная точка попадет левее заданной точки .

Например, на рисунке показана функция распределения некоторой дискретной случайной величины.

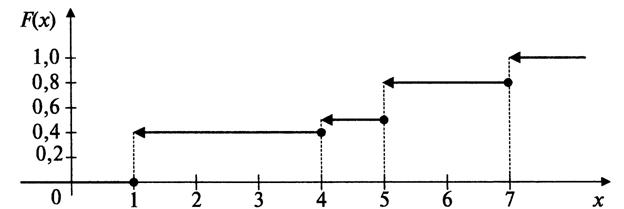
Этот пример позволяет прийти к утверждению, что функция распределения любой дискретной случайной величины есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины и

равны вероятностям этих значений. Сумма всех скачков функции равна 1.

Рассмотрим общие свойства функции распределения.

1. Функция распределения случайной величины есть неотрицательная функция, заключенная между нулем и единицей: .

2. Функция распределения случайной величины есть неубывающая функция на всей числовой оси.

3. На минус бесконечности функция распределения равна нулю, на плюс бесконечности равна единице, т. е. , .

4. Вероятность попадания случайной величины в интервал (включая ) равна приращению ее функции распределения на этом интервале, т. е.

.

Выше дано понятие непрерывной случайной величины, имеющей бесконечное несчетное

множество значений. Приведем теперь более строгое определение.

Случайная величина называется непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек.

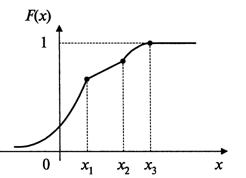
На рисунке показана функция распределения непрерывной случайной величины ,

дифференцируемая во всех точках, кроме трех точек излома.

Теорема. Вероятность любого отдельно взятого значения непрерывной случайной величины равна нулю1.

Следствие. Если — непрерывная случайная величина, то вероятность попадания случайной величины в интервал не зависит от того, является этот интервал открытым или закрытым, т. е.

.

Задание непрерывной случайной величины с помощью функции распределения не является единственным. Введем понятие плотности вероятности непрерывной

случайной величины.

Плотностью вероятности (плотностью распределения или просто плотностью) непрерывной случайной величины называется производная ее функции распределения

.

Про случайную величину говорят, что она имеет распределение (распределена) с плотностью на определенном участке оси абсцисс.

Плотность вероятности , как и функция распределения , является одной из форм закона распределения, но в отличие от функции распределения она существует только для

непрерывных случайных величин.

Плотность вероятности иногда называют дифференциальной функцией или дифференциальным законом распределения.

График плотности вероятности называется кривой распределения.

Отметим свойства плотности вероятности непрерывной случайной величины.

1. Плотность вероятности—неотрицательная функция, т. е. .

2. Вероятность попадания непрерывной случайной величины в интервал равна определенному интегралу от ее плотности вероятности в пределах от до , т. е.

.

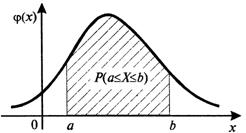
Геометрически полученная вероятность равна площади фигуры, ограниченной сверху кривой распределения и опирающейся на отрезок .

3. Функция распределения непрерывной случайной величины может быть выражена через плотность вероятности по формуле:

.

Геометрически функция распределения равна площади фигуры, ограниченной сверху кривой распределения и лежащей левее точки .

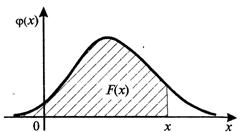
4. Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен единице:

.

Геометрически свойства 1 и 4 плотности вероятности означают, что ее график — кривая распределения — лежит не ниже оси абсцисс, и полная площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.

Математическое ожидание и дисперсия СВ и их свойства

Средним значением случайной величины является ее математическое ожидание.

Математическим ожиданием, или средним значением, дискретной случайной величины называется сумма произведений всех ее значений на соответствующие

им вероятности:

Если дискретная случайная величина принимает бесконечное, но счетное множество значений , то математическим ожиданием, или средним значением, такой дискретной случайной величины называется сумма ряда (если он абсолютно сходится):

Рассмотрим свойства математического ожидания.

1.Математическое ожидание постоянной величины равно самой постоянной:

.

2.Постоянный множитель можно выносить за знак математического ожидания, т. е.

.

3. Математическое ожидание алгебраической суммы конечного числа случайных величин равно такой же сумме их математических ожиданий, т. е.1

.

4. Математическое ожидание произведения конечного числа независимых случайных величин равно произведению их математических ожидании:

.

5.Если все значения случайной величины увеличить (уменьшить) на постоянную , то на эту же постоянную увеличится (уменьшится) математическое ожидание этой случайной величины:

.

6. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю:

.

Только математическое ожидание не может в достаточной степени характеризовать случайную величину. В качестве дополнительной характеристики рассматривается

дисперсия случайной величины. Слово дисперсия означает «рассеяние».

Дисперсией случайной величины называется математическое ожидание квадрата ее отклонения от математического ожидания:

В качестве характеристики рассеяния нельзя брать математическое ожидание отклонения случайной величины от ее математического ожидания, ибо согласно свойству 6 математического ожидания эта величина равна нулю для любой случайной величины.

Выбор дисперсии, определяемой по формуле, в качестве характеристики рассеяния значений случайной величины оправдывается также тем, что, как можно показать,

математическое ожидание квадрата отклонения случайной величины от постоянной величины минимально именно тогда, когда эта постоянная равна математическому ожиданию , т. е.

.

Если случайная величина — дискретная с конечным числом значений, то

.

Дисперсия имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину .

Средним квадратическим отклонением (стандартным отклонением или стандартом) случайной величины называется арифметическое значение корня квадратного из ее дисперсии:

.

Отметим свойства дисперсии случайной величины.

1. Дисперсия постоянной величины равна нулю:

.

2. Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат:

.

3. Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания:

.

4. Дисперсия алгебраической суммы конечного числа независимых случайных величин равна сумме их дисперсий:

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9