Математика. Часть 2. Лекция 5. Интегральное исчисление функции одной переменной (стр. 3 )

Исследование функции двух переменных на экстремум рекомендуется проводить по следующей схеме:

1°. Найти частные производные функции и .

2°. Решить систему уравнений , и найти критические точки функции.

3°. Найти частные производные второго порядка, вычислить их значения в каждой критической точке и с помощью достаточного условия сделать вывод о наличии экстремумов.

4°. Найти экстремумы (экстремальные значения) функции.

Наибольшее или наименьшее значение функции многих переменных.

При нахождении наибольшего и наименьшего значений (т. е. глобального максимума и минимума) функции нескольких переменных, непрерывной на некотором замкнутом множестве, следует иметь в виду, что эти значения достигаются или в точках экстремума, или на границе множества.

Задача нахождения максимумов и минимумов функций многих переменных значительно сложнее аналогичной задачи для функций одной переменной. Даже в самых простых случаях чисто технические проблемы могут вызвать значительные трудности.

Задаче нахождения подобных экстремумов посвящен специальный раздел математики — вариационное исчисление. В последние десятилетия бурное развитие переживает комплексная научная дисциплина — исследование операций, посвященная поиску оптимальных решений в различных, в том числе и экономических, задачах, в которых исследуемая (целевая) функция нескольких переменных принимает наибольшее или наименьшее значение.

Условный экстремум. Метод множителей Лагранжа.

Рассмотрим задачу, специфическую для функций нескольких переменных, когда ее экстремум ищется не на всей области определения, а на множестве, удовлетворяющем некоторому условию.

Пусть рассматривается функция , аргументы и которой удовлетворяют условию , называемому уравнением связи.

Точка называется точкой условного максимума (минимума), если существует такая окрестность этой точки, что для всех точек из этой окрестности, удовлетворяющих условию , выполняется неравенство ().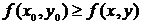

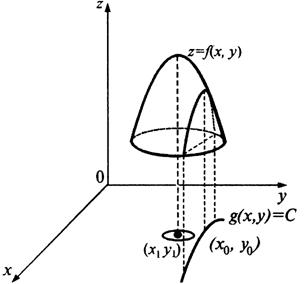
На рис. изображена точка условного максимума . Очевидно, что она не является точкой безусловного экстремума функции (на рис. это точка .

Наиболее простым способом нахождения условного экстремума функции двух переменных является сведение задачи к отысканию экстремума функции одной переменной. Допустим уравнение связи удалось разрешить относительно одной из переменных, например выразить через : . Подставив полученное выражение в функцию двух переменных, получим , т. е. функцию одной переменной. Ее экстремум и будет условным экстремумом функции .

Пример. Найти точки максимума и минимума функции при условии .

Решение. Выразим из уравнения переменную через переменную и подставим полученное выражение в функцию . Получим 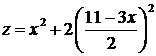или . Эта функция имеет единственный минимум при . Соответствующее значение функции . Таким образом, — точка условного экстремума (минимума).

В рассмотренном примере уравнение связи оказалось линейным, поэтому его легко удалось разрешить относительно одной из переменных. Однако в более сложных случаях сделать это не удается. Для отыскания условного экстремума в общем случае используется метод множителей Лагранжа.

Рассмотрим функцию трех переменных .

Эта функция называется функцией Лагранжа, а - множителем Лагранжа. Верна следующая теорема.

Теорема. Если точка является точкой условного экстремума функции при условии , то существует значение такое, что точка является точкой экстремума функции .

Таким образом, для нахождения условного экстремума функции при условии требуется найти решение системы

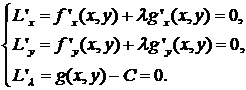
Последнее из этих уравнений совпадает с уравнением связи. Первые два уравнения системы можно переписать в виде , т. е. в точке условного экстремума градиенты функций и коллинеарны.

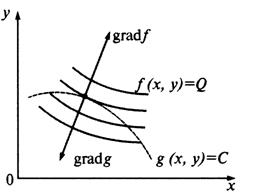
Из рис. следует, что в точке условного экстремума линия уровня функции касается линии .

Пример. Найти точки экстремума функции при условии , используя метод множителей Лагранжа.

Решение. Составляем функцию Лагранжа . Приравнивая к нулю ее частные производные, получим систему уравнений

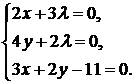
Ее единственное решение . Таким образом, точкой условного экстремума может быть только точка (3; 1). Нетрудно убедиться в том, что в этой точке функция имеет условный минимум.

В случае, если число переменных более двух, может рассматриваться и несколько уравнений связи. Соответственно в этом случае будет и несколько множителей Лагранжа. Мы не рассматриваем здесь достаточные условия условного экстремума. Отметим только, что во многих задачах критическая точка функции Лагранжа оказывается единственной и соответствует не только локальному, но и глобальному условному минимуму или максимуму.

Метод наименьших квадратов.

Пусть зависимость между двумя переменными и выражается в виде таблицы, полученной опытным путем. Это могут быть результаты опыта или наблюдений, статистической обработки материала и т. п. Требуется наилучшим образом сгладить экспериментальную зависимость между переменными и , т. е. по возможности точно отразить общую тенденцию зависимости от , исключив при этом случайные отклонения, связанные с неизбежными погрешностями измерений или статистических наблюдений. Такую сглаженную зависимость стремятся представить в виде формулы .

Формулы, служащие для аналитического представления опытных данных, получили название эмпирических формул.

Задача нахождения эмпирических формул разбивается на два этапа. На первом этапе нужно установить вид зависимости , т. е. решить, является ли она линейной, квадратичной, логарифмической или какой-либо другой. Предположим, например, что результаты экспериментальных исследований нанесены на плоскость (паре чисел соответствует точка с такими же координатами). Разумеется, существует множество кривых, проходящих через эти точки. Для продвижения к цели обычно предполагают, что кривая истинной зависимости — это наиболее «гладкая» кривая, согласованная с эмпирическими данными. Для проверки правильности вывода проводятся дополнительные исследования, т. е. производится еще ряд одновременных измерений величин и . Дополнительные точки наносятся на плоскость. Если они оказываются достаточно близкими к выбранной кривой, то можно считать, что вид кривой установлен. В противном случае кривую надо скорректировать и вновь провести дополнительные измерения.

Предположим, первый этап завершен — вид функции установлен. Тогда переходят ко второму этапу — определению неизвестных параметров этой функции. Согласно наиболее распространенному и теоретически обоснованному методу наименьших квадратов в качестве неизвестных параметров функции/(х) выбирают такие значения, чтобы сумма квадратов невязок , или отклонений «теоретических» значений , найденных по эмпирической формуле , от соответствующих опытных значений , т. е.

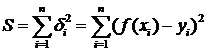
была минимальной.

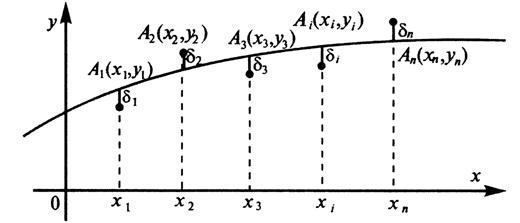
Следует отметить, что в качестве величины отклонения эмпирических точек от точек сглаживающей экспериментальную зависимость кривой в принципе можно было взять обычную сумму невязок 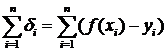или сумму их абсолютных величин 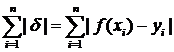, делать это нецелесообразно, так как в первом случае может быть малой или даже равняться нулю при значительном разбросе эмпирических точек, так как положительные отклонения компенсируются отрицательными. Во втором случае функция 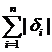лишена этого недостатка, но имеет другой — она не является дифференцируемой, что существенно затрудняет решение задачи.

Пусть в качестве функции взята линейная функция и задача сводится к отысканию таких значений параметров и , при которых функция

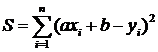
принимает наименьшее значение. Заметим, что функция есть функция двух переменных и до тех пор, пока мы не нашли, а затем зафиксировали их «наилучшие» (в смысле метода наименьших квадратов) значения, а — постоянные числа, найденные экспериментально.

Таким образом, для нахождения прямой, наилучшим образом согласованной с опытными данными, достаточно решить систему

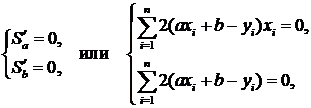
После алгебраических преобразований эта система принимает вид:

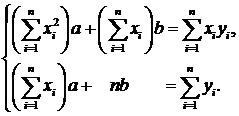
Эта система называется системой нормальных уравнений. Она имеет единственное решение, так как ее определитель

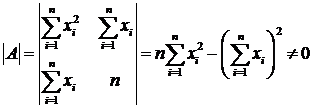
(a точнее , что можно доказать методом математической индукции при ).

Найденные значения дают минимум функции . Найдем частные производные

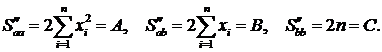
Выражение 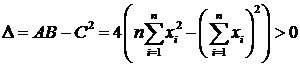в силу изложенного выше и 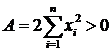, следовательно, согласно достаточному условию функция имеет единственную точку минимума, определяемую из системы нормальных уравнений. Заметим, что в этой точке функция имеет не просто локальный минимум, но наименьшее значение (глобальный минимум).

ЛЕКЦИЯ 7. ЧИСЛОВЫЕ РЯДЫ И ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.

ТЕМА 11. ЧИСЛОВЫЕ РЯДЫ.

Понятие числового ряда. Знакоположительные ряды и их сходимость. Признаки сходимости рядов. Знакопеременные ряды. Абсолютная и условная сходимость. Функциональные ряды. Степенные ряды. Радиус сходимости.

Понятие числового ряда. Сумма ряда.

Числовым рядом называется бесконечная последовательность чисел , , , , , соединенных знаком сложения: .

Числа , , , , называются членами ряла, а член — общим или -м членом ряда.

Сумма первых членов ряда называется -й частичной суммой ряда.

Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, т. е. . Число называется суммой ряда. В этом смысле можно записать . Если конечного предела последовательности частичных сумм не существует, то ряд называется расходящимся.

Свойства числовых рядов.

1. Если ряд сходится и имеет сумму , то и ряд (полученный умножением данного ряда на число ) также сходится и имеет сумму ,

2. Если ряды и сходятся и их суммы соответственно равны и , то и ряд 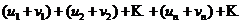(представляющий сумму

данных рядов) также сходится, и его сумма равна .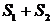

Свойства 1 и 2 непосредственно вытекают из свойств пределов числовых последовательностей.

3. Если ряд сходится, то сходится и ряд, полученный из данного путем отбрасывания (или приписывания) конечного числа членов.

Ряд, полученный из данного отбрасыванием его первых членов, называется -м остатком ряда.

Если сумму -го остатка ряда обозначить через , т. е.

,

то сумму ряда можно представить в виде .

4. Для того чтобы ряд сходился, необходимо и достаточно, чтобы при остаток ряда стремился к нулю, т. е. чтобы .

Это свойство вытекает из теоремы о связи бесконечно малых с пределами функций.

Необходимый признак сходимости ряда.

Теорема (необходимый признак сходимости). Если ряд сходится, то предел его общего члена при равен нулю, т. е. .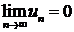

Следствие. Если предел общего члена ряда при не равен нулю, т. е. , то ряд расходится.

Замечание. Следует подчеркнуть, что данная теорема выражает лишь необходимый, но недостаточный признак сходимости ряда. Если , то из этого еще не следует, что ряд сходится. Пример: гармонический ряд . Хотя , гармонический ряд расходится.

Признаки сходимости знакоположительных рядов.

Теорема (признак сравнения). Пусть даны два ряда с положительными членам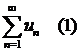и: и 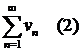, причем члены первого ряда не превосходят членов второго, т. е. при любом . Тогда: а) если сходится ряд 2, то сходится и ряд 1; б) если расходится ряд 1, то расходится и ряд 2.

Отметим «эталонные» ряды, часто используемые для сравнения:

1) геометрический ряд 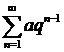— сходится при расходится при ;

2) гармонический ряд расходится;

3) обобщенный гармонический ряд сходится при , расходится при .

Нестандартность применения признака сравнения заключается в том, что надо не только подобрать соответствующий «эталонный» ряд, но и доказать неравенство , для чего часто требуется преобразование рядов (например, отбрасывание или приписывание конечного числа членов, умножение на определенные числа и т. п.). В ряде случаев более простым оказывается предельный признак сравнения.

Теорема (предельный признак сравнения). Если и — ряды с положительными членами и существует конечный предел отношения их общих членов 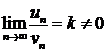, то ряды одновременно сходятся либо расходятся.

Весьма удобным на практике является признак Даламбера.

Теорема (признак Даламбера). Пусть для ряда с положительными членами существует предел отношения -го члена к -му члену 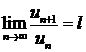. Тогда, если , то ряд сходится; если , то ряд расходится; если , то вопрос о сходимости ряда остается нерешенным.

Теорема (интегральный признак сходимости). Пусть дан ряд члены которого положительны и не возрастают, т. е. , а функция , определенная при , непрерывная и невозрастающая и .

Тогда для сходимости ряда необходимо и достаточно, чтобы сходился несобственный интеграл .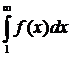

Ряды с членами произвольного знака.

Под знакочередующимся рядом понимается ряд, в котором члены попеременно то положительны, то отрицательны.

Теорема (признак Лейбница). Если члены знакочередующегося ряда убывают по абсолютной величине и предел его общего члена при равен нулю, т. е. , то ряд сходится, а его сумма не превосходит первого члена: .

Следствие. Погрешность при приближенном вычислении суммы сходящегося знакочередующегося ряда, удовлетворяющего условиям теоремы Лейбница, по абсолютной величине не превышает абсолютной величины первого отброшенного члена.

Знакопеременные ряды. Пусть знакопеременный ряд, в котором любой его член может быть как положительным, так и отрицательным.

Теорема (достаточный признак сходимости знакопеременного ряда). Если ряд, составленный из абсолютных величин членов данного ряда, сходится, то сходится и данный ряд.

Ряд называется абсолютно сходящимся, если сходится как сам ряд, так и ряд, составленный из абсолютных величин его членов.

Ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.

Например, ряд 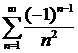— абсолютно сходящийся, а ряд 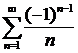— условно сходящийся.

Грубо говоря, различие между абсолютно сходящимися и условно сходящимися рядами заключается в следующем: абсолютно сходящиеся ряды сходятся в основном в силу того, что их члены быстро убывают, а условно сходящиеся — в результате того, что положительные и отрицательные слагаемые уничтожают друг друга.

Свойства абсолютно и условно сходящихся рядов существенно отличаются. Абсолютно сходящиеся ряды по своим свойствам напоминают конечные суммы, их можно складывать, перемножать, переставлять местами члены ряда.

Условно сходящиеся ряды такими свойствами не обладают. Можно показать (теорема Римана), что от перестановки членов условно сходяшегося ряда можно получить ряд, имеющий любую наперед заданную сумму, и даже расходящийся ряд.

Понятие функционального ряда. Область сходимости функционального ряда. Степенные ряды. Теорема Абеля. Интервал и радиус сходимости степенного ряда.

Членами рядов могут являться функции, в частности степенные функции

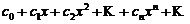
Такие ряды называются степенными, а числа — коэффициентами степенного ряда.

Совокупность тех значений , при которых степенной ряд сходится, называется областью сходимости степенного ряда.

Структура области сходимости степенного ряда устанавливается с помощью теоремы Абеля.

Теорема Абеля. 1) Если степенной ряд сходится при значении (отличном от нуля), то он сходится и, притом абсолютно, при всех значениях таких, что . 2) Если степенной ряд расходится при , то он расходится при всех значениях таких, что .

Из теоремы Абеля следует, что существует такое число , что при ряд сходится, а при — расходится.

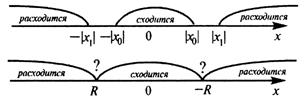
Число получило название радиуса сходимости, а интервал — интервала сходимости степенного ряда. На концах интервала сходимости, т. е. при и , ряд может как сходиться, так и расходиться.

Выражение радиуса сходимости степенного ряда через его коэффициенты: .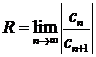

Замечание. Следует отметить, что у некоторых рядов интервал сходимости вырождается в точку , у других охватывает всю ось .

Интегрирование и дифференцирование степенных рядов.

Пусть функция является суммой степенного ряда, т. е. .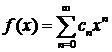

Степенные ряды по своим свойствам напоминают конечные суммы (многочлены):

на любом отрезке , целиком принадлежащем интервалу сходимости , функция является непрерывной, а следовательно, степенной ряд можно почленно интегрировать на этом отрезке:

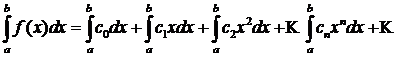
Кроме того, в интервале сходимости степенной ряд можно почленно дифференцировать:

.

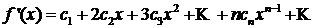При этом после интегрирования или дифференцирования полученные ряды имеют тот же радиус сходимости .

Ряды Тейлора и Маклорена.

Рядом Маклорена для функции называется степенной ряд

.

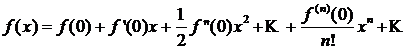Следует отметить, что не все функции могут быть разложены в ряд Маклорена. Может оказаться, что ряд Маклорена, составленный формально для функции , является расходящимся либо сходящимся не к функции .

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9