Математика. Часть 2. Лекция 5. Интегральное исчисление функции одной переменной (стр. 4 )

Так же как и для числовых рядов, сумму ряда Маклорена можно представить в виде , где — -я частичная сумма ряда; — -й остаток

ряда. Тогда на основании свойства 4 сходящихся рядов можно сформулировать теорему.

Теорема. Для того чтобы ряд Маклорена сходился к функции f(x), необходимо и достаточно, чтобы при остаток ряда стремился к нулю, т. е. для всех значений из интервала сходимости ряда.

Можно доказать, что если функция разложима в ряд Маклорена, то это разложение единственное.

Замечание. Ряд Маклорена является частным случаем ряда Тейлора.

Разложение в ряд Маклорена некоторых функций.

1.  Область сходимости ряда .

2. 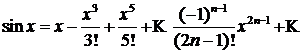 Область сходимости ряда .

3. 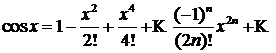 Область сходимости ряда .

4.  Интервал сходимости ряда (на концах интервала при сходимость ряда зависит от конкретных значений ). Данный ряд называется биномиальным. Если — целое положительное число, то биномиальный ряд представляет формулу бинома Ньютона.

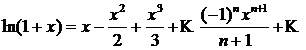Область сходимости ряда (после выяснения сходимости на концах интервала сходимости) есть .

ТЕМА 12. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.

Понятие обыкновенного дифференциального уравнения. Определение решения обыкновенного дифференциального уравнения (задача Коши). Геометрическая интерпретация решения обыкновенного дифференциального уравнения.

Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами.

Основные понятия.

Дифференциальным уравнением называется уравнение, связывающее искомую функцию одной или нескольких переменных, эти переменные и производные различных порядков данной функции. Если искомая функция зависит от одной переменной, то дифференциальное уравнение называется обыкновенным, если от нескольких — то уравнением в частных производных. Мы будем рассматривать только обыкновенные дифференциальные уравнения.

Простейший пример дифференциального уравнения дает задача о нахождении первообразной для заданной функции , поскольку ее можно рассматривать как задачу о нахождении функции, удовлетворяющей уравнению .

В общем случае дифференциальное уравнение можно записать в виде

,

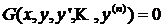где — некоторая функция от переменных, , при этом порядок старшей производной, входящей в запись уравнения, называется порядком дифференциального уравнения.

Дифференциальное уравнение -го порядка называется разрешенным относительно старшей производной, если оно имеет вид

,

где — некоторая функция от переменной.

Решением дифференциального уравнения называется такая функция , которая при подстановке ее в это уравнение обращает его в тождество.

Задача о нахождении решения некоторого дифференциального уравнения называется задачей интегрирования данного дифференциального уравнения. График решения дифференциального уравнения называется интегральной кривой.

Общим решением дифференциального уравнения -го порядка называется такое его решение , которое является функцией переменной и произвольных независимых постоянных . (Независимость постоянных означает отсутствие каких-либо соотношений между ними.)

Частным решением дифференциального уравнения называется решение, получаемое из общего решения при некоторых конкретных числовых значениях постоянных .

Дифференциальные уравнения первого порядка. Теорема о существовании и единственности решения.

Рассмотрим вопросы теории дифференциальных уравнений на примере уравнений первого порядка, разрешенных относительно производной, т. е. таких, которые допускают представление в виде

,

где — некоторая функция двух переменных.

Мы будем обозначать через область определения функции , дополнительно предполагая, что множество является открытым.

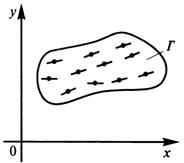
Рассмотрим геометрический смысл уравнения. Производная функции представляет угловой коэффициент (тангенс угла наклона) касательной к кривой в точке с абсциссой . Следовательно, уравнение каждой точке плоскости задает направление касательной к интегральной кривой , проходящей через эту точку. Говорят также, что уравнение задает поле направлений в области .

Решить уравнение — значит найти семейство кривых, отвечающих заданному полю направлений.

Теорема. Пусть в дифференциальном уравнении функция и ее частная производная — непрерывны на открытом множестве координатной плоскости . Тогда:

1. Для всякой точки множества найдется решение уравнения, удовлетворяющее начальному условию ;

2. Если два решения и уравнения совпадают хотя бы для одного значения , т. е. если , то эти решения совпадают для всех тех значений переменной , для которых они определены.

Геометрический смысл теоремы состоит в том, что через каждую точку множества проходит одна и только одна интегральная кривая уравнения.

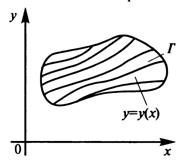
Теорема устанавливает условия существования и единственности решения задачи Коши — задачи отыскания частного решения дифференциального уравнения, удовлетворяющего начальному условию .

Основные типы дифференциальных уравнений первого порядка и методы их решения.

Дифференциальное уравнение первого порядка называется неполным, если функция явно зависит либо только от , либо только от . Рассмотрим решения таких уравнений.

1. Уравнение или . Перепишем уравнение в виде , откуда его решение .

2. Уравнение . Его решение удобно искать в виде , т. е. считать, что

переменная обозначает независимую переменную, а переменная — функцию. В этом случае из получаем 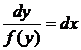и .

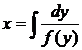Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если оно может быть представлено в виде или в виде

,

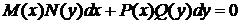где — некоторые функции переменной ; — функции переменной .

Для решения такого уравнения его следует преобразовать к виду, в котором дифференциал и функции переменной окажутся в одной части равенства, а переменной — в другой. Затем проинтегрировать обе части полученного равенства.

Например, 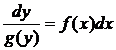и .

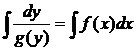Дифференциальное уравнение первого порядка называется однородным, если оно может быть представлено в виде , где — некоторая функция (одной переменной). Например, уравнение 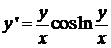— однородное. Понятие однородного дифференциального уравнения связано с однородными функциями. Функция называется однородной степени (по переменным и ), если для произвольного числа выполняется равенство .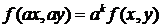

Вспомогательная функция от переменной (замена переменной) позволяет свести это уравнение к уравнению с разделяющимися переменными. Действительно, так как , то , поэтому уравнение приобретает следующий вид, откуда получим, что .

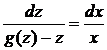Дифференциальное уравнение первого порядка называется линейным, если оно имеет вид

,

где и — некоторые (непрерывные) функции переменной . В случае, когда функция тождественно равна нулю, уравнение называется однородным, в противном случае — неоднородным.

Рассмотрим один из возможных способов решения уравнения : будем искать решение в виде (тем самым искомыми становятся функции и , одна из которых может быть выбрана произвольно, а другая — должна определяться из уравнения. Так как , то из следует или

.

Найдем сначала какое-либо частное решение уравнения

Тогда функция — решение уравнения

Тем самым решение исходного уравнения сводится к решению двух уравнений с разделяющимися переменными (см. и ).

Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Линейное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид

где — некоторые действительные числа, — некоторая функция. Если , то уравнение

называется однородным, в противном случае при уравнение называется неоднородным.

Можно доказать, что существует единственное решение уравнения , удовлетворяющее начальным условиям , , где — некоторые (действительные) числа.

Рассмотрим сначала решение линейного однородного уравнения с постоянными коэффициентами.

Напомним, что линейной комбинацией функций и с коэффициентами и называется выражение вида . Если линейная комбинация функций равна нулевой функции только тогда, когда коэффициенты и равны нулю, то функции и называются линейно независимыми, в противном случае — линейно зависимыми.

Теорема 1. Если и — линейно независимые частные решения уравнения, то общее решение этого уравнения является линейной комбинацией этих частных решений.

Итак, чтобы найти общее решение уравнения, надо знать два его частных решения и . Будем искать решение уравнения в форме

,

где — некоторое (действительное) число (если такое существует). Так как , то функция является решением уравнения, если число есть корень уравнения

,

которое называется характеристическим уравнением исходного уравнения.

Описание решений уравнения зависит от того, имеет ли соответствующее характеристическое уравнение (12.37) два различных корня, один корень или не имеет действительных корней. Справедлива теорема.

Теорема 2. 1. Пусть характеристическое уравнение уравнения имеет действительные корни и , причем . Тогда общее решение уравнения имеет вид , где и — некоторые числа.

2. Если характеристическое уравнение имеет один корень (кратности 2), то общее решение уравнения имеет вид , где и — некоторые числа.

3. Если характеристическое уравнение не имеет действительных корней, то общее решение уравнения имеет вид , где , , и — некоторые числа.

Перейдем теперь к решению линейного неоднородного уравнения с постоянными коэффициентами.

Это уравнение может быть, в частности, решено методом вариации произвольных постоянных, который состоит в следующем. Сначала находится общее решение однородного уравнения, имеющего ту же левую часть, что и исходное неоднородное уравнение. Затем решение уравнения находится в виде , т. е. предполагается, что постоянные и являются функциями независимой переменной . При этом функции и могут быть найдены как решения системы

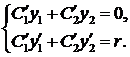
Теорема 3. Общее решение линейного неоднородного дифференциального уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения исходного неоднородного уравнения.

Следует отметить, что метод вариации произвольных постоянных достаточно сложен, поэтому в ряде случаев целесообразно использовать другие методы решения, основанные на теореме 3. Сначала, как и при методе вариации произвольных постоянных, находится общее решение однородного дифференциального уравнения, а затем отыскивается частное решение неоднородного уравнения. При этом вид частного решения устанавливается по виду правой части уравнения, и задача сводится к отысканию коэффициентов этого частного решения.

ЛЕКЦИЯ 8. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА.

ТЕМА 13. ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ.

Случайные события. Достоверное, невозможное, противоположное и равносильное события. Дополнение событий (противоположное событие). Полная группа событий.

Случайные события

Одним из основных понятий теории вероятностей является понятие события.

Случайным событием (возможным событием или просто событием) называется любой факт, который в результате испытания может произойти или не произойти.

Под испытанием (опытом, экспериментом) в этом определении понимается выполнение определенного комплекса условий, в которых наблюдается то или иное явление, фиксируется тот или иной результат.

События обозначаются прописными (заглавными) буквами латинского алфавита: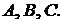

Если при каждом испытании, при котором происходит событие, происходит и событие , то говорят, что влечет за собой событие (входит в , является частным случаем, вариантом ) или включает событие , и обозначают . Например, если событие — изделие 1-го сорта, — изделие 2-го сорта, — изделие стандартное, то и .

Если одновременно и , то в этом случае события и называют равносильными и обозначают . События называются несовместными (несовместимыми), если наступление одного из них исключает наступление любого другого. В противном случае события называются совместными (совместимыми). Событие называется достоверным (обозначаем буквой ), если в результате испытания оно обязательно должно произойти. Событие называется невозможным (обозначаем символом ), если в результате испытания оно вообще не может произойти. События называются равновозможными, если в результате испытания по условиям симметрии ни одно из этих событий не является объективно более возможным.

Несколько событий называются единственно возможными, если в результате испытания обязательно должно произойти хотя бы одно из них. Несколько событий образуют полную группу (полную систему), если они являются единственно возможными и несовместными исходами испытания. Это означает, что в результате испытания обязательно должно произойти одно и только одно из этих событий.

Частным случаем событий, образующих полную группу, являются противоположные события. Два несовместных события, из которых одно должно обязательно произойти, называются противоположными. Событие, противоположное событию , будем обозначать .

Классическое определение вероятности. Сумма (объединение) и произведение (пересечение) событий. Теорема сложения вероятностей. Условная вероятность. Теорема умножения вероятностей. Независимость событий.

Классическое определение вероятности

Численная мера степени объективной возможности наступления события называется вероятностью события. Это определение, качественно отражающее понятие вероятности события, не является математическим. Чтобы оно таким стало, необходимо определить его количественно.

Пусть исходы некоторого испытания образуют полную группу событий и равновозможны, т. е. единственно возможны, несовместны и равновозможны. Такие исходы называются элементарными исходами, случаями или шансами. При этом говорят, что испытание сводится к схеме случаев или «схеме урн» (ибо любую вероятностную задачу для рассматриваемого испытания можно заменить эквивалентной задачей с урнами и шарами разных цветов).

Случай называется благоприятствующим (благоприятным) событию , если появление этого случая влечет за собой появление события . Согласно классическому определению вероятность события равна отношению числа случаев, благоприятствующих ему, к общему числу случаев, т. е.

,

где — вероятность события ; — число случаев, благоприятствующих событию ; — общее число случаев.

Пример. При бросании игральной кости возможны шесть исходов — выпадение 1, 2, 3, 4, 5, 6 очков. Какова вероятность появления четного числа очков?

Решение. Все исходов образуют полную группу событий и равновозможны, т. е. единственно возможны, несовместны и равновозможны. Событию — «появление четного числа очков» благоприятствуют 3 исхода (случая) — 2, 4 и 6 очков. По формуле .

Классическое определение (точнее, классическая формула) вероятности долгое время, с XVII вплоть до XIX в., рассматривалось действительно как определение вероятности, так как в то время методы теории вероятностей применялись в основном к азартным играм, которые сводились к схеме случаев, или в задачах, которые искусственно сводились к этой схеме. В настоящее время формальное определение вероятности не дается (это понятие считается первичным и не определяется, а при его пояснении используют понятие относительной частоты события).

Поэтому классическое определение (классическую формулу) вероятности следует рассматривать не как определение, а как метод вычисления вероятностей для испытаний, сводящихся к схеме случаев.

Отметим свойства вероятности события.

1. Вероятность любого события заключена между нулем и единицей, т. е.

2. Вероятность достоверного события равна единице, т. е.

3. Вероятность невозможного события равна нулю, т. е.

.

События, вероятности которых очень малы (близки к нулю) или очень велики (близки к единице), называются соответственно практически невозможными или практически достоверными событиями.

Элементы комбинаторики

Для успешного решения задач с использованием классического определения вероятности необходимо знать основные правила и формулы комбинаторики — раздела математики, изучающего, в частности, методы решения комбинаторных задач — задач на подсчет числа различных комбинаций.

Если комбинации из элементов по отличаются только составом элементов, то их называют сочетаниями из элементов по . Число сочетаний из элементов по равно

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9