.

Обращаем внимание на то, что дисперсия как суммы, так и разности независимых случайных величин и равна сумме их дисперсий, т. е. .

Математическое ожидание, дисперсия, среднее квадратическое отклонение и другие числа, призванные в сжатой форме выразить наиболее существенные черты распределения, называются числовыми характеристиками случайной величины.

Обращаем внимание на то, что сама величина — случайная, а ее числовые характеристики являются величинами неслучайными, постоянными.

В теории вероятностей числовые характеристики играют большую роль. Часто удается решать вероятностные задачи, оперируя лишь числовыми характеристиками случайных

величин. Применение вероятностных методов для решения практических задач в значительной мере определяется умением пользоваться числовыми характеристиками случайной величины, оставляя в стороне законы распределения.

Понятие математического ожидания и дисперсии можно распространить на непрерывные случайные величины.

Для получения соответствующих формул для и достаточно в формулах и для дискретной случайной величины заменить знак суммирования по всем ее значениям знаком интеграла с бесконечными пределами, «скачущий» аргумент — непрерывно меняющимся , а вероятность — элементом вероятности . Под элементом вероятности понимается вероятность попадания случайной величины на участок 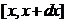(с точностью до бесконечно малых более высоких порядков); геометрически элемент вероятности приближенно равен площади элементарного прямоугольника, опирающегося на отрезок .

В результате получим следующие формулы для математического ожидания и дисперсии непрерывной случайной величины :

(если интеграл абсолютно сходится) и

(если интеграл сходится).

На практике обычно область значений случайной величины, для которых , ограничена и указанные интегралы сходятся, а значит, существуют и .

Все свойства математического ожидания и дисперсии, рассмотренные выше для дискретных случайных величин, справедливы и для непрерывных величин.

Биномиальное распределение, распределение Пуассона.

Показательное распределение. Равномерное распределение. Нормальный закон распределения.

Формула Бернулли

На практике часто приходится сталкиваться с задачами, которые можно представить в виде многократно повторяющихся испытаний при данном комплексе условий, в которых представляет интерес вероятность числа наступлений некоторого события в испытаниях. Например, необходимо определить вероятность определенного числа попаданий в мишень при нескольких выстрелах, вероятность некоторого числа бракованных изделий в данной партии и т. д.

Если вероятность наступления события в каждом испытании не меняется в зависимости от исходов других, то такие испытания называются независимыми относительно события . Если независимые повторные испытания проводятся при одном и том же комплексе условий, то вероятность наступления события в каждом испытании одна и та же. Описанная последовательность независимых испытаний получила название схемы Бернулли.

Теорема. Если вероятность наступления события в каждом испытании постоянна, то вероятность того, что событие наступит раз в независимых испытаниях, равна

,

где .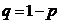

Пример. Вероятность изготовления на автоматическом станке стандартной детали равна 0,8. Найти вероятности возможного числа появления бракованных деталей среди 5 отобранных.

Решение. Вероятность изготовления бракованной детали . Искомые вероятности находим по формуле Бернулли :

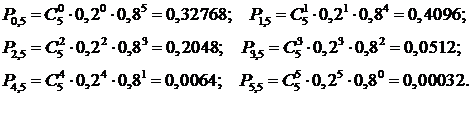
Полученные вероятности изобразим графически точками с координатами . Соединяя эти точки, получим многоугольник, или полигон, распределения вероятностей.

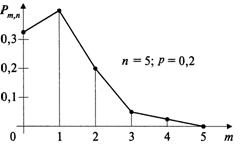
Рассматривая многоугольник распределения вероятностей, видим, что есть такие значения (в данном случае, одно — ), обладающие наибольшей вероятностью .

Число наступления события в независимых испытаниях называется наивероятнейшим, если вероятность осуществления этого события по крайней мере не меньше вероятностей других событий при любом .

Для нахождения запишем систему неравенств:

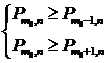
Решение дается двойным неравенством:

Отметим, что так как разность , то всегда существует целое число , удовлетворяющее неравенству. При этом, если 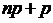— целое число, то наивероятнейших чисел два: и .

Биномиальное распределение

Дискретная случайная величина имеет биномиальный закон распределения с параметрами и , если она принимает значения с вероятностями

,

где .

Как видим, вероятности находятся по формуле Бернулли. Следовательно, биномиальный закон распределения представляет собой закон распределения числа наступлений события в независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью .

Ряд распределения биномиального закона имеет вид:

Очевидно, что определение биномиального закона корректно, так как основное свойство ряда распределения 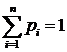выполнено, ибо есть не что иное, как сумма всех членов разложения бинома Ньютона:

(отсюда и название закона — биномиальный).

Теорема. Математическое ожидание случайной величины , распределенной по биномиальному закону,

,

а ее дисперсия

Биномиальный закон распределения широко используется в теории и практике статистического контроля качества продукции, при описании функционирования систем массового обслуживания, при моделировании цен активов, в теории стрельбы и в других областях.

Формула Пуассона

Предположим, что мы хотим вычислить вероятность появления события при большом числе испытаний , например, . По формуле Бернулли

.

Ясно, что в этом случае непосредственное вычисление по формуле Бернулли технически сложно, тем более если учесть, что сами и — числа дробные. Поэтому возникает естественное желание иметь более простые приближенные формулы для вычисления при больших . Такие формулы, называемые асимптотическими, существуют и определяются теоремой Пуассона, локальной и интегральной теоремами Муавра—Лапласа.

Наиболее простой из них является теорема Пуассона.

Теорема. Если вероятность наступления события в каждом испытании стремится к нулю () при неограниченном увеличении числа испытаний (), причем произведение стремится к постоянному числу , то вероятность того, что событие появится раз в независимых испытаниях, удовлетворяет предельному равенству

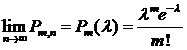
Строго говоря, условие теоремы Пуассона при , так что , противоречит исходной предпосылке схемы испытаний Бернулли, согласно которой вероятность наступления события в каждом испытании . Однако, если вероятность — постоянна и мала, число испытаний — велико и число — незначительно (будем полагать, что ), то из предельного равенства вытекает приближенная формула Пуассона:

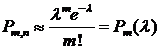
Распределение Пуассона

Дискретная случайная величина имеет закон распределения Пуассона с параметром , если она принимает значения (бесконечное, но счетное множество значений) с вероятностями

Ряд распределения закона Пуассона имеет вид:

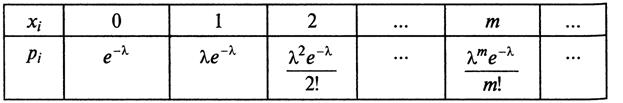
Очевидно, что определение закона Пуассона корректно, так как основное свойство ряда распределения 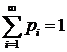выполнено, ибо сумма ряда

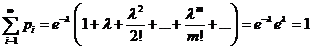
(учтено, что в скобках записано разложение в ряд функции при ).

На рисунке показан многоугольник (полигон) распределения случайной величины,

распределенной по закону Пуассона с параметрами .

Теорема. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру этого закона, т. е.

,

.

При достаточно больших (вообще при ) и малых значениях () при условии, что произведение — постоянная величина (), закон распределения Пуассона является хорошим приближением биномиального закона, так как в этом случае функция вероятностей Пуассона хорошо аппроксимирует функцию вероятностей, определяемую по формуле Бернулли. Иначе, при , , закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность события в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.

По закону Пуассона распределены, например, число рождения четверней, число сбоев на автоматической линии, число отказов сложной системы в «нормальном режиме», число

«требований на обслуживание», поступивших в единицу времени в системах массового обслуживания, и др.

Показательное распределение

Непрерывная случайная величина имеет показательный (экспоненциальный) закон распределения с параметром , если ее плотность вероятности имеет вид:

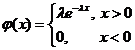
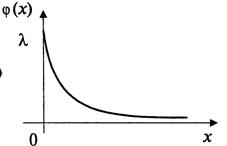
Кривая распределения и график функции распределения случайной величины приведены на следующих рисунках.

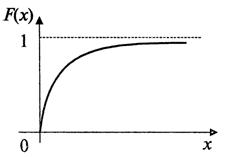
Теорема. Функция распределения случайной величины , распределенной по показательному (экспоненциальному) закону, есть

,

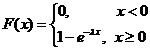ее математическое ожидание

,

а дисперсия

.

Из данной теоремы следует, что для случайной величины, распределенной по показательному закону, математическое ожидание равно среднему квадратическому отклонению, т. е.

.

Показательный закон распределения играет большую роль в теории массового обслуживания и теории надежности.

Равномерное распределение

Непрерывная случайная величина имеет равномерный закон распределения на отрезке , если ее плотность вероятности постоянна на этом отрезке и равна нулю вне его, т. е.

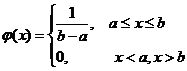
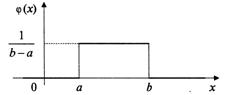
Кривая распределения и график функции распределения случайной величины приведены на следующих рисунках.

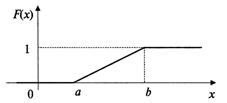
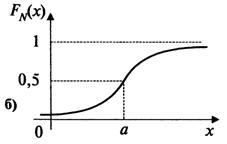
Теорема. Функция распределения случайной величины , распределенной по равномерному закону, есть

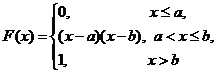
ее математическое ожидание

а дисперсия

.

Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчетов (например, ошибка округления числа до целого распределена равномерно на отрезке [—0,5; +0,5]), в ряде задач массового обслуживания, при статистическом моделировании наблюдений, подчиненных заданному распределению. Так, случайная величина , распределенная по равномерному закону на отрезке [0;1], «называемая случайным числом от 0 до 1», служит исходным материалом для получения случайных величин с любым законом распределения.

Нормальный закон распределения

Нормальный закон распределения наиболее часто встречается на практике. Главная особенность, выделяющая его среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях.

Непрерывная случайная величина имеет нормальный закон распределения (закон Гаусса) с параметрами и , если ее плотность вероятности имеет вид:

.

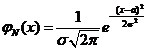Термин «нормальный» не совсем удачный. Многие признаки подчиняются нормальному закону, например, рост человека, дальность полета снаряда и т. п. Но если какой-либо признак подчиняется другому, отличному от нормального, закону распределения, то это вовсе не говорит о «ненормальности» явления, связанного с этим признаком.

Кривую нормального закона распределения называют нормальной или гауссовой кривой. На рисунке приведены нормальная кривая с параметрами и , т. е. , и график функции распределения случайной величины , имеющей нормальный закон.

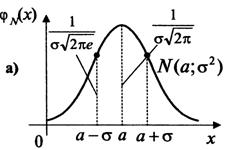
Обратим внимание на то, что нормальная кривая симметрична относительно прямой , имеет максимум в точке , равный , т. е. ,

и две точки перегиба с ординатой .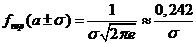

Можно заметить, что в выражении плотности нормального закона параметры обозначены буквами и , которыми мы обозначаем математическое ожидание и дисперсию .

Такое совпадение неслучайно. Рассмотрим теорему, устанавливающую теоретико-вероятностный смысл параметров нормального закона.

Теорема. Математическое ожидание случайной величины , распределенной по нормальному закону, равно параметру этого закона, т. е.

,

а ее дисперсия — параметру , т. е.

.

Выясним, как будет меняться нормальная кривая при изменении параметров и .

Параметр (он же математическое ожидание) характеризует положение центра, а параметр (он же дисперсия) — форму нормальной кривой.

Нормальный закон распределения случайной величины с параметрами , , т. е. , называется стандартным или нормированным, а соответствующая нормальная кривая — стандартной или нормированной.

Сложность непосредственного нахождения функции распределения случайной величины, распределенной по нормальному закону, связана с тем, что интеграл от функции является «неберущимся» в элементарных функциях. Поэтому их выражают через функцию

— функцию (интеграл вероятностей) Лапласа, для которой составлены таблицы.

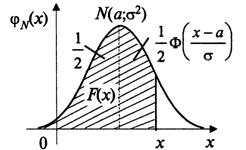
Теорема. Функция распределения случайной величины , распределенной по нормальному закону, выражается через функцию Лапласа по формуле:

.

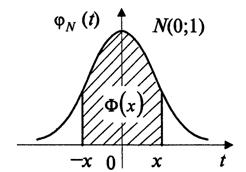
Геометрически функция распределения представляет собой площадь под нормальной кривой на интервале . Она состоит из двух частей: первой, на интервале , равной 1/2, т. е. половине всей площади под нормальной кривой, и второй, на интервале , равной .

Рассмотрим свойства случайной величины, распределенной по нормальному закону.

1. Вероятность попадания случайной величины , распределенной по нормальному закону, в интервал , равна

,

где .

2. Вероятность того, что отклонение случайной величины , распределенной по нормальному закону, от математического ожидания не превысит величину (по абсолютной величине), равна

,

где .

Вычислим по формуле вероятности при различных значениях .

Отсюда вытекает «правило трех сигм»:

Если случайная величина X имеет нормальный закон распределения с параметрами и , т. е. , то практически достоверно, что ее значения заключены в интервале .

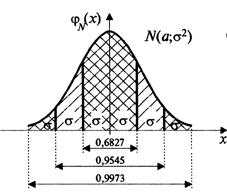
Нарушение «правила трех сигм», т. е. отклонение нормально распределенной случайной величины больше, чем на (по абсолютной величине), является событием практически невозможным, так как его вероятность весьма мала:

.

Найдем коэффициент асимметрии и эксцесс случайной величины , распределенной по нормальному закону.

Очевидно, в силу симметрии нормальной кривой относительно вертикальной прямой , проходящей через центр распределения коэффициент асимметрии нормального

распределения .

Эксцесс нормально распределенной случайной величины

,

где учли, что центральный момент 4-го порядка

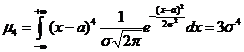
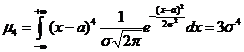
(вычисление интеграла опускаем).

Таким образом, эксцесс нормального распределения равен нулю, и крутость других распределений определяется по отношению к нормальному.

В силу особенностей нормального закона распределения, он занимает центральное место в теории и практике вероятностно-статистических методов. Большое теоретическое значение нормального закона состоит в том, что с его помощью получен ряд важных распределений.

Закон больших чисел и предельные теоремы. Понятие о предельной теореме Ляпунова.

Под законом больших чисел в широком смысле понимается общий принцип, согласно которому, по формулировке академика , совокупное действие большого числа случайных факторов приводит (при некоторых весьма общих условиях) к результату, почти не зависящему от случая. Другими словами, при большом числе случайных величин их средний результат перестает быть случайным и может быть предсказан с большой степенью определенности.

Под законом больших чисел в узком смысле понимается ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9