4). Оценку досрочной утраты трудоспособности работников профессиональных групп с высокими и запретительно-высокими уровнями риска, направляемых в комиссии медико-социальной экспертизы утраты трудоспособности с диагнозом «подозрение на профессиональное заболевание» и «профессиональное заболевание», на основе методов углубленных периодических медицинских осмотров (индивидуальный метод оценки риска).

Другими словами: наиболее оптимальным вариантом применения вышеприведенных методов оценки факторов профессионального риска является их одновременное использование, что позволит на основе присущих им взаимодополняющих качеств более объективно оценивать профессиональные риски и создать развитую инфраструктуру регистрации факторов риска, мониторинга накопленной дозы и состояния здоровья и трудоспособности работников.

Таким образом, оценка профессионального риска на основе аттестации рабочих мест является ориентировочной и ее следует подкреплять второй составляющей – гигиенической оценкой состояния условий труда, а также третьей составляющей – показателями индивидуально накопленной дозы воздействия опасных и вредных производственных факторов, а также оценки уровней профессиональной и производственно-обусловленной заболеваемости и постоянной утратой трудоспособности (четвертая составляющая).

1.5. Построение страховой математической модели оценки профессиональных рисков

В качестве численной характеристикой доли утраченного здоровья или трудоспособности рассмотрим число из отрезка [0, 1] (нуль соответствует абсолютно здоровому человеку, а единица – полной потере здоровья). Некоторое значение , , этой характеристики отвечает такой степени потери трудоспособности, при которой приходится переводить работника на менее вредное производство. Так как измерения доли утраченной трудоспособности во многом носят субъективный характер, то принятие решения о переводе работника на менее вредное производство или инвалидность является случайным, и вероятность принятия такого решения монотонно зависит от реальной доли Z утраченной трудоспособности.

Процесс ухудшения здоровья и утраты трудоспособности человека, работающего на производствах с вредными и/или опасными условиями труда, можно описывать разными способами, из которых далее рассматриваются два вида: детерминированная последовательность чисел из отрезка [0,1] и цепь Маркова с дискретным временем, множеством состояний которой является совокупность чисел от 0 до 1.

Чтобы учитывать ситуации, когда ухудшение состояния здоровья приводит (по случайным причинам) либо к инвалидности или смерти работника, либо к необходимости его перевода на работу с менее вредными условиями и выплаты в связи с этим периодической компенсации потери заработка вплоть до выхода на досрочную пенсию, имеет смысл дополнить величину Z, характеризующую состояние здоровья, дискретной компонентой, определяющей состояние работника: остается он на основном (вредном) производстве, переведен ли на менее вредное производство, переведен на пенсию по инвалидности и т. п. Параметры такой модели зависят от характера производства и выбираются в соответствии с имеющимися статистическими данными.

Изменения численной характеристики здоровья как в детерминистической, так и в вероятностной моделях должны отражать следующие особенности:

а) доля утраченного здоровья естественно увеличивается с возрастом;

б) характер вредных/опасных условий труда определяет специфическую совокупность накапливающихся повреждений организма и характерный для каждого вида производства уровень утраты здоровья за заданное время работы, обусловленный условиями труда (без учета ситуаций полной потери трудоспособности);

в) при малой доле утраченного здоровья восстановительные и компенсационные возможности организма велики, и утрата здоровья и работоспособности происходит медленнее, чем при умеренной доле утраченного здоровья;

г) если характер вредных воздействий условий труда существенно влияет лишь на часть подсистем организма, то при приближении к предельному для данного производства уровню скорость увеличения утраты здоровья уменьшается; аналогично, процесс утраты здоровья может также замедляться к старости в связи с замедлением всех процессов в организме;

д) вероятность наступления инвалидности и/или необходимости перевода на работу с пониженным уровнем вредности условий труда возрастает с увеличением доли утраты здоровья.

Введем следующие обозначения:

Zt – числовая характеристика доли утраченной трудоспособности после t лет работы при вредных и/или опасных условиях (как отмечалось, 0 £ Zt £ 1),

b – естественный уровень утраты трудоспособности за год в связи с увеличением возраста, обусловливающий среднюю утрату трудоспособ­ности около 35% к моменту выхода на пенсию по старости в 55–60 лет,

p – степень утраты трудоспособности за год, обуслов­ленный вредными/опасными условиями труда.

Обозначим также через qперев(t) и qвых(t) соответственно вероятности того, что в течение года работник, у которого стаж работы с вредными/опасными условиями труда равен t, в связи с ухудшением состояния здоровья будет переведен на менее вредную работу (и возникнет необходимость в расходовании средств страхового фонда на компенсацию потери заработка) или что он получит право на пенсию по инвалидности или умрет (в обоих случаях он выходит из системы рассматриваемого вида страхования).

В модели выбрана прямая зависимость этих вероятностей от стажа работы, а не от уровня утраты трудоспособности. Такой подход исключает неизбежную субъективность в определении уровня утраты трудоспособности и упрощает оценку этих параметров по статистическим данным. Динамику параметров qперев(t) и qвых(t) можно использовать для обнаружения существенных изменений в уровне вредности/опасности условий труда.

Можно построить много различных математических моделей, в той или иной мере соответствующих описанным выше особенностям процесса утраты здоровья. Ниже описаны две: детерминистическая и вероятностная.

В обеих моделях предполагается, что существует объективный уровень Wt повреждений подсистем организма за t лет работы при вредных условиях труда. Величина Wt ежегодно увеличивается в соответствии с интенсивностями b и p, но медицинские измерения Zt последствий этих повреждений описываются нелинейной функцией h(x), которая принимает значения из отрезка [0, 1] и медленно растет при малых и больших уровнях повреждений: Zt = h(Wt).

Чтобы учесть отмеченное выше замедление влияния вредных/опасных условий труда на трудоспособность Zt, влияние параметра p компенсируется коэффициентом, уменьшающимся при увеличении стажа работы на производстве с вредными/опасными условиями труда. В качестве такого коэффициента в модели выбрана функция max{0,1 – t/T}, где t – стаж работы на производстве с вредными/опасными условиями труда, а T – величина, которая не меньше максимально возможного времени работы при таких условиях. Иначе говоря, средний уровень влияния вредных/опасных условий труда на величину Wt на t-м году стажа считается в модели равным (1 – t/T) p при t < T и равным 0 при t ≥ T.

В детерминистической модели уравнения в этом случае принимают вид

Zt = h(Vt), Vt+1 = Vt + b + p (0,1 – t/T), t =0,1,…T. (1.1)

Выбирая подходящий аналитический вид функции h(x) и значения параметров b, p и T, можно получать желаемый вид зависимости величины Zt от параметра t.

Так, по статистическим данным, приближенные оценки уровня трудоспособности в зависимости от возраста и условий труда имеют следующий вид (см. Табл. 1):

Таблица 1

Зависимость уровня трудоспособности (значения 1 – Z) от возраста и условий труда[19]

Численные расчеты показали, что близкие результаты получаются в математической модели при нелинейной функции

, (1.2)

T = 40, b = 0,018 и p = 0 для благоприятных условий труда:

Vtблаг = 0,018 max(0,t – 25), Ztблаг = h(Vtблаг)

(предполагается, что в 25 лет человек практически здоров), p = 0,009 для списка № 2:

Vt(2) = Vwблаг + 0,018 max(0,t – 25) + 0,009 t(1 – t/(2T)), Zt(2) = h(Vt(2)),

где w – возраст поступления на работу с вредными/опасными условиями тркда, и p = 0,014 для списка № 1:

Vt(1) = Vwблаг + 0,018 max(0,t – 25) + 0,0014 t(1 – t/(2T)), Zt(1) = h(Vt(1)),

Графики функции Zt при этих значениях параметров приведены ниже на рис. 2.

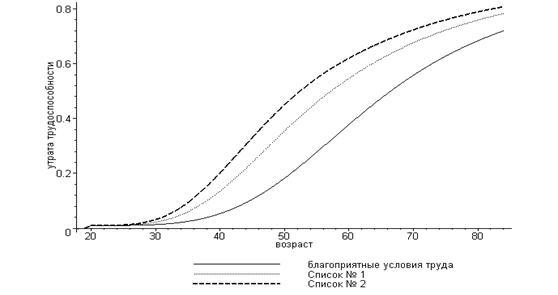
Рис. 2. Зависимость утраты трудоспособности от возраста и условий труда в математической модели.

Численные значения функций Zt при этих параметрах, соответствующие таблице 1, приведены в таблице 2.

Таблица 2

Зависимость уровня утраты трудоспособности (значения Zt) от возраста и условий труда в математической модели

Формулы для кусочно-линейных приближений функций, изображенных на Рис. 2 и в таблице 2, имеют следующий вид (см. Табл. 3):

Таблица 3

Приближенные формулы для зависимости уровня утраты трудоспособности (значения Zt) от возраста и условий труда в математической модели при начале работы в 20 лет

Возраст t	Условия труда
Благоприятные	Список № 2	Список № 1
От 20 до 30	0,004	0,004+0,005(t–20)	0,004+0,01(t–20)
От 30 до 45	0,004+0,006(t–30)	0,054+0,015(t–30)	0,104+0,021(t–30)
От 45 до 60	0,094+0,013(t–45)	0,279+0,008(t–45)	0,419+0,001(t–45)

Аналогичные формулы для уровня утраты трудоспособности в зависимости от стажа и класса условий труда имеют похожий аналитический вид, но параметры подбираются в соответствии со статистическими данными[20], согласно, которым, степени утраты трудоспособности после 30 лет занятости составляют:

для класса %

для класса %

для класса %

для класса 4 40-50%

Параметры модели (1) – (2), соответствующие этим данным, приведены в таблице 4:

Таблица 4

Класс условий труда	b	p	T
3.2	0,018	0,005	40
3.3	0,018	0,008	40
3.4	0,018	0,010	40
4	0,018	0,016	40

Значениям параметров из этой таблицы соответствуют формулы

Vt(3.2) = 0,018 max(0,w + t – 25) + 0,005 t (1 – t/(2T)), Zt(3.2) = h(Vt(3.2)),

Vt(3.3) = 0,018 max(0,w + t – 25) + 0,008 t (1 – t/(2T)), Zt(3.3) = h(Vt(3.3)),

Vt(3.4) = 0,018 max(0,w + t – 25) + 0,01 t (1 – t/(2T)), Zt(3.4) = h(Vt(3.4)),

Vt(4) = Vwблаг + 0,018 max(0, w + t – 25) + 0,016 t (1 – t/(2T)), Zt(4) = h(Vt(4)),

Графики функций Zt, соответствующих таким значениям параметров, приведены на рис. 3.

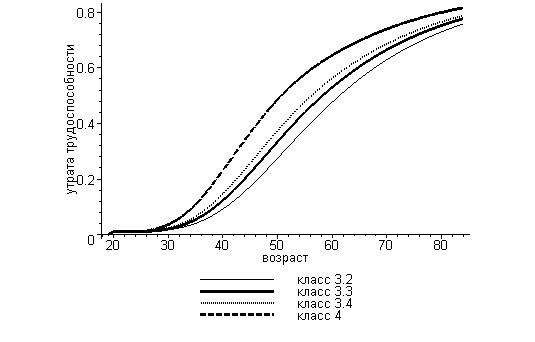
Рис. 3. Зависимость утраты трудоспособности от возраста и классов условий труда в математической модели.

Аналогичные приближенные формулы для различных классов условий труда приведены в Таблице 5.

Таблица 5

Приближенные формулы для зависимости уровня утраты трудоспособности (значения Zt) от возраста и классов условий труда в математической модели при начале работы в 20 лет

Возраст t	Классы условий труда
3.2	3.3	3.4
От 20 до 30	0,004+0,001(t–20)	0,004+0,002(t–20)	0,004+0,004(t–20)
От 30 до 45	0,014+0,010(t–30)	0,024+0,014(t–30)	0,044+0,016(t–30)
От 45 до 55	0,164+0,012(t–45)	0,234+0,008(t–45)	0,284+0,006(t–45)
	4
От 20 до 27	0,004+0,006(t–20)
От 27 до 35	0,046+0,012(t–27)
От 35 до 50	0,142+0,013(t–35)

В аналогичной вероятностной модели

Zt = h(Vt), Vt+1 = Vt + bt + pt max{0,1 – t/T}, (1.3)

функция h имеет тот же вид (1.2), но коэффициенты bt и pt (t = 0,1,…) являются независимыми случайными величинами отражающими влияние увеличения возраста, условий жизни и вредных/опасных условий труда. Распределения bt и pt можно выбирать, исходя из статистических данных и естественных предположений. В частности, математические ожидания bt и pt должны соответствовать значениям параметров b и p в детерминистической модели, а дисперсии соответствовать статистическим данным и априорным соображениям. Тогда и характеристики утраты здоровья Vt и Zt становятся случайными величинами. Случайные величины Vt представляют собой суммы независимых случайных величин, и их распределения можно вычислять с помощью стандартных методов теории вероятностей, а распределения Zt получаются из распределений Vt функциональными преобразованиями.

В этой модели моментом τ наступления страхового события – перевода абстрактного работника на работу с меньшим уровнем вредности или получения права на досрочную пенсию – является наименьшее целочисленное значение аргумента , при котором значение Zt превышает заданный критический уровень .

Глава 2. Актуарное обоснование методов расчетов тарифов, принимая допущение, при котором тарифы должны зависеть от времени работы застрахованных во вредных и опасных условиях труда и периодов получения страхового обеспечения, предполагая, что страховые выплаты будут производиться при потере (снижении) заработка вследствие утраты профессиональной трудоспособности, в том числе досрочной, наступлении профессионального заболевания

2.1. Место и роль страхования досрочной утраты профессиональной трудоспособности в системе социального страхования профессиональных рисков

С позиций социального страхования профессиональный риск означает вероятность наступления для данной профессиональной группы работающих страховых событий, которые будут сопровождаться нарушением здоровья и утратой трудоспособности, а значит и потерей заработков.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10