МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ

ДЕПАРТАМЕНТ КАДРОВОЙ ПОЛИТИКИ И ОБРАЗОВАНИЯ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

СТАВРОПОЛЬСКИЙ ГОСУДАРСТВЕННЫЙ

АГРАРНЫЙ УНИВЕРСИТЕТ

, ,

ЛАБОРАТОРНЫЙ ПРАКТИКУМ

по механике и молекулярной

физике

Учебное пособие для студентов, обучающихся по направлениям:

110800.62 – Агроинженерия, профиль – «Механизация АПК» (бакалавр техники

и технологии), 190100.62 – Наземные транспортно-технологические комплексы (бакалавр техники и технологии), 190600.62 – Эксплуатация транспортно-технологических машин

и комплексов (бакалавр техники и технологии), 221700.62 – Стандартизация и метрология

(бакалавр техники и технологии), 110800.68 – Агроинженерия, программа «Технологии

и средства механизации в сельском хозяйстве» (магистр техники и технологии).

СТАВРОПОЛЬ

2011

УДК 53 (076.5)

ББК 22.36 я 7

С 773

Рецензенты:

Кандидат технических наук, профессор кафедры Машин и технологий

в животноводстве СтГАУ

Доктор технических наук, профессор кафедры Теории механизмов

и деталей машин СтГАУ

Печатается по рекомендации методической комиссии

факультета Механизации сельского хозяйства СтГАУ

(протокол № 5 от 4.04. 2011 г.)

, , . Лабораторный практикум по механике и молекулярной физике. Учебное пособие для студентов аграрных вузов, обучающихся по направлениям: 110800.62 – Агроинженерия, профиль –

«Механизация АПК» (бакалавр техники и технологии), 190100.62 – Наземные транспортно-технологические комплексы (бакалавр техники и технологии), 190600.62 – Эксплуатация транспортно-технологических машин и комплексов (бакалавр техники и технологии), 221700.62 – Стандартизация и метрология (бакалавр техники и технологии), 110800.68 – Агроинженерия, программа «Технологии и средства механизации в сельском хозяйстве» (магистр техники и технологии) – Ставрополь, 2011- 59 с.

В пособии даны указания к выполнению девяти лабораторных работ по разделу «Механика и молекулярная физика» с кратким изложением теоретического материала. Минимально необходимые сведения из математики, а также значения некоторых физических величин приведены в приложениях. Пособие предназначено для студентов аграрных вузов, обучающихся по направлениям: 110800.62 – Агроинженерия, профиль – «Механизация АПК» (бакалавр техники и технологии), 190100.62 – Наземные транспортно-технологические комплексы (бакалавр техники и технологии), 190600.62 – Эксплуатация транспортно-технологических машин и комплексов (бакалавр техники и технологии), 221700.62 – Стандартизация и метрология (бакалавр техники и технологии), 110800.68 – Агроинженерия, программа «Технологии и средства механизации в сельском хозяйстве» (магистр техники и технологии). Может быть использовано в качестве учебного пособия студентами, обучающимися на других инженерных специальностях аграрных вузов.

УДК 53 (076.5)

ББК 22.36 я 7

С 773

© , , 2011

ВВЕДЕНИЕ

Данный практикум включает в себя 9 лабораторных работ по механике и молекулярной физике, отвечающих требованиям Государственного образовательного стандарта и рабочих программ для инженерных факультетов аграрных вузов.

К каждой работе даны: краткая теория по исследуемому физическому явлению; рисунок или схема, описание приборов, установок; порядок выполнения и оформления работы; литература.

Большинство лабораторных работ носит исследовательский характер. В них включены контрольные вопросы, справочные материалы и таблицы, необходимые для выполнения лабораторных работ.

Введение содержит элементы теории погрешностей, примеры вычисления погрешностей при прямых и косвенных измерениях и описание методики проведения измерений с использованием основных измерительных приборов.

Перед выполнением лабораторной работы студент должен предварительно подготовиться к ней, используя данное руководство, записать в тетрадь название работы, цель работы, краткую теорию, основные рабочие формулы и оформить таблицы результатов измерений и вычислений. Также необходимо ответить на контрольные вопросы, используя рекомендуемую литературу

В аудитории, получив допуск к работе, студент должен провести опыты, по полученным данным рассчитать требуемые величины, погрешности измерений, заполнить таблицы, построить графики и сделать выводы.

ТЕОРИЯ ПОГРЕШНОСТЕЙ

Погрешности измерений

Для того чтобы измерить какую-либо величину, нужно определить, сколько раз в ней укладывается однородная величина, принятая за единицу меры. Измерения называют­ся прямыми, если измеряемая величина непосредственно сравнивается с эталоном меры (измерение длины, времени, массы и т. д.). Чаще производят не прямые измерения данной величины, а косвенные - через другие величины, связанные с измеряемой физической ве­личиной определенной зависимостью.

Например, плотность тела определяют по измерениям массы и объема.

Измерительные приборы и наши органы чувств несовершенны. Поэтому все изме­рения можно делать только с определенной степенью точности.

Погрешности, допускаемые во время измерений, делятся на две категории: систе­матические и случайные.

Систематические погрешности - погрешности, связанные с ограниченной точностью изготовления прибора (неравноплечность коромысла весов), неточностью самого метода измерения (пренебрежение силами сопротивления и трения), неправильной установкой прибора (например, сбит нуль шкалы прибора), но эти погрешности в принципе можно исключить, введя соответствующие поправки. Для этого приходится производить поверку приборов по эталонным.

Случайные погрешности - вызываются большим числом случайных при­чин, действие которых на результат каждого измерения различно, и которые не могут быть заранее учтены.

Случайные погрешности могут быть вызваны случайными сотрясениями здания, влиянием незначительного движения воздуха, трением подвижных элементов приборов и могут переноситься в разной мере и с разным знаком из опыта в опыт. Математическая теория случайных величин (статистика) позволяет уменьшить влияние этих погрешностей на конечный результат и установить погрешность измерений. Для этого необходимо про­вести не одно измерение, а несколько. Теория ошибок дает возможность выбрать разум­ное число измерений для обеспечения данной точности.

Погрешность при прямых измерениях

Для уменьшения погрешностей случайного характера измерение данной величины x выполняют многократно (3, 5 и более раз) и получают ряд

значений - х, х2, х3….,хn

1.  Среднеарифметическая величина <х>

<х>= ( х1+ х2+ ……+хn ) = ,

(где n - число измерений) есть величина наиболее близкая к истинному

значению.

2. Абсолютная погрешность измерения отдельных измерений

есть разность между измеренным и средним значением искомой величины

∆xi = xi - <x>

3. Средняя абсолютная погрешность

является единой мерой случайных ошибок всей серии измерений.

4. Средняя относительная погрешность результата измерений есть отношение средней абсолютной погрешности к среднему или табличному значению этой величины

ε = ∙100% или ε=

Как правило, относительные погрешности выражаются в процентах.

Истинное значение измеряемой величины заключено в интервале

X=<X>∆X

Если точность прибора такова, что при любом числе измерений получается одно и то же число, лежащее где-то между делениями шкалы, то приведенный метод оценки по­грешностей неприемлем. В этом случае измерение проводится один раз, в качестве сред­него значения величины X берется среднее арифметическое двух соседних делений шка­лы, между которыми заключено показание прибора, а Δx определяется как половина цены деления шкалы.

Например, высоту цилиндра измеряем штангенциркулем. Цена деления нониуса 0,1 мм.

Средняя абсолютная ошибка, допускаемая при прямых измерениях длины бу­дет равна

∆l = мм = 0,05мм = 5 ∙ 10-5 м

Погрешность при косвенных измерениях

При косвенных измерениях точность выполнения серии опытов ограничивается погрешностями, допущенными при прямых измерениях, входящих в расчетную формулу.

Пусть искомая величина А задана соотношением

A = f ( x, y, z ),

где: х, у, z - независимые величины. Тогда за экспериментальное значение величины А принимают значение

<A>=f ( <x>,<y>,<z> ),

cовпадающее при достаточно малых погрешностях величины А с ее средним значением. Расчет погрешностей при косвенном измерении нельзя произвести так, как при прямом измерении. Ниже приводятся выражения, по которым производятся вычисления относительных ошибок для наиболее часто встречающихся расчетных формул.

1. A = x + y ε = 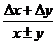∙ 100%

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11