(рис. 1, б).

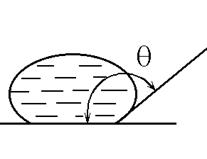
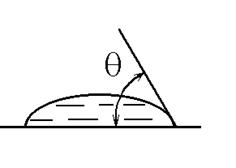
Угол между поверхностью твердого тела и касательной к поверхности жидкости называется краевым углом смачивания q.

Поверхность жидкости (мениск), налитой в сосуд, искривляется у ее стенок: приподнимается в случае смачивающей жидкости (мениск вогнутый – рис. 2, а) и опускается в случае несмачивающей жидкости (мениск выпуклый – рис. 2, б).

Для того, чтобы система находилась в положении устойчивого равновесия, ее потенциальная энергия должна быть минимальна.

D1H

а) q> 900

D1I

б) q< 900

Рис. 1.

Поэтому поверхность жидкости, налитой в сосуд, стремится сократиться до минимума (плоскость), и за счет изогнутой формы поверхности возникает дополнительное давление Dр, определяемое формулой Лапласа

, (3)

где R1 и R2 – радиусы кривизны двух взаимно перпендикулярных поверхностей. Знаки «+» и «–» указывают направление дополнительного давления.

D1J

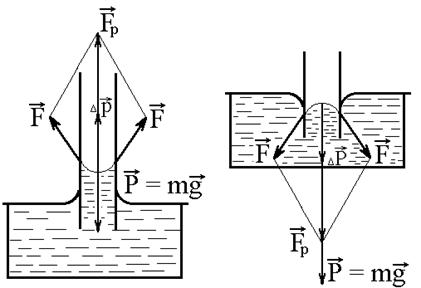
а) б)

Рис. 2.

Если жидкость налита в узкий цилиндрический сосуд малого диаметра (капиллярные трубки), то за счет дополнительного давления она поднимается вверх по трубке (в случае смачивающей жидкости) на высоту h, определяемую формулой Жюрена

, (4)

где θ – краевой угол смачивания; r – радиус капилляра; r - плотность жидкости. Капиллярные явления играют, большую роль в природе. Если поступление питательных веществ в корневую систему регулируется процессом диффузии, то подъем питательного раствора по стеблю или стволу растения в значительной мере обусловлен капиллярными явлениями: раствор поднимается по тонким капиллярным трубкам, образованным стенками растительных клеток.

У человека диаметр кровеносных капилляров в 10 раз тоньше человеческого волоса. Грунтовые воды поднимаются по капиллярам кирпичных стен домов. В некоторых механизмах смазка поступает к трущимся деталям через капилляры уплотнителей, воск поступает к месту горения по капиллярам фитиля.

Коэффициент поверхностного натяжения можно определить различными методами. В нашей работе он определяется методом отрыва кольца и методом счета капель.

Экспериментальная часть

1. Метод отрыва кольца

1. Проверьте состояние установки. Плоскость кольца должна быть

горизонтальна.

2. Отсчитайте положение указателя «а» на шкале ненагруженного динамометра, затем положение «b», когда на чашку положен груз массой m, выраженной в

кг. Вес определите по формуле Р = mg.

3. По формуле вычислите цену деления шкалы динамометра

(Н/дел).

4. Убрав грузик, поднимите кювету с водой при помощи кремальеры до

соприкосновения поверхности жидкости с кольцом. Опустите кювету, определите положение «с» указателя в момент отрыва кольца. Опыт повторите 3 раза и определите среднее значение сср.

5. По формуле Fср = k (cср - a) вычислите среднюю силу поверхностного

натяжения

6. По формуле l = π (d1 + d2) (где d1 и d2 – внешний и внутренний диаметры кольца) вычислите длину границы поверхностного слоя, ограниченного

кольцом.

7. По формуле вычислите коэффициент поверхностного натяжения воды.

8. Найдя по таблице значение коэффициента поверхностного натяжения воды при температуре опыта т найдите погрешности измерений.

9. Результаты измерений и вычислений занесите в таблицу 1.

Таблица 1

№ п/п

a

b

c

P, H

k,

H/дел

F,

H

l,

м

a,

Н/м

M±m

1

2

3

d2

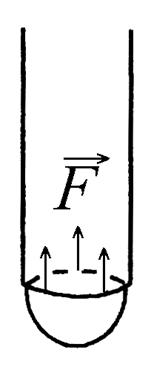
Рис. 3

2. Метод счета капель

Форма и размер капель, отрывающихся от конца капиллярной трубки, зависит не только от силы поверхностного натяжения, но и от диаметра трубки и плотности вытекающей жидкости (рис. 3). Перед отрывом капли образуется шейка, радиус r которой несколько меньше радиуса капиллярной трубки.

Вдоль окружности шейки действует сила поверхностного натяжения F = 2πrα, которая в момент отрыва равна силе тяжести капли Р = mg

2πrα = mg (5)

откуда (6)

Из-за сложности отсчета массы капли и радиуса шейки расчет по формуле (6) дает большие погрешности, поэтому используется метод сравнения коэффициента поверхностного натяжения исследуемой жидкости с коэффициентом поверхностного натяжения a0 эталонной жидкости (дистиллированной воды). Пусть из одинакового объема (между метками трубки) вытекает n капель исследуемой жидкости и n0 – капель эталонной жидкости. Массу одной капли жидкости выразим по формуле

, (7)

тогда выражение (5) для обеих жидкостей запишется:

; , (8)

где r и r0 – плотности исследуемой и эталонной жидкостей.

Считая радиусы шейки капли для обеих жидкостей мало отличающимися и преобразовав уравнение (8) относительно a, получим:

. (9)

1. В сталагмометр налейте дистиллированную воду и просчитайте количество капель n0 между метками, предварительно отрегулировав скорость их вытекания. Плотность r0 и коэффициент поверхностного натяжения a0 для температуры опыта выпишите из таблицы.

2. Промойте трубку 1% раствором исследуемой жидкости (поваренной соли), налейте такое же количество ее. Просчитайте количество капель между метками. По формуле (9) рассчитайте коэффициент поверхностного натяжения исследуемой жидкости.

3. Опыт повторите с 3, 7 и 9%-ми растворами этой жидкости и рассчитайте для них коэффициенты поверхностного натяжения. Плотность этих жидкостей указана на сосудах.

4. Занесите результаты в таблицу 2.

Таблица 2

Дистиллированная вода

Исследуемая

жидкость

1%

3%

7%

9%

Число капель

Плотность r, кг/м3

КПН a, Н/м

5. Вычертите график зависимости коэффициента поверхностного натяжения от концентрации раствора, откладывая по оси абсцисс концентрацию раствора, а по оси ординат значения коэффициента поверхностного натяжения.

6. Проделайте те же опыты для растворов сахара в воде.

7. Сделайте вывод, как меняется КПН в растворе сахара.

Вопросы к защите работы:

1. Дать определение КПН, указать единицы его измерения.

2. Какие силы называются молекулярными и как они изменяются при изменении расстояния между молекулами?

3. Что такое свободная энергия поверхности жидкости?

4. Какие вещества называются поверхностно активными?

5. Чем объясняется смачивание жидкостью поверхности твердого тела?

6. Какую форму имеет поверхность смачивающей и несмачивающей

жидкости?

7. Чем обусловлено и как направлено дополнительное давление? Как его рассчитать?

8. Как объяснить капиллярные явления? Как рассчитать высоту подъема жидкости в капиллярной трубке?

9. Выведите формулу коэффициента поверхностного натяжения методом счета

капель.

Лабораторная работа № 9

ОПРЕДЕЛЕНИЕ ДЛИНЫ СВОБОДНОГО ПРОБЕГА

И ЭФФЕКТИВНОГО ДИАМЕТРА МОЛЕКУЛЫ

Цель работы: экспериментальное определение эффективного диаметра и длины свободного пробега молекулы воздуха.

Оборудование: экспериментальная установка, секундомер.

Теоретическое введение

Согласно молекулярно-кинетической теории, хаотическое движение молекул является физической причиной наблюдаемых в газах явлений переноса (теплопроводность, диффузия, вязкость).

Хотя величины скоростей молекул относительно велики, но процессы переноса осуществляются сравнительно медленно.

Молекулярно-кинетическая теория позволила получить формулы, в которых макропараметры газа (давление, объем температура) связываются с его микропараметрами. Пользуясь этими формулами можно при помощи легко измеряемых макроскопических параметров получить интересующие нас микропараметры – размер молекулы и среднюю длину свободного пробега.

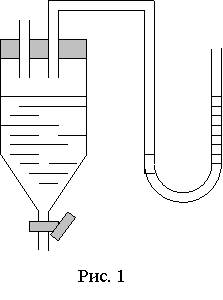Минимальное расстояние между центрами двух молекул, на котором происходит явление подобное удару, называется эффективным диаметром молекулы .

Расстояние, которое проходит молекула между двумя последовательными столкновениями, называется длиной свободного пробега молекулы .

В данной работе длина свободного пробега и эффективный диаметр молекулы воздуха определяются путем измерения коэффициента динамической вязкости воздуха.

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11