Количество теплоты, необходимое для нагревания газа на один градус, называется теплоемкостью газа. теплоемкости газов принято разделять на молярную и удельную:
а) молярная теплоемкость – величина, равная количеству теплоты, необходимому для нагревания 1 моля вещества на 1 Кельвин:
, (5)
где m – масса вещества, кг; m – молярная масса, кг/моль; DТ – разность температур, К. измеряется Дж/Моль×К.
б) удельная теплоемкость – величина, равная количеству теплоты, необходимому для нагревания единицы массы вещества на один Кельвин:
. (6)
измеряется в Дж/кг К.
Теплоемкость газа зависит от того, при каких условиях он нагревается: при постоянном объеме или при постоянном давлении. Если нагревать газ при постоянном объеме, то подводимая теплота идет только на увеличение его внутренней энергии. В этом случае говорят о теплоемкости при постоянном объеме или изохорной теплоемкости СV. Если нагревать газ при постоянном давлении, то подводимая теплота идет не только на увеличение внутренней энергии, но и на работу расширения. В этом случае говорят о теплоемкости при постоянном давлении или изобарной теплоемкости Ср.
Для идеального газа между изохорной и изобарной теплоемкостями по
закону Майера существует следующая связь
Cp = CV + R, (7)
где R = 8,314 Дж/Моль×К – универсальная газовая постоянная.
Тогда молярная теплоемкость при постоянном объеме может быть рассчитана из выражения
. (8)
Исходя из уравнения Майера,
. (9)
Адиабатическим называется процесс, протекающий без теплообмена с окружающей средой, т. е. dQ = 0. Первое начало термодинамики для адиабатического процесса запишется:
dU + dA = 0 или dA = –dU, или dU = –dA. (10)
Интегрирование этого уравнения приводит к уравнению Пуассона
, (11)
где g – показатель адиабаты (отношение молярной теплоемкости идеального газа при постоянном давлении к молярной теплоемкости при постоянном объеме):
. (12)
Через число степеней свободы показатель адиабаты выражается:
. (13)
При адиабатическом расширении газа (dA>0; dU<0) его температура понижается, а при сжатии (dA<0; dU>0) – повышается. Для осуществления этих процессов необходима абсолютная теплоизоляция системы от окружающей среды. На практике такие условия создать невозможно поэтому реальные процессы могут быть близки к адиабатическим, если теплообмен между системой и средой незначителен, или к изотермическим, если теплообмен хороший.
Адиабатическими можно считать процессы расширения и сжатия смеси в цилиндрах двигателей внутреннего сгорания. Особенно отчетливо это выражено в дизельных двигателях: адиабатическое сжатие смеси приводит к ее самовоспламенению. Адиабатическое расширение газа в морозильной камере холодильника сопровождается резким понижением температуры в ней. За счет механической работы, совершаемой компрессором, температура хладагента повышается и передается охладителю (воде или воздуху при комнатной температуре). По этому принципу работают тепловые насосы: теплота отбирается у низкопотенциальных источников (тепло грунта, океанской воды, молока на фермах и т. д.) и «перекачивается» в имеющую более высокую температуру окружающую среду. Подобный способ отопления оказывается более выгодным, чем непосредственное использование энергии, образующейся при сгорании топлива. Дополнительное преимущество тепловых насосов – возможность при соответствующем переключении понижать температуру в помещении в летний период.
Существуют различные методы определения показателя адиабаты. В данной работе для определения показателя адиабаты (адиабатической постоянной) воздуха используется метод интерференции звуковых волн и метод адиабатического расширения.
Экспериментальная часть
1. Метод интерференции звуковых волн
Одним из самых удобных и точных методов определения отношения 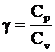 является метод, основанный на измерении скорости звука в газе. Скорость звука в газе, как известно из акустики, определяется по формуле
является метод, основанный на измерении скорости звука в газе. Скорость звука в газе, как известно из акустики, определяется по формуле
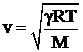 , (14)
, (14)
где: 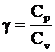 - отношение молярных теплоемкостей газа,
- отношение молярных теплоемкостей газа,
![]() - универсальная газовая постоянная,
- универсальная газовая постоянная,
![]() - молярная масса воздуха,
- молярная масса воздуха,
Т – абсолютная температура.
Из формулы (14) можно найти, что
![]() . (15)
. (15)
 |
Измерение скорости звука, в данной работе, основано на явлении интерференции звуковых волн.
Интерференцией называется явление наложения двух когерентных волн, приводящее к усилению волнового движения в одних точках и ослаблению или полному гашению в других. Когерентными называются волны, имеющие одинаковую частоту и постоянную во времени разность фаз.
Для получения когерентных звуковых волн поток энергии, излучаемый источником звука, разделяется на две части. Образующиеся при этом две звуковые волны направляют по путям различной длины, а затем снова соединяют. Амплитуда результирующей волны будет зависеть от разности фаз.
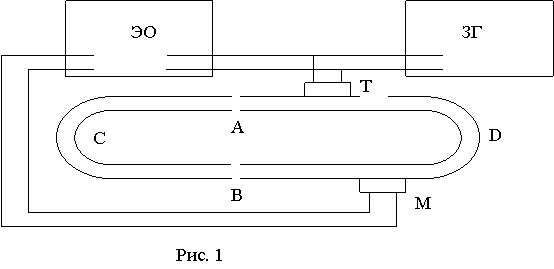
В лабораторной установке интерференция звуковых волн осуществляется с помощью двух труб ADB и ACB, вставленных друг в друга, причем колено ACB можно удлинять или укорачивать (рис. 1).
С помощью телефона Т в трубы излучается звук, частота которого задается звуковым генератором ЗГ. Когерентные звуковые волны проходящие по трубам ACB и ADB, сходятся у микрофона М. Возникающие в микрофоне переменные импульсы тока подают на вход «Y» электронного осциллографа ЭО. Развертка этих сигналов по горизонтали осуществляется от звукового генератора с той же частотой, что и частота колебаний мембраны телефона. На экране осциллографа электронный луч описывает траекторию, получающуюся при сложении двух взаимно перпендикулярных колебаний одинаковой частоты. Изменяя длину трубы ACB можно добиться того, чтобы у микрофона М был интерференционный максимум. При этом на экране осциллографа наблюдается прямая линия, наклоненная под углом ![]() к оси «Х».
к оси «Х».
Чтобы определить длину волны ![]() Нужно измерить то смещение трубы ACB, которое необходимо произвести для перехода от одного максимума к другому.
Нужно измерить то смещение трубы ACB, которое необходимо произвести для перехода от одного максимума к другому.
Известно, что максимум интерференции наблюдается в том случае, когда разность хода волн ![]() равна четному числу полуволн или целому числу длин волн, т. е.
равна четному числу полуволн или целому числу длин волн, т. е.
![]() , (15)
, (15)
где k = 0, 1, 2, 3,…….. .
Пусть для первого максимума
![]() , (16)
, (16)
тогда для следующего максимума можно написать
![]() . (17)
. (17)
Из (16) и (17) можно найти, что
![]() . (18)
. (18)
Для нашей установки смещение ![]() трубы ACB с величиной
трубы ACB с величиной 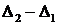 , очевидно, будет связано соотношением
, очевидно, будет связано соотношением
![]() . (19)
. (19)
С учетом (18) получим
![]() . (20)
. (20)
Известно, что
![]() . (21)
. (21)
Подставляя (19) в (20) окончательно получим
![]() . (22)
. (22)
Тогда для адиабатической постоянной воздуха можно получить
![]() . (23)
. (23)
Выделяя постоянную
![]() , (24)
, (24)
получим
![]() . (25)
. (25)
1. Включите звуковой генератор и осциллограф в сеть и дайте им
прогреться.
2. Установите частоту звука в пределах 1500 – 2500 Гц.
3. Выдвигая подвижную трубу ACB, добейтесь четкого изображения прямой, наклоненной под углом ![]() к горизонтали. Примите это положение трубы АСВ по измерительной шкале за начало отсчета измерения длины.
к горизонтали. Примите это положение трубы АСВ по измерительной шкале за начало отсчета измерения длины.
4. Продолжая выдвигать трубу, придите к исходной траектории луча и измерьте величину смещения трубы ![]() относительно указанного в п. № начала отсчета. Найдите среднее значение смещения трубы
относительно указанного в п. № начала отсчета. Найдите среднее значение смещения трубы ![]() .
.
5. Запишите значение абсолютной температуры и по формуле (24) вычислить значение константы k.
6. По формуле (25) найдите значение ![]() .
.
7. Опыт повторите не менее пяти раз на различных частотах.
8. Результаты измерений и расчетов занесите в таблицу 1.
9. Рассчитайте погрешность измерения.
Таблица 1
№№ | Т К |
|
м |
м |
м |
|
|
| δ, % |
1. | |||||||||
2. | |||||||||
3. | |||||||||
4. | |||||||||
5. |

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 |





