2. A = x ∙ y A = x/y ε = 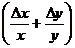∙ 100%

3. A = xn ε = n∙∙ 100%

4. A = en ε =∆x∙ 100%

5. A = sin x ε = |ctg x| . 100%

где: ∆ х и ∆ y - абсолютные ошибки отдельных величин.

Зная среднее значение величины A и относительную погрешность ε, можно найти значение абсолютной ошибки из определения:

ε = 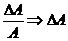= ε . A

Например, оценить абсолютную и относительную погрешность при определении плотно­сти цилиндра.

,

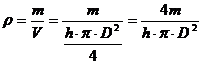где m - масса цилиндра, D - диаметр основания, h – высота.

ε =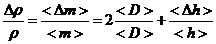

Абсолютную погрешность можно определить из соотношения:

ε =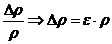

При определении абсолютных погрешностей отдельных измерений

(∆х, ∆у, ∆z) следует руководствоваться следующими правилами:

1. Если указатель измерительного прибора (стрелка, риска и т. д.) движется плавно, то абсолютная ошибка измерения равна половине цены деления шкалы.

2. Если указатель движется скачкообразно (например, механический секундомер), то абсолютная погрешность равна цене деления шкалы.

Точность измерительных приборов

Точностью измерительного прибора называется наименьшая величина, которую можно вполне надежно определять с помощью данного прибора.

Если точность прибора неизвестна, ее считают равной половине цены наименьшего деления шкалы прибора. Если измерения проводятся прибором, снабженным нониусом (штангенциркуль), то точность прибора принимается равной разности между ценой одного деления прибора и одного деления нониуса. Для электроизмерительных приборов погрешность измерения характеризуется классом точности в пределах от 0,05 до 4. Значение класса точности указывается на лицевой стороне прибора.

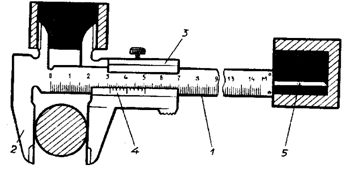
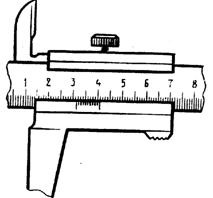
Штангенциркуль (рис.1,а, б) Состоит из подвижной и неподвижной измерительных губок 2, 3 и имеет две шкалы: (см. рис. 2,а): основная 1 и шкала 4 нониуса. Цена деления основной шкалы - 1мм, нониуса – 0,9 мм (см. рис. 2,б), таким образом, каждое деление нониуса короче деления штанги на 0,1 мм. точностью нониуса называется отношение цены деления шкалы основной линейки к числу делений нониуса. Чтобы измерить линейный размер предмета, его зажимают между измерительными губками штангенциркуля и делают отсчет по нониусу. Если нулевое деление нониуса совпадает с каким-нибудь делением шкалы (на штанге), то это деление указывает действительный размер в мм. Если нулевое деление нониуса не совпадает ни с одним делением основной шкалы,

а б

Рис. 1. Штангенциркуль: а) общий вид, б) нониус

то действительный размер равен сумме двух слагаемых: целому числу миллиметров, сложенному с дробной частью. Целое число миллиметров показывает ближайший штрих основной шкалы слева от нулевого штриха нониуса, а число десятых долей миллиметра равно порядковой цифре штриха нониуса, который точно совпал со штрихом основной шкалы (штанги).

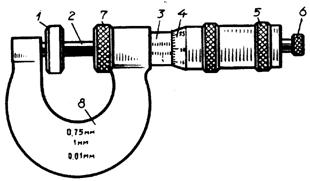
Микрометр (рис. 2, а, б) представляет собой массивную металлическую скобу 8, с одной стороны которой имеется неподвижная измерительная пятка, с другой – стебель 2, снаружи охватываемый барабаном 4, соединенный с микрометрическим винтом 7. На правом конце стебля микрометра имеется трещотка, предназначенная дляобеспечения постоянства измерительного усилия. На поверхность стебля микрометра нанесена продольная риска, вдоль которой (выше и ниже ее) нанесены миллиметровые штрихи 3.

а б

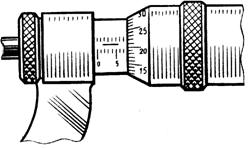
Рис. 2 Микрометр: а) общий вид, б) шкала барабана

Верхние штрихи делят нижние пополам. Эта шкала называется основной. Вторая шкала нанесена на окружность скоса барабана и называется круговой шкалой 4. Цена деления основной шкалы – 1мм, круговой шкалы -0,01 мм.

Показания микрометра складываются из показаний основной шкалы и шкалы барабана (см. рис. 3 б). Порядковый номер видимого нижнего штриха основной шкалы перед кромкой барабана равен целому числу миллиметров. Если перед кромкой барабана виден еще и штрих сверху, то к числу миллиметров нужно прибавить еще 0,5 мм. Число сотых долей миллиметра равно порядковому номеру штриха на шкале барабана, совпадающего с продольным штрихом шкалы.

Лабораторная работа № 1

МАТЕМАТИЧЕСКИЙ МАЯТНИК

Цель работы: изучение свободных колебаний маятника,

определение ускорения свободного падения.

Оборудование: лабораторная установка, секундомер.

Теоретическое введение

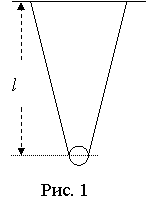
Математическим маятником называется тело, подвешенное на длинной невесомой нити, длина которой во много раз превышает линейные размеры тела (рис. 1).

Период колебаний математического маятника определяется по приближенной формуле, при­годной только для малых амплитуд колебаний:

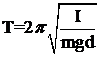, (1)

где I - момент инерции маятника относительно оси колебаний,

m - масса маятника,

d - расстояние от оси до центра масс маятника, в данном случае равное длине нити маятника l

g - ускорение свободного падения.

Математический маятник представляет собой механическую колебательную систему, колебания в которой происходят под действием квазиупругой силы:

,

где k – коэффициент жесткости колебательной системы,

х – смещение системы от положения равновесия.

Система, движущаяся под действием квазиупругой силы, называется одномерным гармоническим осциллятором.

Уравнение второго закона Ньютона для одномерного гармонического осциллятора можно записать в виде

. (2)

Так как а= x″, то уравнение (2) можно преобразовать к виду

mx″ + kx = 0 (3)

Разделив все члены уравнения на m, и с учётом того, что -

собственная частота колебаний системы, получим уравнение движения одномерного гармонического осциллятора:

. (4)

Его решение имеет вид:

x = A cos (ω0t +φ0 ), (5)

где A – амплитуда колебаний, φ0 – начальная фаза колебаний

В настоящей работе проводится проверка соотношения (1) в случае, когда ма­ятник можно приближенно считать математическим, т. к. масса маятника сосредото­чена в области, размеры которой малы по сравнению с длиной маятника.

Исследуемый в данной работе маятник представляет собой стальной шарик радиусом R на бифилярном подвесе, тонкая нить проходит через центр масс шарика. Длина подвеса может регулироваться, период колебаний маятни­ка с высокой точностью измеряется электронным секундомером (рис. 1).

Пренебрегая моментом инерции нити, ввиду его ма­лости, запишем момент инерции маятника по теореме Штейнера в виде:

I=Ic + ml 2 = mR 2 + ml 2

В первом приближении, с учетом того, что l >> R можно получить

I =m l 2 (7)

С учетом (7) период колебания маятника можно записать в виде:

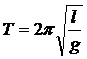
. (8)

Из (8) можно найти выражение для ускорения свободного падения

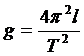(9)

Экспериментальная часть

Соотношение (9) позволяет опытным путем определить ускорение свободного падения. Для этого необходимо измерить период колебания маятника Т и длину подвеса l.

Но прежде необходимо выяснить, применимо ли соотношение (9) для лабо­раторной установки. Так как соотношение (1) справедливо для идеализированной модели физического маятника, то и соотношение (9) справедливо только в рамках этой модели.

При выводе соотношения (1) были сделаны следующие предположения:

- маятник совершает колебания с малой амплитудой;

- затуханием колебаний можно пренебречь.

1. Определите период колебания маятника при различных значениях амплитуды в пределах до , для чего измерьте время t, в течение, которого маятник совершает N колебаний и по формуле 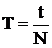рассчитайте период колебания. Результаты измерений занесите в таблицу 1.

Таблица 1

2. Проверьте, подтверждается ли на опыте линейная зависимость между квадратом периода колебаний и длиной маятника. Для этого измерьте период колебания маятника для четырех – пяти длин подвеса в пределах от lmin до lmax..0 При измерениях амплитуда колебаний должна быть малой. Результаты измерений занесите в таблицу 2

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11