4.  Что называется физическим маятником?

5.  От чего зависит период колебаний физического маятника?

6.  Что называется приведенной длиной физического маятника?

7.  Приведите вывод рабочей формулы.

Лабораторная работа № 3

ПРОВЕРКА ОСНОВНОГО УРАВНЕНИЯ ДИНАМИКИ

ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

Цель работы: экспериментальная проверка основного уравнения

динамики вращательного движения и определение момента

инерции диска.

Оборудование: экспериментальная установка, секундомер.

Теоретическое введение

Движение тела, вращающегося вокруг неподвижной оси, описывается основным уравнением динамики вращательного движения

, (1)

где: I – момент инерции тела относительно той же оси,

- угловое ускорение,

M – суммарный момент сил, действующих на тело.

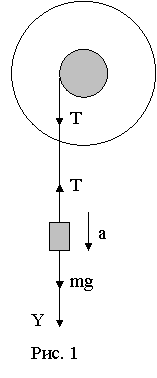Экспериментальная установка представляет собой диск массой и радиусом R и жестко скрепленный с ним шкив массой и радиусом r, способный вращаться вокруг горизонтальной оси. На шкив намотана нить, к свободному концу которой подвешивается груз массой m (рис. 1). Падающий груз приводит во вращение и диск со шкивом. При этом движение и груза и диска будут близки к равноускоренному.

Запишем второй закон Ньютона для груза и диска. Груз m движется поступательно и его уравнение движения в проекции на ось Y, будет иметь вид:

, (2)

где Т – сила натяжения нити,

а – ускорение груза.

Диск и шкив вращаются как единое целое. Уравнение движения этой системы будет иметь вид

, (3)

где I – момент инерции системы,

М – вращающий момент силы натяжения нити,

- вращающий момент сил трения.

Точка касания шнура и шкива является общей, и их движение при отсутствии проскальзывания характеризуется одним и тем же линейным ускорением а, связанным с угловым ускорением соотношением

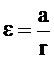. (4)

Вращающий момент силы натяжения нити

. (5)

Из уравнения (2) найдем силу натяжения нити

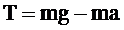. (6)

Так как a = ε∙r, то умножив обе части уравнения (6) на r, получим:

T = mgr –mεr2 (7)

Подставив правую часть уравнения (7) в уравнение (3), получим:

. (8)

После преобразований можно получить

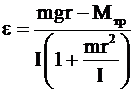. (9)

Для лабораторной установки выполняется условие

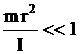. (10)

Учитывая это условие, окончательно получим

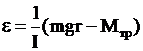, (11)

где момент внешней силы mg.

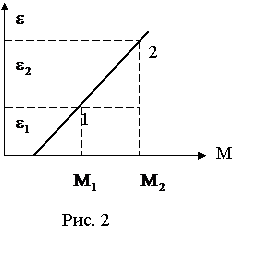
Если по горизонтальной оси откладывать момент внешней силы М, а по вертикальной оси – угловое ускорение , то график этой зависимости представляет собой прямую линию, не проходящую через начало координат и отсекающую на оси моментов отрезок равный (рис. 2). Угловой коэффициент этой прямой, как это легко получить, составит:

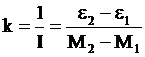. (12)

Отсюда

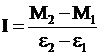. (13)

Целью данной работы является проверка уравнения (11), определение момента сил трения и момента инерции диска.

Оценить момент сил трения можно следующим образом. Если под действием груза массой система не движется, а груз массой приводит ее в равноускоренное движение, то, очевидно, что момент сил трения будет удовлетворять условию

. (14)

Экспериментальная часть

1. Используя данные лабораторной установки, по формуле

рассчитайте теоретическое значение момента инерции

системы.

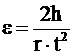2. Подвесьте к нити груз массой 100 г и определите время t падения груза с высоты h. Опыт проделайте не менее трех раз и найдите среднее значение времени падения. По формуле найдите угловое ускорение диска.

3. По формуле рассчитайте момент внешней силы.

4. Опыт повторите с грузами массой 200 и 300 г.

5. Результаты измерений и расчетов занесите в таблицу 1.

Таблица 1

№

кг

кг

R м

r м

m кг

h м

t с

M

I

1.

2.

3.

6. Постройте график зависимости 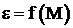и по графику определить момент сил трения

7. Используя график по формуле (13), найдите среднее значение момента инерции I системы. Рассчитайте погрешность измерения.

8. Оцените момент сил трения на опыте и проверьте, удовлетворяет ли найденное значение условию (14).

Вопросы к защите работы:

1.  Приведите вывод рабочей формулы.

2.  Запишите основное уравнение динамики вращательного движения.

3.  Физический смысл момента инерции твердого тела.

4.  Что называется моментом силы относительно точки и оси?

5.  Что называется угловым ускорением?

Лабораторная работа № 4

ОПРЕДЕЛЕНИЕ АДИАБАТИЧЕСКОЙ ПОСТОЯННОЙ

ВОЗДУХА

Цель работы: экспериментальное определение отношения .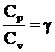

Оборудование: экспериментальная установка, звуковой генератор,

электронный осциллограф.

Теоретическое введение

Рассмотрим термодинамическую систему, для которой механическая энергия не изменяется, а изменяется лишь ее внутренняя энергия. Внутренняя энергия системы может изменяться в результате различных процессов, например совершения над системой работы или сообщения ей теплоты. При этих превращениях соблюдается закон сохранения и превращения энергии; применительно к термодинамическим процессам этим законом является первое начало термодинамики, установленное в результате обобщения многовековых опытных данных. Оно может быть сформулировано следующим образом: энергия в форме теплоты, сообщенная телу, идет на изменение его внутренней энергии и на работу расширения, которую выполняет газ против внешних сил

dQ = dU + dA, (1)

где dU – изменение внутренней энергии; dA – работа расширения; dQ – энергия в форме теплоты.

Внутренняя энергия – это кинетическая энергия движения частиц и потенциальная энергия их взаимодействия. Для идеального газа потенциальной энергией взаимодействия пренебрегают и рассматривают внутреннюю энергию как кинетическую энергию движения частиц. Энергия одной молекулы газа определяется формулой

, (2)

где i – число степеней свободы – число независимых координат, определяющих положение молекулы в пространстве, k – постоянная Больцмана, Т – абсолютная температура.

Энергия одного моля газа, содержащего число молекул, равное числу Авогадро NA, рассчитывается по формуле:

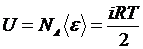. (3)

Работа расширения газа связана с изменением его объема. Ее можно рассчитать по формуле:

. (4)

Интегрирование выражения производится для конкретного процесса.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11