Из (2) можно найти 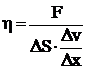. (3)

Очевидно, что при 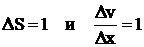, . Коэффициент динамической вязкости численно равен силе внутреннего трения, действующей на единичную площадку соприкасающихся слоев, при градиенте скорости между ними равном единице.

Одним из наиболее простых методов определения коэффициента динамической вязкости жидкости является метод Стокса, основанный на изучении движения тела сферической формы (шарика) в вязкой среде (рис. 2).

На шарик, свободно движущийся в такой среде, действуют:

Сила тяжести , (4)

где - плотность материала шарика,

R – его радиус.

Сила Архимеда 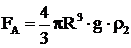, (5)

где - плотность жидкости.

Сила сопротивления (сила внутреннего трения). Как показал Стокс, при малых скоростях движения v, сила сопротивления может быть определена по формуле

, (6)

где - коэффициент динамической вязкости жидкости.

Следует подчеркнуть, что здесь играет роль не трение шарика о жидкость, а трение отдельных слоев жидкости друг о друга, так как при соприкосновении твердого тела с жидкостью к поверхности тела тот час же прилипают молекулы жидкости. Тело обволакивается слоем жидкости, который движется вместе с ним.

Равнодействующая этих сил

. (7)

Проекция N на вертикальное направление равна

. (8)

Вначале шарик будет двигаться равноускоренно, так как

. (9)

(т. е. ).

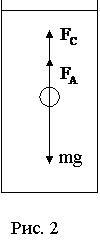С увеличением скорости шарика растет и сила сопротивления и наступает момент, когда равнодействующая N становится равной нулю. Это соответствует условию

. (10)

Начиная с этого момента шарик, движется равномерно с достигнутой скоростью v. Такое движение называется установившимся. При этих условиях начинает действовать закон Стокса. Для определения скорости дают шарику пройти равномерно некоторый путь h, в течение некоторого время t. Тогда

. (11)

Подставляя в (10) выражения (4), (5), (6), получим

. (12)

Подставляя выражение (11) в уравнение (12), получим выражение для определения коэффициента динамической вязкости:

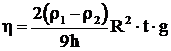. (13)

Введя обозначение

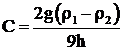, (14)

окончательно получим . (15)

Полученное выражение справедливо для случая, когда шарик падает в жидкости, простирающейся безгранично по всем направлениям, что невозможно осуществить на опыте, так как жидкость всегда находится в каком-то сосуде. Для уменьшения погрешности надо стремиться к тому, чтобы шарик падал вблизи середины столба жидкости в широком сосуде радиуса r >> R.

Экспериментальная часть

1. Записав значения и h, найдите значение константы С.

Плотность свинца - ρ1 =11300 кг/м3;

плотность касторового масла - ρ1 =960 кг/м3

2. Микрометром измерьте диаметр шарика и вычислите его радиус R.

3. Опустив шарик в сосуд с жидкостью, определите время t, в течение которого шарик проходит расстояние h на участке равномерного движения.

4. Опыт повторите не менее пяти раз и определите среднее значение коэффициента динамической вязкости касторового масла.

5. Результаты измерений и расчетов занести в таблицу 1.

Таблица 1

1.  Зная температуру жидкости можно найти табличное значение коэффициента динамической вязкости масла .

2.  Определите погрешность измерения .

Зависимость коэффициента динамической вязкости от температуры

Вопросы к защите работы:

1.  Запишите формулу Ньютона для силы внутреннего трения.

2.  Каков физический смысл коэффициента динамической вязкости?

3.  Что называется градиентом скорости?

4.  Запишите выражение для силы Стокса.

5.  Приведите вывод рабочей формулы.

Лабораторная работа № 8

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА

ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ ЖИДКОСТЕЙ

Цель работы: определение коэффициента поверхностного натяжения

жидкостей.

Оборудование: чашка с водой, алюминиевые кольца, пружина, линейка,

капельница, весы.

Теоретическое введение

На молекулы жидкости, расположенные на ее поверхности со стороны других молекул действуют силы, направленные внутрь жидкости, вследствие чего поверхностный слой жидкости производит на остальные слои молекулярное давление, в результате которого жидкость принимает такую форму, чтобы поверхность ее была наименьшей при данном объёме (роса в форме шарика).

Напряженное состояние поверхностного слоя жидкости называется поверхностным натяжением и вызвано силами притяжения между молекулами этого слоя.

Сумма сил притяжения, действующих на контур, ограничивающий поверхность жидкости, называется силой поверхностного натяжения. Отношение силы поверхностного натяжения, действующей на контур, ограничивающий поверхность жидкости, к длине этого контура называется коэффициентом поверхностного натяжения:

. (1)

Измеряется коэффициент поверхностного натяжения в Н/м.

При растяжении поверхности жидкости из ее глубины к поверхности перемещаются молекулы, при этом совершается работа против сил молекулярного притяжения и потенциальная энергия поверхности жидкости увеличивается. При уменьшении поверхности молекулярные силы совершают работу по перемещению молекул внутрь и потенциальная энергия поверхности уменьшается. Эта энергия называется свободной энергией поверхности жидкости W.

Коэффициент поверхностного натяжения (КПН) может быть определен как отношение свободной энергии поверхности жидкости к площади этой поверхности.

, (2)

измеряется КПН в =

Величина КПН изменяется в зависимости от находящихся в жидкости примесей. Вещества, ослабляющие поверхностное натяжение, называются

поверхностно активными веществами – ПАВ (нефть, спирт, эфир, мыло). Соль и сахар увеличивают силу поверхностного натяжения. На действии ПАВ основан метод борьбы с малярийными комарами, личинки которых тонут, если поверхность зараженного водоема полита нефтью, ослабляющей поверхностное натяжение.

Листья и стебли растений покрыты тонким воскообразным налетом –

кутикулой, не смачивающейся водой, поэтому не размокают под дождем деревья, стога сена, скирды соломы.

Молекулы жидкости взаимодействуют не только друг с другом, но и с молекулами твердых тел. Если взаимодействие между молекулами самой жидкости больше взаимодействия между молекулами жидкости и твердого тела, то такая жидкость будет несмачивающей (рис. 1, а). Если же силы взаимодействия между молекулами жидкости и твердого тела больше сил взаимодействия между молекулами самой жидкости, то жидкость будет смачивающей

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11