. (7)

Экспериментальная часть

1. Запишите из данных лаборатории длину и диаметр испытываемой

проволоки.

2. Вращая наружное кольцо индикатора, установите стрелку на нулевое деление шкалы.

3. На подвес положите груз массой m и определите абсолютное удлинение проволоки под действием этого груза.

4. По формулам (2) и (7) рассчитайте .

Опыт повторите не менее 4 – 5 раз с грузами различной массы.

5. Результаты измерений и расчетов занесите в таблицу 1.

Таблица 1

6. По полученным данным постройте график зависимости 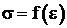и сравните его с теоретической зависимостью. По графику найдите модуль Юнга и определите погрешность измерения .

Вопросы к защите работы:

1.  Что называется деформацией тела? Какая деформация называется упругой? Остаточной?

2.  Что называется абсолютной и относительной деформацией?

3.  Сформулируйте закон Гука. Физический смысл модуля Юнга.

4.  Дайте анализ диаграммы полученной при испытании образца на статическое растяжение.

Лабораторная работа № 6

ОПРЕДЕЛЕНИЕ ИЗМЕНЕНИЯ ЭНТРОПИИ

В РЕАЛЬНЫХ СИСТЕМАХ

Цель работы: расчет изменения энтропии замкнутой системы.

Оборудование: нагреватель, калориметр, термометр, набор тел.

Теоретическое введение.

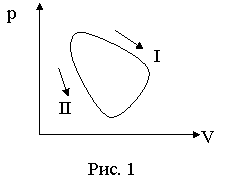Круговым процессом (циклом) называется процесс, при котором система, пройдя ряд состояний, возвращается в исходное состояние. На pV – диаграмме цикл изображается замкнутой кривой (рис. 1). Если цикл осуществляется по часовой стрелке (I), то он называется прямым, если в противоположном направлении – обратным. Первый осуществляется в тепловых двигателях, второй - в холодильных машинах.

Цикл называется обратимым, если он может осуществляться как в прямом, так и в обратном направлении и при этом в окружающей среде и в самой системе не происходит никаких изменений.

Величина получила название приведенного количества теплоты.

Теоретический анализ показывает, что для любого обратимого цикла сумма приведенных количеств теплоты равна нулю, т. е.

. (1)

Из равенства нулю этого интеграла следует, что подынтегральная функция является полным дифференциалом некоторой функции S, которая является функцией состояния системы, т. е.

. (2)

Эта функция получила название энтропии системы S.

Энтропия обладает тем свойством, что 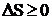(неравенство Клаузиуса), т. е. энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов).

Таким образом, для того чтобы ответить на вопрос, возможен ли в изолированной системе тот или иной процесс, необходимо рассчитать происходящее в этом процессе приращение энтропии. Если оно оказывается положительным, то рассматриваемый процесс возможен, так как в результате его энтропия системы возрастает. Те же процессы, при которых приращение энтропии оказывается отрицательным, в изолированной системе невозможны, поскольку в этом случае энтропия изолированной системы должна уменьшаться. В незамкнутой системе энтропия может как увеличиваться, так и уменьшаться.

Учитывая (2) для конечного приращения энтропии можно получить:

. (3)

Так как при нагревании тела , то

, (4)

где - конечная температура тела, - начальная температура тела.

В силу аддитивности энтропии, для системы тел можно получить:

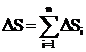. (5)

Лабораторная установка состоит из калориметра, массой и теплоемкостью , в котором находится вода массой и теплоемкостью при температуре . Если в калориметр опустить тело массой и теплоемкостью , предварительно нагретое до температуры , то в результате теплообмена в калориметре установится конечная температура .

По формуле (4) найдем изменение энтропии каждого тела в процессе теплообмена.

Для калориметра: 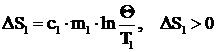, (6)

для воды: 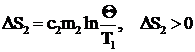, (7)

для тела: 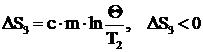. (8)

Экспериментальная часть

1. Включите нагреватель, предварительно поместив в него испытуемые

тела.

2. Налейте в калориметр некоторое количество (150 – 200 г.) воды и измерьте начальную температуру воды и калориметра.

3. После того как закипит вода в нагревателе, испытуемое тело быстро перенесите в калориметр и закройте его крышкой. Измерить конечную температуру , установившуюся в калориметре.

4. По формулам (6), (7) и (8) рассчитайте изменение энтропии каждого тела.

5. По формуле (5) рассчитайте изменение энтропии системы и сделайте вывод.

6. Опыт повторите с другими телами.

Вопросы к защите работы:

1.  Как читаются первое и второе начала термодинамики?

2.  Что такое энтропия?

3.  Какие процессы называются обратимыми? необратимыми?

4.  Запишите неравенство Клаузиуса. В чем его смысл?

5.  В чем заключается статистический смысл второго начала

термодинамики?

Лабораторная работа № 7

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА

ДИНАМИЧЕСКОЙ ВЯЗКОСТИ ЖИДКОСТЕЙ

Цель работы: экспериментальное определение коэффициента

динамической вязкости жидкостей.

Оборудование: сосуды с касторовым маслом и глицерином, шарики,

микрометр, секундомер.

Теоретическое введение

Вязкостью или внутренним трением называется способность частиц жидкости сопротивляться относительному перемещению (сдвигу).

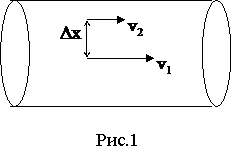Если наблюдать медленное движение жидкости в прозрачной трубе, то легко убедиться в том, что жидкость перемещается отдельными слоями, которые движутся с различными скоростями (рис. 1). У оси трубы скорость максимальна, у стенок трубы она равна нулю. Слои жидкости скользят относительно друг друга. Величина, характеризующая изменение скорости от слоя к слою называется градиентом скорости. Это векторная величина, направленная перпендикулярно скорости и численно равная отношению

, (1)

где - расстояние между слоями.

Со стороны частиц, движущихся более быстро, действуют силы, ускоряющие частицы, движущиеся медленнее и наоборот, слои находящиеся у стенок стремятся затормозить более быстрые слои жидкости.

Эти силы носят название сил внутреннего трения или вязкости. Силы внутреннего трения всегда направлены по касательной к поверхности слоев, движущихся с различными скоростями, и определяются по формуле Ньютона

, (2)

где: - площадь поверхности соприкасающихся слоев,

- коэффициент динамической вязкости, зависящий от рода жидкости и ее температуры.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11