Лабораторный практикум по механике и молекулярной физике (стр. 11 )

.

При записи скалярного произведения символы перемножаемых векторов пишутся рядом без какого-либо знака между ними. Скалярное произведение двух взаимно перпендикулярных векторов равно нулю. Под квадратом вектора понимается скалярное произведение вектора на самого себя . Таким образом, квадрат вектора равен квадрату его модуля .

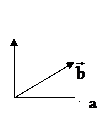
Векторное произведение векторов

Векторным произведением векторов называется вектор , модуль которого определяется выражением

,

а направление – правилом правого винта. Направление вектора совпадает с направлением поступательного перемещения правого винта, если его поворачивать от первого вектора ко второму по кратчайшему пути. Символически векторное произведение записывается двумя способами

.

Векторы, направления которых связывается с направлением вращения, называются псевдовекторами или осевыми векторами.

Поскольку направление векторного произведения определяется направлением вращения от первого сомножителя ко второму, то результат векторного умножения зависит от порядка сомножителей. Перестановка сомножителей вызывает изменение направления результирующего вектора на противоположное, т. е.

.

ПРИЛОЖЕНИЕ 2

Некоторые формулы тригонометрии

, , ,

, ,

,

,

,

,

.

ПРИЛОЖЕНИЕ 3

Формулы дифференцирования

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

ПРИЛОЖЕНИЕ 4

Таблица интегралов

, , ,

, ,

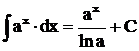ПРИЛОЖЕНИЕ 5

О системе единиц и размерности физических величин

Законы физики устанавливают количественные отношения между физическими величинами. Для установления таких соотношений необходимо иметь возможность измерять физические величины.

Измерить какую-либо физическую величину означает сравнить ее с однородной величиной, условно принимаемой за единицу.

Вообще говоря, единицы измерения каждой физической величины можно было бы выбирать произвольно, но это приводит к усложнению формул отражающих количественные соотношения между величинами. Гаусс показал, что можно ограничиться произвольным выбором единиц измерения нескольких (не менее трех) в принципе любых величин, принятых за основные. Единицы же всех остальных величин можно устанавливать с помощью основных, воспользовавшись для этого физическими законами, связывающими эти величины.

При указанном способе выбора единиц измерения физических величин количественные соотношения принимают наиболее простой вид. Совокупность всех единиц измерения образует систему единиц. Системы единиц, построенные по данному способу, получили название самосогласованных.

Существует несколько систем, отличающихся выбором основных единиц. Системы, в основу которых положены единицы длины, массы и времени получили название абсолютных.

В России с 1 января 1963 года принята Международная система единиц (СИ).

Основными единицами СИ являются:

- единица длины - метр (м) – длина 1650763,73 длин волн в вакууме излучения, соответствующего переходу между уровнями и атома криптона 86;

- единица времени - секунда (с) - промежуток времени равный сумме 9192631770 периодов излучения, соответствующих переходу между двумя сверхтонкими уровнями основного состояния атома цезия 133;

- единица массы - килограмм (кг) - масса платино-иридиевого цилиндра диаметром и высотой 39 мм.

Из способа построения системы единиц следует, что изменение основных единиц влечет за собой изменение производных величин.

Соотношение, показывающее, как изменяется единица какой-либо величины при изменении основной единицы, называется размерностью данной величины.

Поскольку физические законы не могут зависить от выбора единиц измерения фигурирующих в них величин, то размерности обеих частей должны быть одинаковы.

Для размерности основных величин используются специальные обозначения: длина , время , масса .

В указанных обозначениях размерность произвольной физической величины будет иметь вид (при этом могут быть как положительными, так и отрицательными и, в частности, могут быть равными нулю).

Например, размерность скорости , а силы .

ПРИЛОЖЕНИЕ 6

Плотность вещества, кг/м3

ПРИЛОЖЕНИЕ 7

МОДУЛЬ УПРУГОСТИ (ЮНГА)

ПРИЛОЖЕНИЕ 8

Динамическая вязкость некоторых веществ*, мкПа × с

* В скобках указана температура, при которой приводится данное значение вязкости

ПРИЛОЖЕНИЕ 9

ТАБЛИЦА ЗАВИСИМОСТИ ОТ ТЕМПЕРАТУРЫ, ПЛОТНОСТИ, ВЯЗКОСТИ И

ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ ВОДЫ, СПИРТА И КАСТОРОВОГО МАСЛА

ЛИТЕРАТУРА

1.  Савельев общей физики, т. 2. М.: Наука.- 2008 .

2.  Трофимова физики. М.: Высшая школа.- 2010.

3.  Волькенштейн B. C. Сборник задач по общему курсу физики. М.: Наука.-1999.

4.  Трофимова задач по курсу физики. М.: Высшая школа.- 2002.

5.  , Воробьев по физике. М.: Высшая школа.-2001 .

6. , Власенко для самостоятельной работы по

физике студентов технических специальностей. Ставрополь, Агрус.-2004

7. Крахоткин и молекулярная физика. Ставрополь, Агрус.- 2006

СОДЕРЖАНИЕ

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11