![]() - формула 5
- формула 5
Соблюдая это условие, можно получать эквивалентные результаты, начисляя проценты как по формуле (3), так и по формуле (4). Антисипативным методом начисления процентов обычно пользуются в чисто технических целях, в частности, для определения суммы, дисконтирование которой по заданным учетной ставке и сроку, даст искомый результат. В следующем параграфе будут рассмотрены конкретные примеры возникновения подобных ситуаций.
Как правило, процентные ставки устанавливаются в годовом исчислении, поэтому они называются годовыми. Особенностью простых процентов является то, что частота процессов наращения в течение года не влияет на результат. То есть, нет никакой разницы начислять 30% годовых 1 раз в год или начислить 2 раза по 15% годовых. Простая ставка 30% годовых при одном начислении в году называется эквивалентной простой ставке 15% годовых при начислении 1 раз в полгода. Данное свойство объясняется тем, что процесс наращения по простой процентной ставке представляет собой арифметическую прогрессию с первым членом a1 = P и разностью d = (P*i).
P, P + (P*i), P + 2*(P*i), P + 3*(P*i), …, P+(k–1)*(P*i)
Наращенная сумма S есть ничто иное, как последний k-й член этой прогрессии (S = ak = P + n*P*i), срок ссуды n равен k – 1. Поэтому, если увеличить n и одновременно пропорционально уменьшить i, то величина каждого члена прогрессии, в том числе и последнего, останется неизменной.
Однако продолжительность ссуды (или другой финансовой операции, связанной с начислением процентов) n необязательно должна равняться году или целому числу лет. Напротив, простые проценты чаще всего используются при краткосрочных (длительностью менее года) операциях. В этом случае возникает проблема определения длительности ссуды и продолжительности года в днях. Если обозначить продолжительность года в днях буквой K (этот показатель называется временная база), а количество дней пользования ссудой t, то использованное в формулах (3) и (4) обозначение количества полных лет n можно будет выразить как t/K. Подставив это выражение в (3) и (4), получим:
для декурсивных процентов: ![]() - формула 6
- формула 6
для антисипативных процентов: ![]() - формула 7
- формула 7
Способы подсчета временной базы
В различных случаях могут применяться различные способы подсчета числа дней в году (соглашение по подсчету дней). Год может приниматься равным 365 или 360 дням (12 полных месяцев по 30 дней в каждом). Проблема усугубляется наличием високосных лет. Например, обозначение ACT/360 (actual over 360) указывает на то, что длительность года принимается равной 360 дням. Однако возникает вопрос, а как при этом определяется продолжительность ссуды?
Например, если кредит выдается 10 марта со сроком возврата 17 июня этого же года, как считать его длительность – по календарю или исходя из предположения, что любой месяц равен 30 дням? Безусловно, в каждом конкретном случае может быть выбран свой оригинальный способ подсчета числа дней, однако на практике выработаны некоторые общие принципы, знание которых может помочь сориентироваться в любой конкретной ситуации.
Если временная база (K) принимается равной 365 (366) дням, то проценты называются точными. Если временная база равна 360 дням, то говорят о коммерческих или обыкновенных процентах. В свою очередь подсчет длительности ссуды может быть или приближенным, когда исходят из продолжительности года в 360 дней, или точным – по календарю или по специальной таблице номеров дней в году. Определяя приближенную продолжительность ссуды, сначала подсчитывают число полных месяцев и умножают его на 30. Затем добавляют число дней в неполных месяцах. Общим для всех способов подсчета является правило: день выдачи и день возврата кредита считаются за 1 день (назовем его граничный день).
В приведенном выше условном примере точная длительность ссуды составит по календарю 99 дней (21 день в марте + 30 дней в апреле + 31 день в мае + 16 дней в июне + 1 граничный день). Тот же результат будет получен, если использовать таблицу номеров дней в году (10 марта имеет порядковый номер 69, а 17 июня – 168). Если же использовать приближенный способ подсчета, то длительность ссуды составит 98 дней (21 + 2*30 + 16 + 1).
Наиболее часто встречаются следующие комбинации временной базы и длительности ссуды (цифры в скобках обозначают соответственно величину t и K):
Точные проценты с точным числом дней (365/365).
Обыкновенные (коммерческие) проценты с точной длительностью ссуды (365/360).
Обыкновенные (коммерческие) проценты с приближенной длительностью ссуды (360/360).
Понятие аннуитета
Аннуитет (annuity) — несколько равновеликих выплат в течение определенного числа лет.
Аннуитет можно охарактеризовать как несколько равновеликих выплат из первоначальной суммы, производящихся в течение ряда лет. На Рис. 3 показаны потоки денежной наличности для аннуитета. В течение определенного срока, в данном случае 5 лет, из исходной суммы делаются фиксированные выплаты. Суммарные отчисления превышают сумму депозита из-за использования сложных процентов.
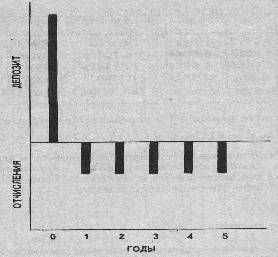
Рис. 3. Потоки денежной наличности при аннуитете
Предположим, вам достались по наследству 10 000 долларов, и вы хотите иметь стабильный в течение ближайших 10 лет доход. Некая страховая компания предлагает такие аннуитеты из расчета 5% годовых. Какова же сумма ежегодного дохода?
По формуле конечной (будущей) стоимости через 10 лет данная сумма будет равна 0, поскольку вся сумма должна быть выплачена. Мы также знаем, что X0 = $10 000, г = 0,05; n = 10. Отсюда нам нужно найти х, которое, как мы знаем, будет отрицательным, ибо это выплаты.
Значит,
0 = (10 000 - х/0,05)(1,05)10 + х/0,05 = (10 000 – 20х) (1,628894) + 20х;
32,57788x = 20х – 16 288,94;
12,57788x = 16 288,94;
х = $1 295,05.
Таким образом, приобретя аннуитет, вы в течение 10 лет можете получать ежегодно по 1295,05 дол.
Возвращаясь к нашим примерам, мы также можем определить размер суммы, которую нужно положить на счет в банке, чтобы обеспечить вкладчику определенные поступления в течение ряда лет. Если банк выплачивает 8% годовых, какова должна быть величина первоначальной суммы?
В данном случае, где х равно 5 000 долларов, через 10 лет конечная стоимость будет равна 0, (Fn = 0). При r = 0,08, уравнение имеет вид:
0 = (Xо – 5 000/0,08) (1,08)10 + 5 000/0,08.
Находим X0,
0 = (X0 - 62 500)(2,1589) + 62 500;
2,1589 X0 = 72 431;
X0 = $33 550.
Следовательно, чтобы получать по 5000 долларов ежегодно в течение ближайших 10 лет, нужно положить на счет 33 500 долларов.
Эмпирические правила удвоения денег
К начислению процентов и удвоению ваших сбережений за определенный промежуток времени могут быть применены некоторые эмпирические правила, одно из которых — «правило семидесяти двух»: для того чтобы узнать время, за которое ваши деньги удвоятся, нужно разделить число «72» на ставку ссудного процента.
Например, при депозите 1 доллар и 4% годовых потребуется примерно 18 лет, чтобы удвоить эту сумму; при 6% — 12 лет; при 8% — 9 лет. Когда проценты начисляются раз в год, 1 доллар при 6% годовых превращается в 2,01 доллара через 12 лет; при 8% доллар дает 2,00 доллара через 9 лет. Следовательно, применение «правила семидесяти двух» дает более или менее достоверные ответы.
Действительно, срок, требующийся для удвоения денег, получаемый по «правилу семидесяти двух», близок к истинному, но не совсем точен. Так, расчет показывает, что при 2% годовых сумма увеличивается вдвое за 36 лет, фактически же на это требуется 35 лет. Если процентная ставка равна 24% в год, по правилу расчета выходит, что денег станет в 2 раза больше через 3 года, в действительности это длится немного дольше — 3,2 года при ежегодном начислении процентов.
Однако если проценты выплачиваются чаще одного раза в год, процесс удвоения суммы занимает немного меньше времени. Возьмем, к примеру, ставку 6% годовых: когда проценты выплачиваются раз в квартал, требуется 11,6 года, чтобы удвоить сумму, против 11,9 лет при ежегодной выплате по «правилу 72» — 12 лет.
Другая эмпирическая закономерность называется «правило 7—10». Согласно этому правилу сумма удваивается через 10 лет при 7% годовых, или через 7 лет при 10% годовых. Если проценты начисляются раз в год, 1 доллар превращается в 1,97 доллара к концу 10 лет при 7% годовых, а через 7 лет при 10% он вырастает до 1,95 доллара. Однако если проценты выплачиваются раз в квартал, 1 доллар по прошествии 10 лет при 7% равен:
F10 = $1*(1+0,07/4)40= $2,002,
а $1 через 7 лет при 10% дает
F7= $1*(1+0,10/4)28= $1,996
Следовательно, «правило 7—10» дает точный результат, если проценты начисляются, раз в квартал, и приблизительный, если — раз в год. Оба рассмотренных эмпирических правила полезно помнить, они дают возможность мысленно производить расчеты, связанные со сложными процентами, т. е. определять срок удвоения капитала при заданной процентной ставке или, установив процентную ставку, подсчитывать время, за которое сумма вырастет вдвое.
Контрольные вопросы:
Что измеряет процентная ставка?
Какая разница между простой и сложной ставкой процента?
Каким образом можно различить номинальную и реальную ставку?
Что подразумевает собой понятие дисконтирования?
Дайте определение чистой приведенной стоимости (NPV)?
В чем заключается важность временной стоимости денег для финансового менеджмента?
Какие способы подсчета временной базы существуют?
Когда разница в способах подсчета дней может оказаться существенной?
Какие виды дисконтирования применяются в вычислениях?
Что является основной областью применения простых процентных и учетных ставок?
В какой области наиболее широко применяются сложные проценты?
Как можно объяснить понятие аннуитета?
Как можно применить эмпирическое правило семидесяти двух?
Что можно измерить используя правило «7-10»?
Глава-4. ДОХОДНЫЙ ПОДХОД К ОЦЕНКЕ ПРЕДПРИЯТИЯ
Метод дисконтирования денежных потоков

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |





