Существуют, однако, два подхода к определению реального дохода, связанные с именами английского экономиста Дж. Хикса и русского математика и экономиста . Согласно Хиксу, разные уровни денежного дохода, обеспечивающие один и тот же уровень удовлетворения, т. е. позволяющие достигнуть одной и той же кривой безразличия, представляют одинаковый уровень реального дохода. Согласно Слуцкому, лишь тот уровень денежного дохода, который достаточен для приобретения одного и того же набора или комбинации товаров, обеспечивает и неизменный уровень реального дохода. Подход Хикса в большей мере соответствует основным положениям порядковой теории полезности, тогда как подход Слуцкого имеет то преимущество, что позволяет дать количественное решение задачи на основе статистических материалов.
2.7. Эффект замены и эффект дохода по Хиксу
Разложение общего эффекта изменения цены на эффект дохода и эффект замены по Хиксу показано на рис. 2.14. Бюджетная линия KL соответствует денежному доходу I и ценам Рх и Ру. Ее касание с кривой безразличия U1 определяет оптимум потребителя Е2 , которому соответствует объем потребления товара в количестве X1. В случае снижения цены Х до Px1 и неизменном денежном доходе I бюджетная прямая займет положение KL1. Она касается более высокой кривой безразличия U2 в точке Е2, которой соответствует потребление товара X в объемеX2.
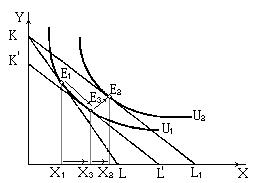
Рис. 2.14. Эффект замены и эффект дохода по Хиксу. (Цена Х снижается).
Таким образом, общий результат снижения цены товара Х выражается в увеличении его потребления с X1 до Х2.
Теперь определим, каким должен был бы быть денежный доход
потребителя, чтобы при изменившемся соотношении цен обеспечить ему прежний уровень удовлетворения. Для этого проведем вспомогательную бюджетную прямую K’L’, параллельную линии KL1 (т. е. отражающую новое соотношение цен), так, чтобы она касалась кривой безразличия U1(т. е. обеспечивала бы прежний уровень удовлетворения). Отметим точку касания Е3 и соответствующий объем потребления товара Х3.
Заметим, что при переходе от первоначального к дополнительному (расчетному) оптимуму (от E1 к E3) реальный доход потребителя не меняется, он остается на прежней кривой безразличия U1. Значит, сдвиг от Е1 к Е3 и характеризует эффект - замены товара Y относительно подешевевшим товаром X. Он равен разности Х3 – X1. Следовательно, эффект дохода составит Х2 - Х3.
Заметим также, что в результате действия эффекта дохода потребление обоих товаров в точке Е2 выше, чем в точке Е3
Такое же разложение общего эффекта может быть выполнено и для случая, когда цена товара повышается.
2.8. Эффект замены и эффект дохода по Cлуцкому
Подход Слуцкого к разложению общего результата изменения цены на эффект дохода и эффект замены отличается от подхода Хикса трактовкой реального дохода. Выделение эффекта дохода достигается определением такого его уровня, который обеспечил бы потребителю возможность приобрести после изменения цен тот же самый набор товаров, что и до изменения, а не сохранить прежний уровень удовлетворения, как это предполагается в модели Хикса.
Поэтому на рис. 2.15 вспомогательная бюджетная прямая K’L’, параллельная KL1, проводится не как касательная к прежней кривой безразличия U1, a строго через точку E1, соответствующую оптимальному набору товаров Х и У при прежнем соотношении цен. Очевидно, она окажется касательной к более высокой, чем U1, кривой безразличия U3, что означает и возможность достигнуть (в случае полной компенсации потребителю - падения его покупательной способности) более высокого уровня удовлетворения, чем при использовании модели Хикса. Таким образом, общий результат повышения цены товара Х (X1 – Х3) разлагается на эффект замены (X1—Х3) и эффект дохода (Х3—Х2). Заметим, что движение от E1 к Е2 происходит не вдоль кривой безразличия, а вдоль вспомогательной бюджетной прямой K’L’.
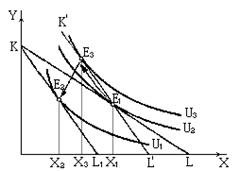
Рис. 2.15. Эффект замены и эффект дохода по Слуцкому. (Цена Х повышается).
Сравнив два подхода, мы видим, что метод Хикса предполагает знание потребительских предпочтений, кривых безразличия, тогда как метод Слуцкого не требует этого, он базируется на наблюдаемых и регистрируемых фактах поведения потребителя на рынке.
3. Теория поведения производителя.
3.1. Производственная функция
Отношения между любым набором факторов производства и максимально возможным объемом продукции, производимой из этого набора факторов, характеризуют производственную функцию. Производственная функция отражает технологическую зависимость между затратами ресурсов и выпуском продукции.
Она характеризуется изоквантой, т. е. различным сочетанием факторов производства при выпуске одного и того же количества продукции, и показывает, что существует много вариантов производства заданного объема продукции. Производственная функция всегда строится для определенной технологической структуры. Улучшение технологии, увеличивающей максимально достижимый объем выпускаемой продукции при любой комбинации факторов, всегда находит отражение в новой производственной функции. Производственная функция может использоваться для определения минимального количества затрат, необходимого для производства любого данного объема товаров.
Если весь набор факторов производства или ресурсов представить как затраты труда, материалов и капитала, производственная функция может быть представлена следующим образом: Q=F(L,K,M),
где Q — максимальный объем продукции, производимой при данной технологии, данном уровне производительности труда L, капитала К и стоимости материалов М.
Модификацией производственной функции является изокванта. Изокванта — кривая, геометрическое место точек, соответствующих всем вариантам производственных факторов, использование которых обеспечивает одинаковый объем выпуска продукции. График, на котором представлен набор изоквант, называют картой изоквант.
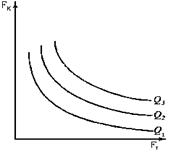 |
Рис2.16. Изокванты.
Где: Q1, Q2, Q3 - различные изокванты,
FК — затраченный труд;
FТ-—используемый капитал.
Специфика анализа деятельности предприятия зависит от периода времени, в течение которого реализуется производственная функция. Различают краткосрочный период (в течение которого производственные факторы остаются фиксированными) и долгосрочный период (отрезок времени, достаточный для внесения изменений во все факторы производства). Американские экономисты Дуглас и Солоу в 20-х годах нашего столетия на основе статистических исследований производства зерна за 100 лет определили вклад таких факторов производства, как труд и капитал, в общий прирост выпуска продукции. Они обнаружили, что увеличение затрат труда на один процент обеспечивает 3/4 прироста выпущенной продукции, а увеличение затрат капитала на один процент дает возможность получить 1/4 прироста выпущенной продукции.
Поскольку эти выводы относились ко всему обществу, то указанные индексы (3/4 и 1/4) назвали агрегатными, а зависимость между выпуском продукции и факторами производства вошла в жизнь под названием агрегатной функции производства Дугласа и Солоу. Таким образом, на основе выводов Дугласа и Солоу были сформулированы так называемые рецепты экономического развития: «вложения в человеческий капитал» — труд — дают больший эффект в увеличении производства, чем рост средств производства (капитал).
Хотя производственные функции различны для разных видов производства, все они обладают общими свойствами.
Во-первых, существует предел для увеличения объёма производства, который может быть достигнут увеличением затрат одного ресурса при прочих равных условиях. Это предполагает, что в фирме при данном количестве станков и производственных помещений существует предел увеличения производства посредством привлечения большего количества рабочих, т. е. прирост объема производства от роста численности занятых будет приближаться к нулю.
Во-вторых, существует определенная взаимная заменяемость факторов производства. При этом взаимозаменяемость факторов производства происходит без сокращения объема производства. Например, эффективен труд работников, если они обеспечены производительным инструментом, однако даже при отсутствии такого инструмента объем может быть увеличен при росте численности занятых. В данном случае происходит замена одного ресурса другим.
3.2. Закон убывающей отдачи.
Закон убывающей отдачи утверждает, что, начиная с определенного момента, последовательное увеличение единиц переменного ресурса (например труда) при фиксированном размере другого ресурса (например капитала или земли) дает уменьшающийся добавочный, или предельный продукт в расчете на каждую последующую единицу переменного ресурса.
3.3. Эффект масштаба
Расширение производства возможно различными путями. При сохранении неизменной технической базы увеличить выпуск можно за счет увеличения применения всех видов ресурсов. В этом случае имеет место увеличение масштабов производства, для его анализа используется понятие отдача от масштаба.
При выборе технически эффективного метода производства увеличение выпуска возможно за счет пропорционального увеличения использования всех производственных ресурсов. Это и есть изменение масштаба производства.
Пусть первоначальное соотношение между выпуском и применяемыми ресурсами описывается производственной функцией:
Q0 = f(K, L). Если мы увеличим объемы применяемых ресурсов (масштаб производства) в k раз, то новый объем выпуска составит:
Q1 = f(kK, kL).
В результате получим:
• постоянную отдачу от масштаба, когда выпуск увеличится также в k раз(Q1=kQ0);
• убывающую отдачу от масштаба, если выпуск увеличится менее чем в k раз(Q1<kQ0);

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 |




