Метод оценки ЭМС для сферического приборного отсека. Метод оценки ЭМС для сферического ПО представляет собой модификацию общего решения электродинамической задачи применительно к резонаторной модели сферического отсека.

Исходные данные для метода те же, что и для цилиндрического приборного отсека. Модели аппаратуры строятся в виде линейных токов, заданных на кривых в сферических координатах.

Решение электродинамической задачи проводится для набора сферических координат и отличается процедурой разделения переменных в уравнениях Гельмгольца.

Учет влияния силового набора оболочки и конструкций крепления аппаратуры. Предложенные выше модели ПО представляли оболочку отсека идеально проводящей, правильной формы, и не учитывали влияния силового набора оболочки и конструкций крепления аппаратуры, являющихся неотъемлемой частью ПО.

Силовой набор является средством обеспечения механической прочности оболочки и представляет собой каркас, вафельный, либо состоящий из стрингеров (продольных стержней) и шпангоутов (поперечных обручей) из определенного материала. Стрингеры могут иметь различное сечение, наиболее типично T-образное. Для шпангоутов типично U-образное сечение.

Аппаратура в отсеке располагается на стойках, подвесах и других конструкциях крепления, выполненных в виде стержней круглого или уголкового сечений.

Силовой набор оболочки и конструкции крепления аппаратуры невелики по сравнению с отсеком и устройствами, так что решающего влияния на структуру и величину ЭМП в ПО они не оказывают. Однако, представляя собой определенным образом расположенную в отсеке массу диэлектрика или проводника (в зависимости от материала), безусловно, изменяют ЭМП. Предлагается рассматривать подобные конструкции как тела, возмущающие электромагнитное поле в малом объеме отсека правильной формы.

В зависимости от электродинамической модели отсека и геометрии (формы, расположения) возмущающей конструкции можно рассмотреть следующие ситуации.

Метод для резонаторной модели отсека. Приборный отсек моделируется полым резонатором V с однородным заполнением и идеально проводящей оболочкой S.

Пусть известны собственные колебания и собственные частоты внутри невозмущенного резонатора. Они связаны уравнениям Максвелла:

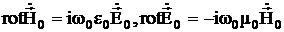, (3.28)

и граничным условием .

При заполнении резонатора диэлектриком с параметрами возмущенное поле будет определяться уравнениями Максвелла на сдвинутой собственной частоте :

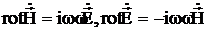(3.29)

с теми же граничными условиями. Изменение собственной частоты при введении в резонатор диэлектрика или магнетика:

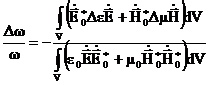, (3.30)

где:

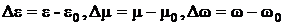(3.31)

При малом объеме тела вне этого объема можно пренебречь возмущением:

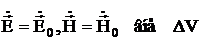(3.32)

Тогда:

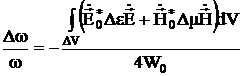, 3.33)

где

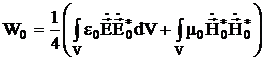(3.34)

- энергия, запасенная в невозмущенном резонаторе.

Для рассматриваемых конструкций характерна вытянутая форма. При этом, если вектор параллелен длинной оси, то , а если перпендикулярен, то 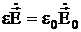. Аналогичные соотношения справедливы и для магнитного поля.

Если материал конструкций – диэлектрик с потерями, т. е. характеризуется проницаемостями:

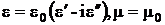, (3.35)

то собственные частоты возмущенного и невозмущенного резонаторов являются комплексными:

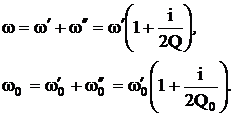(3.36)

Если конструкция находится в области с , то для нее справедливы выражения:

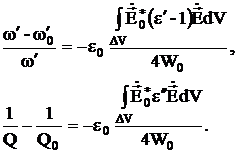(3.37)

Для магнетиков следует произвести замену , .

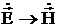Для силового набора, непосредственно примыкающего к оболочке отсека, удобно считать, что вектор перпендикулярен границе, а вектор параллелен ей. Тогда внутри объема, занимаемого телом, 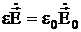, и сдвиг частоты определяется выражением:

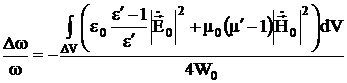(3.38)

Метод для волноводной модели отсека. Приборный отсек моделируется отрезком бесконечного волновода, заключенным между двумя экранами. Теория возмущений рассматривает два случая: возмущение регулярного волновода и возмущение волновода телом, нарушающим регулярность.

Рассмотрим сначала первый случай.

К телам, не нарушающим регулярность волновода, можно отнести продольные элементы силового каркаса (стрингеры) и ориентированные вдоль оси z достаточно длинные отрезки арматуры.

Пусть поле в невозмущенном регулярном волноводе, заполненном продольно-однородной средой с параметрами , и поле в возмущенном волноводе представляются в виде:

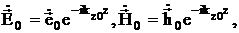(3.39)

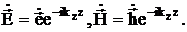(3.40)

где: 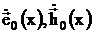- векторные функции, определенные в поперечном сечении волновода S;

x - набор координат в поперечном сечении;

- проекция волнового вектора.

Тогда изменение волнового числа определяется выражением:

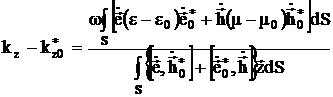. (3.40)

Так как возмущающее тело занимает малую часть поперечного сечения , то вне этой части положим , и получим:

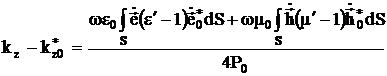, (3.41)

где – мощность невозмущенной волны, равная знамена

Для электрических конструкций, параллельных оси волновода изменение вещественной и мнимой частей волнового числа составит:

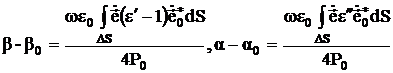(3.42)

Для конструкций, непосредственно примыкающих к оболочке можно считать 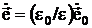, 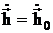и поэтому:

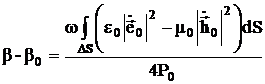(3.43)

Выражения для магнетиков получаются из (3.42) и (3,43) подстановкой , .

Ко второму случаю относятся все элементы силового набора и арматуры, нарушающие регулярность волновода. Это шпангоуты и вафельный каркас, а также основные элементы крепления аппаратуры Теория возмущений предлагает рассматривать их как рассеивающие элементы, характеризующиеся многомодовыми коэффициентами отражения и ставить задачу волноводной дифракции на однородном теле.

3.1.2. Разработка метода интегральной оценки ЭМС в приборном отсеке.

В предыдущих методах оценки ЭМС при рассмотрении отсека задача подразделялась на задачу излучения в идеальной оболочке и последующий учет реальности рассеивателей, таких как силовой набор оболочки и конструкции крепления аппаратуры. Однако можно предложить комплексный подход, рассматривая отсек как интегральную систему.

Модель приборного отсека как излучающей системы в присутствии рассеивающих элементов. Определим приборный отсек объема V, ограниченный поверхностью S, как излучающую систему в присутствии рассеивателей. Излучающими элементами являются приборы и кабели, рассеивающими - оболочка отсека с силовым набором, конструкции крепления аппаратуры и сами устройства.

Пусть в отсеке заключены А излучателей, т. е. приборов и кабелей. Каждый из них в отдельности можно описать собственными токами , используя спектральные характеристики помехообразования, полученные при экспериментальной аттестации их, например, в ТЕМ-камере. По данным характеристикам на основании принципа эквивалентных токов строятся электродинамические модели устройств - устройства заключаются в поверхности произвольной формы , на которых задаются поверхностные плотности электрического и магнитного токов. Для удобства описания комплексные характеристики сводятся к амплитудно-фазовому распределению .

Будучи совместно помещены в отсек, излучатели наводят друг на друге и на рассеивающих элементах поверхностные токи, амплитудно-фазовые распределения которых на поверхностях и рассеивателях, обоpзначим и соответственно.

Рассеиватели для удобства краткости обозначений будем характеризовать суммарной поверхностью .

В результате на поверхностях, ограничивающих излучатели, получим полные токи:

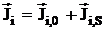. (3.44)

Аналогичным образом, представим допустимые уровни помех для каждого устройства амплитудно-фазовым распределением эквивалентного тока на поверхности .

В качестве модели отсека предлагается система излучающих элементов, ограниченных произвольными поверхностями и характеризующихся амплитудно-фазовым распределением тока 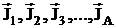на этих поверхностях, в присутствии идеально проводящих рассеивающих элементов, ограниченных суммарной поверхностью и характеризующихся наведенным током (рис. 3.2).

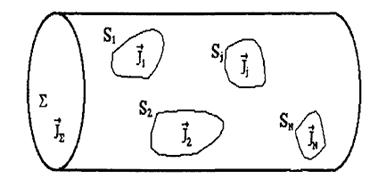
Рис. 3.2. Модель приборного отсека как излучающей системы в присутствии рассеивающих элементов.

В терминах данной модели критерий электромагнитной совместимости в отсеке можно представить как:

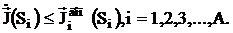(3.45)

т. е. недопустимость превышения полными токами на поверхностях, охватывающих устройства, токов, эквивалентных допустимым уровням ЭМП для набора штатных ситуаций в полосе частот.

Метод оценки ЭМС. В состав полных токов на поверхностях, охватывающих излучатели, входят неизвестные наведенные токи . Задача оценки ЭМС в приборном отсеке с помощью предложенной модели отсека поэтому заключается в определении токов , по ним - полных токов и оценке ЭМС по критерию (3.45).

Для нахождения полных токов воспользуемся результатами теории синтеза устройств. Известна система интегральных уравнений:

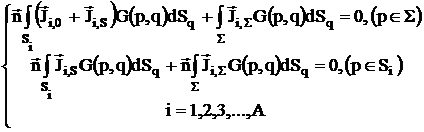(3.46)

Здесь - функция Грина, q - точка в области источников, p – точка наблюдения.

Оценка для электрического и магнитного полей проводится отдельно, т. к. уравнения Гельмгольца, определяющие векторные электрический и магнитный потенциалы независимы.

В результате решения системы уравнений (3.46) определяются токи, заведенные на излучателе и полная плотность тока (3.44), характеризующая электромагнитную обстановку в месте расположения i-го устройства для длины волны и некоторого штатного состояния. ЭМС оценивается по критерию (3.43).

Метод оптимизации ЭМС. На основе предложенной модели по найденным полным токам , можно произвести оптимизацию компоновки приборного отсека относительно электромагнитной совместимости.

Снова воспользуемся результатами теории синтеза излучающих систем. Можно провести интегральную оценку связи между элементами излучающей системы, образовав с помощью предварительно определенных полных на излучателях и наведенных на рассеивателях токов функционал:

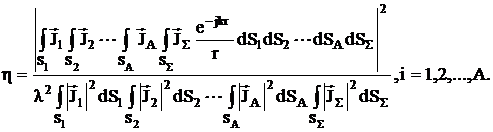(3.47)

Функционал определен на множестве излучателей и рассейвателей, т. е. на множестве поверхностей, охватывающих излучатели и рассеиватели.

3.2. Предварительная оценка ЭМС спутниковых систем.

Спутниковые навигационные системы. Термины и определения.

Альманах - совокупность данных характеризующих эфемериды всех спутников системы.

Восходящий узел орбиты - точка, в которой спутник переходит из южного полушария в северное.

Конфигурация созвездия спутников - расположение спутников системы в пространстве, описываемое параметрами орбит и смещением спутников на орбитах.

Наклонение орбиты - двухгранный угол между плоскостью орбиты и плоскостью экватора, отсчитываемый от плоскости экватора против хода часовой стрелки для наблюдателя, находящегося в точке восходящего узла.

Система радионавигационная спутниковая - система определения ПМЛА и скорости потребителя, основанная на основе искусственных спутников Земли в качестве РНТ.

Угол зенитный - угол между вертикалью в месте наблюдения и направлением на спутник.

Эфемериды - значения координат искусственного спутника Земли в геоцентрической системе координат, рассчитанные для фиксированных моментов по результатам прогнозирования движения этого спутника.

Назначение и типы спутниковых навигационных систем. Спутниковые навигационные системы (СНС) относятся к классу многопозиционных РНС и предназначены для определения пространственного местоположения и вектора скорости потребителей в пределах всей (или большей части) поверхности земли (глобальные системы). Возможны также региональные СНС, обслуживающие ограниченные территории. Для авиационных целей представляют интерес СНС второго поколения, обеспечивающие непрерывное и практически мгновенное определение ПМЛА. Для СНС второго поколения выделены частоты 960...1215 и 1535...1660 МГц, а также резервные диапазоны 4200...4400, 5000...5250 и 15400МГц.

Основа СНС - сеть («созвездие») навигационных искусственных спутников Земли (НИСЗ), выполняющих функцию опорных РНТ, относительно которых измеряются НП. Конфигурация созвездия и число НИСЗ выбираются из условий получения требуемой зоны действия СНС, избыточного числа видимых спутников в точке приёма (для выбора подходящего по геометрическому фактору рабочего созвездия), удобства управления системой и наименьшего влияния возмущающих движение спутников факторов. Высоты орбит наиболее известных СНС около 20000 км (период обращения спутника 12 ч). Для описания созвездий используют запись , где А, В и С - число орбит, количество спутников на каждой орбите и период обращения спутника соответственно. Спутники служат источниками навигационных сигналов и служебной информации. В некоторых системах НИСЗ используются в качестве ретрансляторов навигационных сигналов. Для снабжения спутников навигационной информацией, контроля параметров орбит, состояния аппаратуры НИСЗ и управления системой предусматриваются наземные командно-измерительные комплексы (КИК). Местоположение потребителя, как правило, определяется его собственной аппаратурой, процессор которой позволяет в ряде СНС найти не только ПМЛА, но и скорость потребителя, а также определить точное время.

Навигационные параметры в СНС - обычно квазидальность и квазискорость, так как результаты их измерения включают неизвестный сдвиг ДТ шкалы времени потребителя относительно системного времени. Для определения НП требуется элементарное созвездие из четырех спутников, которое является основным рабочим звеном большинства СНС второго поколения.

Типы СНС (приведены в таблице) отличаются конфигурацией созвездий, местом определения координат спутников, местом формирования навигационного сигнала, режимом работы АН (пассивный или активный в зависимости от отсутствия или наличия передатчика) и способом разделения сигналов НИСЗ. Системы второго поколения находятся на этапе ввода в эксплуатацию.

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9