При этом мощность шума на выходе данного фильтра при отсутствии ЭМ помеховых воздействий равна произведению 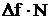 , где N – спектральная плотность шума в приемном канале.
, где N – спектральная плотность шума в приемном канале.
В случаях, когда спектр помехового сигнала в функции от частоты постоянный, т. е. равномерный, близкий к шумовому, что может быть, когда в рассматриваемых, в частности, РЛС с импульсно-пачечным сигналом, опорные генераторы обладают типовыми значениями нестабильности частоты, влияние помехового сигнала может быть принято при данном рассмотрении не отличающимся от влияния того же уровня мощности шума. Зависимостью (2.11) в этом случае можно пользоваться при простой замене в (2.13) мощности шума ![]() суммой
суммой ![]() .
.
По значениям матрицы ![]() в (2.10) при этом следует записать той же структуры матрицу
в (2.10) при этом следует записать той же структуры матрицу ![]() , где каждый элемент
, где каждый элемент ![]() - результат аддитивного суммирования мощности собственного шума
- результат аддитивного суммирования мощности собственного шума ![]() и мощности помехи
и мощности помехи ![]() . В свою очередь при минимальном граничном уровне
. В свою очередь при минимальном граничном уровне ![]() для сигнала от цели, обеспечивающем в соответствии с (2.11), (2.13) значения требуемых обнаруживаемых характеристик D и при отсутствии постороннего помехового воздействия, для каждого элемента матрицы
для сигнала от цели, обеспечивающем в соответствии с (2.11), (2.13) значения требуемых обнаруживаемых характеристик D и при отсутствии постороннего помехового воздействия, для каждого элемента матрицы ![]() может быть записана обозначенная
может быть записана обозначенная ![]() разность:
разность:
![]() (2.14)
(2.14)
при выражении всех величин в дБ по отношению к мощности шума.
Значения ![]() при каждом i и j в соответствии с определениями, сделанными выше, представляют собой отношение мощности
при каждом i и j в соответствии с определениями, сделанными выше, представляют собой отношение мощности ![]() к сумме мощностей
к сумме мощностей ![]() . В связи с этим, и с учетом приведенных выше оговорок о равномерном спектре сигнала помехового ЭМ воздействия на выходе приемного канала, значения
. В связи с этим, и с учетом приведенных выше оговорок о равномерном спектре сигнала помехового ЭМ воздействия на выходе приемного канала, значения ![]() могут быть приняты за величину
могут быть приняты за величину ![]() в соответствии с (2.13) и из уравнения (2.11), либо из рис.2.2, для каждого
в соответствии с (2.13) и из уравнения (2.11), либо из рис.2.2, для каждого ![]() для заданной вероятности обнаружения D может быть найдена вероятность ложной тревоги
для заданной вероятности обнаружения D может быть найдена вероятность ложной тревоги ![]() , обозначенная
, обозначенная ![]() в (2.7). При этом само выражение (2.7) после корректировки обозначений компонент будет иметь вид:
в (2.7). При этом само выражение (2.7) после корректировки обозначений компонент будет иметь вид:
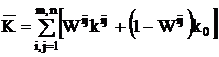 (2.15)
(2.15)
Подстановка в (2.15) найденных значений ![]() , а также из (2.9) значений
, а также из (2.9) значений ![]() определит результирующую величину вероятности ложной тревоги
определит результирующую величину вероятности ложной тревоги ![]() в приемном канале, обуславливаемую сигналами помехового ЭМ воздействия по боковым лепесткам ДН антенны от параллельно работающей РЛС для указанной области углов
в приемном канале, обуславливаемую сигналами помехового ЭМ воздействия по боковым лепесткам ДН антенны от параллельно работающей РЛС для указанной области углов ![]() ,
, ![]() в целом, в окрестности
в целом, в окрестности ![]() ,
, ![]() и
и ![]() ,
, ![]() при условии равной вероятности установки различных значений
при условии равной вероятности установки различных значений ![]() ,
, ![]() в этой области.
в этой области.
2.3. Аналитическая оценка интермодуляционных помех.
Известен геометрический метод определения вероятности возникновения по частотным условиям различных типов радиоприемной интермодуляции. Для задач КВ приема в произвольных диапазонах с интенсивными сосредоточенными по спектру излучениями имеется также необходимость в аналитическом (непереборном) описании всего множества сотен и тысяч каналов, потенциально опасных в отношении данного вида помех.
Рассмотрим последовательность одинаковых по ширине спектра каналов с номерами от –Lн до L, L≥1, L≥1, определяемые частотой настройки f0 в общем диапазоне ![]() (рис.2.3) при
(рис.2.3) при ![]() .
.
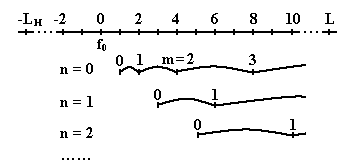
Рис.2.3. Последовательность одинаковых по ширине спектра каналов
с номерами от –Lн до L
В каналах с частотой выше f0 выделим последовательности nm со своими индексами так, чтобы номинальные частоты элементов каждой из них соответствовали условию:
![]() (2.16)
(2.16)
Переход к представлению на рис.2.4 позволит изображать исходные номера каналов в узлах сетки координат и оперировать целочисленными точками заданной области квадранта, ограниченной кривой:
![]() (2.17)
(2.17)
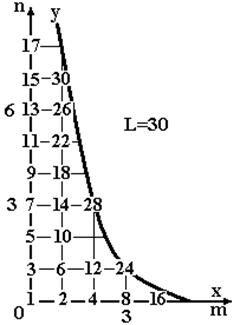
Рис.2.4. Исходные номера каналов в узлах сетки координат и целочисленные точки области квадранта
Из графика следует, что оценкой количества каналов, не имеющих ни одной соседней (по горизонтали) целочисленной точки для образования ИМ пары (рис.2.5) может служить:
![]() (2.18)
(2.18)
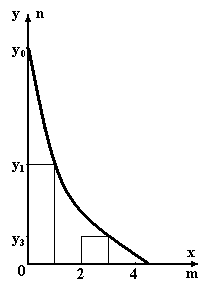
Рис.2.5. Оценкой количества каналов
Объединение остальных каналов осуществляется следующим образом. При ![]() ,
, ![]() , есть только первые (с
, есть только первые (с ![]() ,
, ![]() ) пары подпоследовательностей в количестве:
) пары подпоследовательностей в количестве:
![]() (2.19)
(2.19)
При ![]() ,
,![]() к ним добавляются
к ним добавляются ![]() вторых пар, составляя:
вторых пар, составляя:
![]() ;
;
при 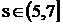 - соответственно:
- соответственно:
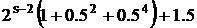 и т. д.
и т. д.
Выведем общую зависимость по точкам 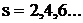 с учетом суммы геометрической прогрессии
с учетом суммы геометрической прогрессии 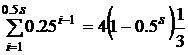 в виде:
в виде:
![]() (2.20)
(2.20)
Аналогично, описывая каналы к частотами нижеf0, находим оценку количества для всего диапазона:
![]() (2.21)
(2.21)
Ее максимум 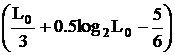 находится в середине диапазона
находится в середине диапазона ![]() , незначительно отличаясь от минимума в конечных точках
, незначительно отличаясь от минимума в конечных точках 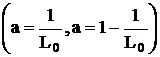 на величину
на величину 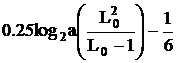 .
.
Для практически важных 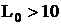 можно считать, что независимо от положения канала настройки, частотные условия существуют для возникновения
можно считать, что независимо от положения канала настройки, частотные условия существуют для возникновения ![]() пар каналов.
пар каналов.
Данные оценки могут быть также использованы для определения обобщенного динамического диапазона приемника с учетом его нелинейных и селективных характеристик.
Если стандартное измерение ИМ динамического диапазона D (рис.2.6) двухсигнально, то при показателе преселекции ![]() и потенциальном наличии свойственных данному устройству N суммарная мощность помех на выходе приемника на
и потенциальном наличии свойственных данному устройству N суммарная мощность помех на выходе приемника на 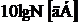 больше, а обобщенный параметр D0 соответственно меньше:
больше, а обобщенный параметр D0 соответственно меньше:
![]() (2.22)
(2.22)
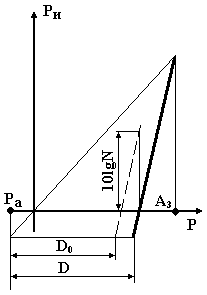
Рис.2.6. Стандартное измерение ИМ динамического диапазона
Используя далее статистические характеристики входных сигналов, считаем, что вероятность действия не сосредоточенных помех в каждом канале равна p. Найдем оценку наиболее вероятного количества ![]() случаев появления некоторого события последовательно в двух любых испытаниях серии из k одинаковых (по вероятности события р) испытаний при условии, что события в каждом испытании может быть отнесено только к одному случаю (при
случаев появления некоторого события последовательно в двух любых испытаниях серии из k одинаковых (по вероятности события р) испытаний при условии, что события в каждом испытании может быть отнесено только к одному случаю (при ![]() данная оценка эквивалентна вероятности случая). Так:
данная оценка эквивалентна вероятности случая). Так:
![]()
В серии из четырех испытаний случай происходит один раз с вероятностью ![]() , дважды – с
, дважды – с ![]() и
и ![]() . Аналогично
. Аналогично ![]() и т. д.
и т. д.
Рассматривая размещения с повторениями из двух элементов по К, выведем степенной знакопеременный ряд:
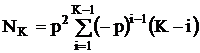 , (2.23)
, (2.23)
или:
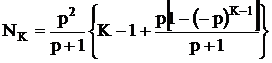 (2.24)
(2.24)
Целочисленная модель позволяет выделять группы серий. Например (рис.2.7), в общем виде действуют ![]() серий из двух испытаний,
серий из двух испытаний, ![]() - из трех испытаний и т. д., а самая длинная серия с
- из трех испытаний и т. д., а самая длинная серия с 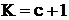 , где
, где ![]() , всего одна.
, всего одна.
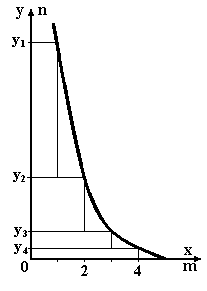
Рис.2.7. Целочисленная модель
Так, при ![]() действует серия из пяти испытаний с
действует серия из пяти испытаний с ![]() ,
,![]() четверок с
четверок с ![]() и т. д., что дает сумму:
и т. д., что дает сумму:
![]() .
.
Обобщая сказанное, получаем оценку наиболее вероятного количества пар каналов в диапазоне с равномерным распределением сосредоточенных помех:
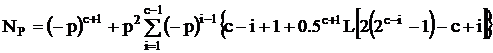 , (2.25)
, (2.25)
которая после преобразований упрощается с достаточной для практики точностью:
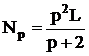 . (2.26)
. (2.26)
Вводя величину средней мощности в занятых каналах, определяем ухудшение реальной способности устройств принимать слабые сигналы при интермодуляции помех, которые в пределах некоторой максимальной расстройки от f0 являются одинаково опасными также и по внутренним селективным и нелинейным свойствам тракта – степень ослабления до входа основного нелинейного элемента и производимому в нем ИМ отклику. Если непосредственно на частоте настройки излучений нет, то для компенсации приведенных ко входу приемника погрешностей ИМ помех:
![]() (2.27)
(2.27)
и шумов, собственных и антенных, ![]() при сохранении значения критерия
при сохранении значения критерия
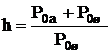 (2.28)
(2.28)
чувствительности надо увеличить минимально необходимый сигнал до
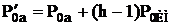 , (2.29)
, (2.29)
где 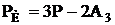 ,
,
![]() (рис.2.6),
(рис.2.6),
![]() ,
,
![]() ,
,
![]() .
.
2.4. Выбор показателей эффективности и анализ методов частотных присвоений при решении задачи ЭМС в сетях электросвязи.
2.4.1. Анализ и выбор показателей эффективности,
используемых для частотных присвоений.
Важнейшей задачей системы автоматизированного распределения частотных присвоений в передающей сети радиовещания является оптимальное распределение частотных каналов передатчикам сети. Под оптимальностью распределения понимается минимизация взаимных помех, т. е. обеспечение наилучшего использования технических ресурсов передающей сети в условиях ограничений наложенных на использование частотного спектра. Распределение частот между передатчиками, в конечном счёте, сводится к рассмотрению всевозможных парных частотных присвоении, когда для двух конкретных передатчиков требуется решить вопрос об оптимальности или не оптимальности присвоения им взаимно мешающих частотных каналов. Следовательно, необходим показатель эффективности, на основании которого должна производиться оценка каждого такого присвоения.
Используемая напряженность поля. Используемая напряженность поля в точке установки передатчика - есть минимальная требуемая напряженность поля сигнала, при которой помеха превышает величину защитного отношения:
![]() , (2.30)
, (2.30)
где: ![]() - напряженность поля помехи, создаваемая в точке установки передатчика, дБ;
- напряженность поля помехи, создаваемая в точке установки передатчика, дБ;
![]() - требуемое защитное отношение, дБ.
- требуемое защитное отношение, дБ.
Имеется два передатчика, требуется определить возможность присвоения обоим одного и того же частотного канала. Для этого один принимаем за помеху и считаем его напряженность поля в точке установки другого передатчика. Учитывая защитное отношение, найдем искомую ![]() . Чтобы дать ответ на вопрос о возможности присвоения этим передатчикам одного частотного канала, необходимо сравнить полученную
. Чтобы дать ответ на вопрос о возможности присвоения этим передатчикам одного частотного канала, необходимо сравнить полученную ![]() с некоторым оптимумом используемой напряженности.
с некоторым оптимумом используемой напряженности.
Если рассчитанная ![]() лежит в допустимых пределах отклонения от оптимального значения, то показатель дает положительный ответ. Предполагается оптимум используемой напряженности определять экспериментально, исходя из конкретных расстояний между передатчиками, обладающими определенными техническими параметрами
лежит в допустимых пределах отклонения от оптимального значения, то показатель дает положительный ответ. Предполагается оптимум используемой напряженности определять экспериментально, исходя из конкретных расстояний между передатчиками, обладающими определенными техническими параметрами ![]() и
и ![]() , и диапазоном их работы. Используемая напряженность поля показатель эффективности парный, поэтому он рассчитывается в точке установки обоих передатчиков, когда другой считается помехой. Возможность присвоения частотного канала оценивается по передатчику, находящемуся в худших условиях с точки зрения помехи.
, и диапазоном их работы. Используемая напряженность поля показатель эффективности парный, поэтому он рассчитывается в точке установки обоих передатчиков, когда другой считается помехой. Возможность присвоения частотного канала оценивается по передатчику, находящемуся в худших условиях с точки зрения помехи.
Достоинства этого критерия в простоте расчетов. Зная расстояние между передатчиками R и их технические параметры (![]() ,
,![]() ) можно определить напряженность поля помехи:
) можно определить напряженность поля помехи:
![]() , (2.31)
, (2.31)
где: 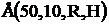 - напряженность поля помехи на расстоянии R от мешающего передатчика, определяется по специальным номограммам, называемым кривыми распространения, дБ;
- напряженность поля помехи на расстоянии R от мешающего передатчика, определяется по специальным номограммам, называемым кривыми распространения, дБ;
![]() - эффективная излучаемая мощность передатчика помехи, дБ.
- эффективная излучаемая мощность передатчика помехи, дБ.
Учитывая защитное отношение в зависимости от вида исследуемой помехи, находим:
![]() (2.32)
(2.32)
Но для этого показателя эффективности сложно определять его оптимальное значение и он не дает количественной оценки оптимальности присвоения частотного канала.
Таким образом, показатель эффективности «используемая напряженность поля в точке установки передатчика» удобно использовать для первичного экспресс-анализа ситуации, т. е. когда необходимо отобрать все частоты, которые возможно присваивать в данном пункте. А оптимальность присвоения того или иного частотного канала предлагается оценивать с помощью одного из ниже описываемых показателей эффективности.
Координационное расстояние. Рассмотрим два передатчика, которые могут создавать взаимные помехи. Минимальное расстояние между ними, при котором их взаимное влияние не уменьшает радиус зоны вещания передатчиков по сравнению с максимальной, назовем координационным расстоянием и обозначим ![]() , (см. рис.2.8).
, (см. рис.2.8).

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 |




