За его пределами вершин, смежных с данной, существовать не может (рис.2.19). В однородной регулярной сети радиус такого круга одинаков для каждой вершины. Для неоднородной, нерегулярной сети радиус такого круга можно определить для максимальных параметров передающей станции и считать его неизменным для всей сети.
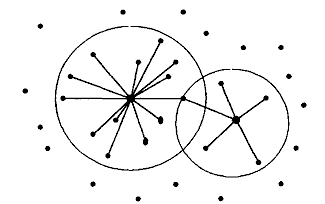
Рис.2.19. Граф реальной передающей сети
Учитывая такое представление графа передающей сети радиовещания, сколько бы не наращивался граф такой сети, число смежных вершин для каждой не может превышать максимальной степени Δ(G) вершин графа G.
При решении задачи о раскраске вершин графа необходимо определить смежность пар вершин (или влияние пар передатчиков друг на друга), т. е. необходимо определить, создают ли два данных передатчика помехи друг другу. Решение этой задачи позволяет автоматически определить граф сети радиовещания.
3. Модели оценки ЭМС
3.1. Модели ЭМО и оценка ЭМС РЭО в приборных отсеках воздушного судна.
Современное состояние техники, охват радиоэлектронными средствами всех отраслей человеческой жизни, постоянное усложнение радиотехнических систем выводит на одно из первых мест задачу обеспечения надежности аппаратуры, одним из критериев которой выступает ее электромагнитная совместимость (ЭМС). В таких отраслях науки, как космическое и авиационное кораблестроение, где постоянно растущая насыщенность радиотехнических систем, в частности, приборных отсеков летательных аппаратов, сложной и дорогостоящей радиоэлектронной аппаратурой сочетается с особо жесткими требованиями к безотказности работы, проблема комплексной оценки внутрисистемной ЭМС приобретает особую актуальность.
Объектом исследований являются приборные отсеки летательных аппаратов. Предметом исследований является внутрисистемная ЭМС приборных отсеков.
Приборные отсеки имеют такие летательные аппараты (ЛА), как: космические корабли; космические станции; искусственные спутники, предназначенные для научных исследований, метеорологических наблюдений и связи; крупный авиатранспорт.
Приборный отсек (ПО) представляет собой замкнутый объем, ограниченный оболочкой, в основном, правильной геометрической формы, выполненной одно - или многослойной, из металлических сплавов или композитных материалов, подкрепленной с внутренней стороны силовыми конструкциями (продольными, поперечными, вафельными, их комбинациями). В оболочке могут быть шлюзы, смотровые окна. В объеме расположены с помощью крепежных конструкций блоки приборов и кабели.
Проблема ЭМС возникает из-за совместной работы аппаратуры, передающей и принимающей энергию как по основному каналу, так и помимо него.
Внутри аппарата возникают помехи, которые можно подразделить на: кондуктивные и излучаемые, последние выступают в виде электростатических и переменных электромагнитных полей.
Основным источником электромагнитных помех являются блоки приборов, обладающие собственным радиоизлучением за счет поверхностных токов, появляющихся из-за утечки в местах стыковок, разъемов, недостаточной герметичности и наведения извне. Дополнительными источниками излучений служат подводящие кабели. Эти помехи вызываются целиком особенностями аппаратуры. Другие же виды помех возникают во время полета летательного аппарата, вызываясь внешними по отношению к приборному отсеку ЛА факторами, осложняют электромагнитную обстановку (ЭМО).
Электрические поля вызываются в основном электризацией летательного аппарата, основными причинами возникновения которой является взаимодействие ЛА с магнитосферной плазмой. Интенсивные потоки электронов высокоэнергетичных электронов образуют отрицательный ток на ЛА, приводящий к зарядке аппарата до высоких отрицательных потенциалов, что при плохой его поверхностной и объемной электропроводности ведет к резко неоднородному распределению заряда по поверхности и возможности пробоя оболочки отсека. Потоки электронов и жесткого космического излучения могут проникать и внутрь аппарата и приводить к появлению на электрически изолированных деталях конструкции и на диэлектриках зарядов, величины которых достаточны для пробоя диэлектриков и изолирующих покрытий [42]. Разрядные явления между неоднородно заряженными частями ЛА помимо прямого разрушения электроники (в случае достаточно большой их мощности) создают интенсивные электромагнитные помехи (уже и при малой мощности) и нарушают работу электронных устройств. При прохождении ЛА через атмосферу Земли нарушение работы аппаратуры может вызываться и разрядами молний.
Во время работы радиоэлектронной аппаратуры (РЭА) также возникают импульсные кондуктивные электромагнитные поля (ЭМП), которые прямым путем и через паразитные емкости связи провод-корпус, проходя через РЭА, попадают на вход функциональной аппаратуры и нарушают ее работу.
Особенность проблемы ЭМС в приборных отсеках летательных аппаратов заключается в следующем:
1) Аппаратура размещается в отдельном, герметичном приборном отсеке. Оболочка ПО может быть неоднородной и оказывает влияние на ЭМС радиоэлектронной аппаратуры в отсеке.
2) Необходимость в компактном размещении значительного числа блоков устройств приводит к возникновению взаимных помех и повышению их восприимчивости к помехам. Плотность компоновки и тенденции к интеграции аппаратуры заметно усложняют задачу, перемещая фокус с дальней зоны излучения на ближнюю.
3) В состав комплексов аппаратуры нередко входят приборы и блоки приборов, не удовлетворяющие нормам ЭМС по результатам
экспериментальной аттестации согласно стандартам, что ухудшает
электромагнитную обстановку в отсеке.
4) Блоки радиоэлектронных устройств не имеют стандартной геометрии и соединены между собой кабелями сложной формы.
5) Задача оценки ЭМС осложняется многопараметровым характером
информации, обрабатываемой в устройствах.
6) Перекрытие временных и частотных интервалов работы приводят к тому, что устройства работают в различных областях частотной оси, занимая в комплексе полосу частот, которая постоянно расширяется. В настоящее время увеличивается использование гигагерцового диапазона, особенно при работе бортовых систем искусственных спутников Земли.
7) Использование в последнее время более легких композиционных
материалов вместо традиционных алюминия и титана уменьшает
экранирующий эффект и создает дополнительные трудности обеспечения ЭМС.
Среди разработанных к настоящему времени аспектов проблемы ЭМС большая часть применима как к наземным радиотехническим комплексам, так и к бортовой аппаратуре.
3.1.1. Разработка моделей приборных отсеков и методов
комплексной оценки ЭМС.
Модель приборного отсека в общей постановке задачи является довольно общей и допускает дальнейшую конкретизацию, что повышает ее мощность применительно к определенным приборным отсекам. В зависимости от представления приборного отсека той или иной моделью общий электродинамический подход модифицируется в различные по своим возможностям, границам применимости, уровню точности, имеющимся исходным данным, вычислительным затратам и трудоемкости методы оценки ЭМС в приборном отсеке.
Разработка резонаторных моделей и метода оценки ЭМС. Характерность правильных геометрических форм (цилиндр, сфера, тор) позволяет в случае однородной оболочки представить отсек резонатором.
Резонаторная модель приборного отсека. Для приборного отсека каждой формы электродинамическая модель будет своя, построенная на соответствующем резонаторе.
В общем виде модель представляет собой резонатор определенной правильной формы, объема V0, с проводящей поверхностью S, заполненный
изотропной средой с диэлектрической ![]() и магнитной
и магнитной ![]() проницаемостями, в котором расположены излучатели и рассеиватели, и характеризующийся добротностью как функцией частоты
проницаемостями, в котором расположены излучатели и рассеиватели, и характеризующийся добротностью как функцией частоты ![]() .
.
Форма оболочки отсека определяет систему координат, в которой ведется решение электродинамической задачи, и набор собственных функций оператора Лапласа в данной системе координат, описывающий электромагнитное поле внутри резонатора.
Приборный отсек цилиндрической формы моделируется цилиндрическим резонатором длины L, радиуса R, в котором на кривых ГЭ, ГМ, заданных в цилиндрической системе координат, определены линейные эквивалентные токи ![]() .
.
Приборный отсек сферической формы моделируется сферическим резонатором радиуса R, в котором на кривых ГЭ, ГМ, заданных в сферической системе координат, определены линейные эквивалентные токи ![]() .
.
Задача в случае тороидального отсека несколько усложняется. Пусть а - внутренний радиус тора, а R - его наружный радиус (рис. 3.1). Если условие R>>a не выполняется, то необходимо проводить разделение переменных в уравнении Гельмгольца в специальных тороидальных координатах, что очень существенно осложняет решение.
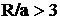 . (3.1)
. (3.1)
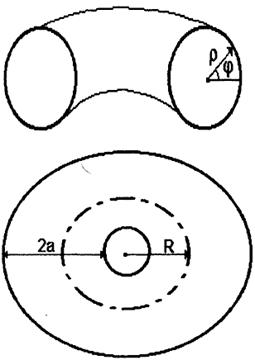
Рис. 3.1. Тороидальный приборный отсек.
В реальном случае задача нахождения поля близка к задаче в цилиндрическом резонаторе. Различие заключается лишь в том, что вместо граничных условий на торцах цилиндра ставится условие периодичности поля по координате z вдоль оси цилиндра с периодом ![]() R. Линейную координату z удобно заменить угловой координатой:
R. Линейную координату z удобно заменить угловой координатой:
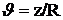 . (3.2)
. (3.2)
Две другие координаты ![]() и
и ![]() - обычные полярные координаты.
- обычные полярные координаты.
Тороидальный приборный отсек при наложенных ограничениях (3.1) моделируется цилиндрическим резонатором длины 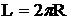 , радиуса a, в Котором на кривых ГЭ, ГМ, заданных в модифицированной системе координат
, радиуса a, в Котором на кривых ГЭ, ГМ, заданных в модифицированной системе координат ![]() , определены линейные эквивалентные токи
, определены линейные эквивалентные токи ![]() , и для которого накладывается условие периодичности вдоль оси отсека.
, и для которого накладывается условие периодичности вдоль оси отсека.
Метод оценки ЭМС для цилиндрического приборного отсека. Метод оценки ЭМС для цилиндрического ПО представляет собой модификацию общего решения электродинамической задачи применительно к резонаторной модели цилиндрического отсека.
Исходными данными для метода также являются экспериментальные спектральные характеристики помехообразования приборов и кабелей, на основании которых строятся модели аппаратуры в виде линейных токов, заданных на кривых в цилиндрических координатах.
Для решения электродинамической задачи необходимо найти явный вид разложения для векторных потенциалов в цилиндрическом резонаторе. Теперь x заменяется набором цилиндрических координат ![]() а индексы i, j, l, принимая значения 1, 2, 3, перечисляют цилиндрические координаты векторов, т. е.
а индексы i, j, l, принимая значения 1, 2, 3, перечисляют цилиндрические координаты векторов, т. е. ![]() .
.
В цилиндрической системе координат оператор Лапласа в векторной функции ![]() , смешивает компоненты
, смешивает компоненты ![]() и
и ![]() , поэтому можно записать связанную систему уравнений:
, поэтому можно записать связанную систему уравнений:
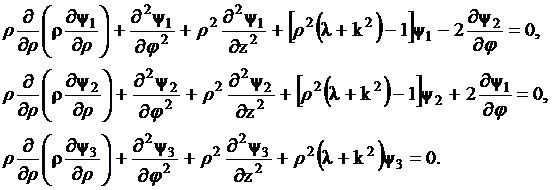 (3.3)
(3.3)
Граничные условия для электрического потенциала имеют вид:
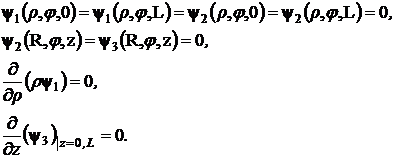 (3.4)
(3.4)
Требование однозначности ![]() , накладывает также условие периодичности всех
, накладывает также условие периодичности всех ![]() по
по ![]() .
.
Аналогично для магнитного потенциала имеем граничные условия:
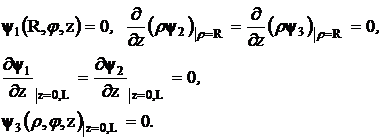 (3.5)
(3.5)
и условие периодичности по ![]() по
по ![]() .
.
Система уравнений (3.3) с граничными условиями (3.4) или (3.5) решается методом разделения переменных, в результате чего получаются три линейно-независимых вектор-решения. Каждое такое решение определено с точностью до произвольной постоянной. В результате для спектра в случае электрического потенциала получается:
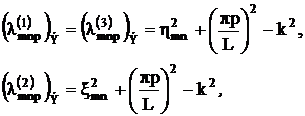 (3.6)
(3.6)
где индекс "Э" указывает на принадлежность собственных числе спектру электрического потенциала, m, n, р - целые числа, а коэффициенты ![]() и
и ![]() связаны с нулями
связаны с нулями ![]() „ и
„ и ![]() функций Бесселя
функций Бесселя ![]() и их производных
и их производных ![]() :
:
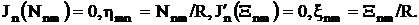 (3.7)
(3.7)
Три фундаментальных вектора-решения системы (3.3) с граничными условиями (3.4) для электрического потенциала имеют вид:
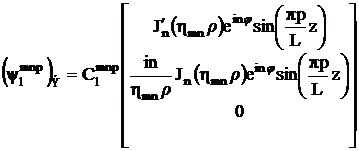 ,
,
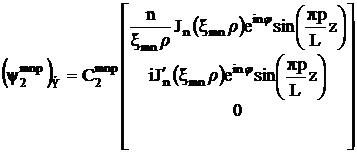 , (3.8)
, (3.8)
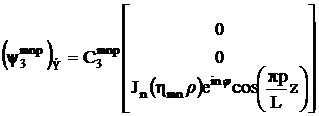 .
.
Здесь ![]() - нормирующие коэффициенты:
- нормирующие коэффициенты:
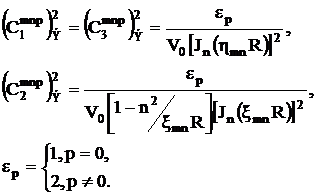 (3.9)
(3.9)
Для спектра в случае магнитного потенциала получается
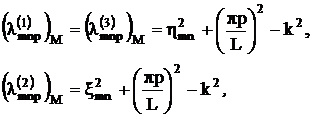 (3.10)
(3.10)
Можно заметить, что произошло простое изменение нумерации ветвей спектра по сравнению со случаем электрического потенциала.
Фундаментальные решения системы (3.3) с граничными условиями (3.5) для магнитного потенциала имеют вид:
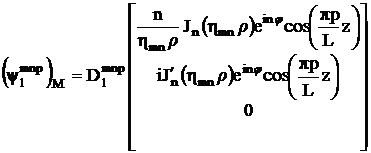 ,
,
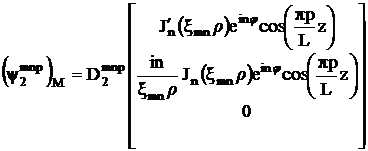 , (3.11)
, (3.11)
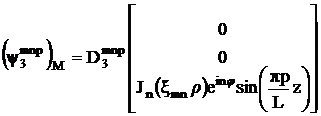 .
.
Нормирующие коэффициенты:
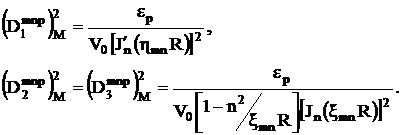 (3.12)
(3.12)
Чтобы не проводить суммирование по m и n от -∞ до +∞, удобно представить ![]() в виде:
в виде:
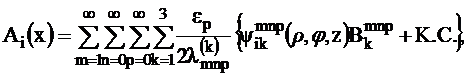 (3.13)
(3.13)
где К. С. означает комплексное сопряжение и амплитуды запишется в виде:
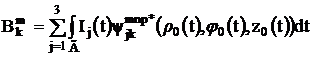 (3.14)
(3.14)
Здесь Г задается в цилиндрических координатах, а:
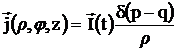 , (3.15)
, (3.15)
где р - точка, принадлежащая поверхности S', на которой заданы эквивалентные токи, а q - произвольная точка в объеме отсека.
Формулы (3.13), (3.14) справедливы как для электрического, так и для магнитного потенциалов.
Выпишем нормальные электрические и магнитные колебания ![]() и
и ![]() . Вклад в нормальные колебания дают электрические и магнитные токи, которые не связаны друг с другом. Поэтому естественно разбить
. Вклад в нормальные колебания дают электрические и магнитные токи, которые не связаны друг с другом. Поэтому естественно разбить ![]() и
и ![]() на две части, каждая из которых будет входить в разложение поля с разными коэффициентами, зависящими соответственно от электрических и магнитных токов.
на две части, каждая из которых будет входить в разложение поля с разными коэффициентами, зависящими соответственно от электрических и магнитных токов.
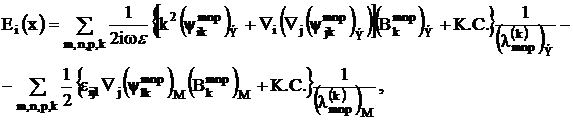 (3.16)
(3.16)
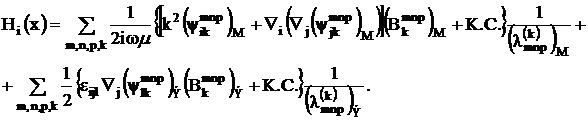 (3.17)
(3.17)
Естественно ввести следующие обозначения:
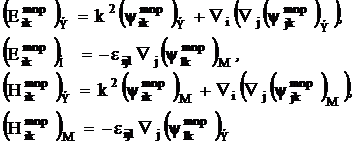 (3.18)
(3.18)
Явное вычисление этих величин дает следующий результат:
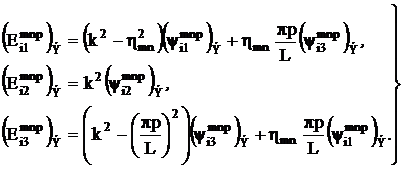 (3.19)
(3.19)
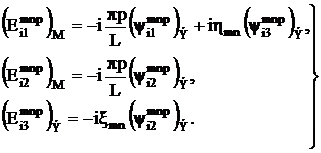 (3.20)
(3.20)
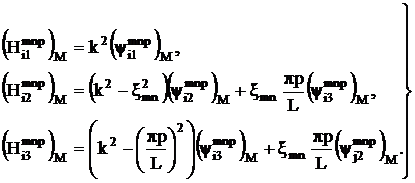 (3.21)
(3.21)
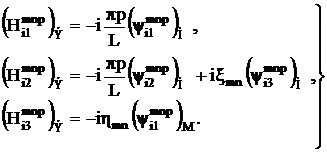 (3.22)
(3.22)
Выражения для напряженности полей можно теперь записать:
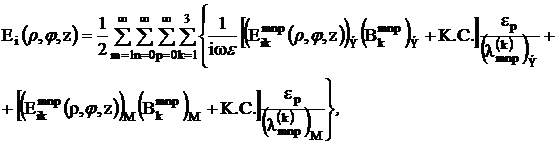 (3.16)
(3.16)
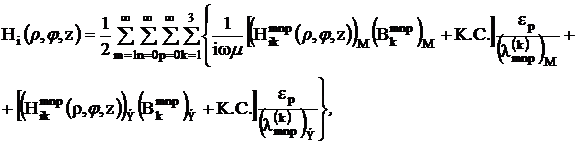 (3.17)
(3.17)
В знаменатель разложения полей (3.22)-(3.24) входят собственные числа (3.5), (3.9). При определенных частотах эти собственные числа могут обращаться в нуль, приводя к бесконечным амплитудам полей в цилиндре (резонанс). На самом деле амплитуды не достигают бесконечных значений из-за потерь на стенках резонатора. Учет таких потерь можно провести, введя малую добавку в частоту. Причем такая добавка существенна только в ![]() , а во всех остальных местах ее можно опустить. Положим:
, а во всех остальных местах ее можно опустить. Положим:
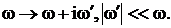 (3.25)
(3.25)
Мнимую часть ![]() можно выразить через добротность резонатора
можно выразить через добротность резонатора ![]() , тогда:
, тогда:
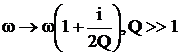 (3.26)
(3.26)
Теперь, если ![]() совпадает с одной из собственных частот резонатора
совпадает с одной из собственных частот резонатора ![]() , то некоторые
, то некоторые ![]() становятся чисто мнимыми. Это предотвращает бесконечный рост амплитуды поля.
становятся чисто мнимыми. Это предотвращает бесконечный рост амплитуды поля.
Для цилиндрического резонатора собственные частоты определяются выражениями:
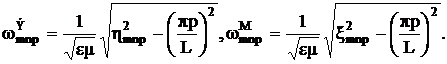 (3.27)
(3.27)
Итак, электромагнитная обстановка в приборном отсеке цилиндрической формы в месте расположения устройства ![]() на частоте
на частоте ![]() для некоторого штатного состояния определяется модулями
для некоторого штатного состояния определяется модулями 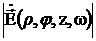 и
и 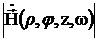 напряженностей электрического
напряженностей электрического ![]() и магнитного
и магнитного ![]() полей (3.23) и (3.24).
полей (3.23) и (3.24).

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 |




