Координационное расстояние рассчитывается по формуле:
![]() , (2.33)
, (2.33)
где: 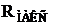 - радиус зоны вещания передатчика без учета помех;
- радиус зоны вещания передатчика без учета помех;
![]() - расстояние от границы зоны полезного передатчика до помехи.
- расстояние от границы зоны полезного передатчика до помехи.
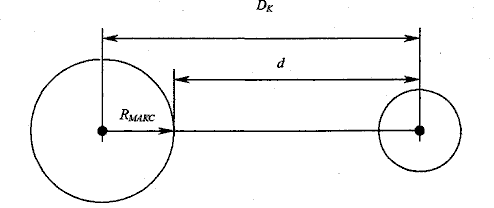
Рис.2.8. Определение координационного расстояния.
На границах зон рассматриваемых передатчиков должны выполняться условия качественного приема:
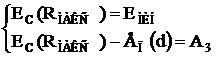 , (2.34)
, (2.34)
где: ![]() - напряженность поля сигнала на границе зоны вещания, дБ;
- напряженность поля сигнала на границе зоны вещания, дБ;
![]() - минимально-допустимая напряженность поля сигнала на границе зоны, при которой обеспечивается качественный прием на существующую массовую аппаратуру, дБ.
- минимально-допустимая напряженность поля сигнала на границе зоны, при которой обеспечивается качественный прием на существующую массовую аппаратуру, дБ.
Из выражения (2.34) получим выражение для определения максимального радиуса зоны вещания 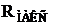 :
:
![]() , (2.35)
, (2.35)
где 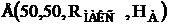 - напряженность поля сигнала на расстоянии
- напряженность поля сигнала на расстоянии ![]() от передатчика, определяется по кривым распространения, дБ.
от передатчика, определяется по кривым распространения, дБ.
Зная эффективную высоту подвеса антенны ![]() , и эффективную излучаемую мощность
, и эффективную излучаемую мощность ![]() , методом деления пополам можно найти такой радиус зоны вещания, что
, методом деления пополам можно найти такой радиус зоны вещания, что ![]() будет равна разности
будет равна разности ![]() с заданной степенью точности.
с заданной степенью точности.
Исходя из равенства (2.34) найдем значение d. Напряженность поля помехи:
![]() (2.36)
(2.36)
где: 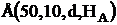 - напряженность поля помехи, создаваемая передатчиком с эффективной излучаемой мощностью 1 кВт, дБ;
- напряженность поля помехи, создаваемая передатчиком с эффективной излучаемой мощностью 1 кВт, дБ;
![]() - помехозащищенность приемной антенны, дБ.
- помехозащищенность приемной антенны, дБ.
Определяя единичную напряженность поля помехи, методом деления пополам можно найти d. При распределении частотных каналов в регулярной однородной сети ввиду идентичности параметров и помеховой обстановки всех передатчиков, достаточно определить координационное расстояние для одной пары. Для всех остальных подобных пар данное расстояние можно использовать в качестве показателя оптимальности частотных присвоении.
В реальной передающей сети станции размещены нерегулярно, параметры каждого передатчика индивидуальны и помехи, создаваемые друг другу, неравнозначны. Следовательно, необходимо исследовать условия работы обоих передатчиков и для каждого из них определить расстояние до помехи, при котором выполняются требования качественного приема. Рассмотрим два взаимно мешающих передатчика, технические параметры которых не одинаковы (см. рис.2.9).
Исходя из рис.2.9 для i-го передатчика минимально-допустимое расстояние до j-го должно быть ![]() . В свою очередь, чтобы обеспечить необходимое качество приема j-го передатчика, требуется расстояние от него до i-го
. В свою очередь, чтобы обеспечить необходимое качество приема j-го передатчика, требуется расстояние от него до i-го ![]() . Причём
. Причём ![]() . Координационным расстоянием
. Координационным расстоянием ![]() считается больше из этих двух расстояний:
считается больше из этих двух расстояний:
![]() (2.37)
(2.37)
Для оценки оптимальности данного частотного присвоения паре передатчиков необходимо определить их координационное расстояние и сравнить его с фактическим расстоянием между ними. Можно рассматривать следующую формальную конструкцию:
если 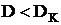 , то данное присвоение запрещено, в любом другом случае разрешено.
, то данное присвоение запрещено, в любом другом случае разрешено.
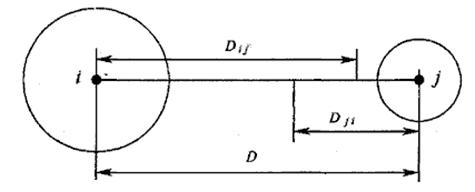
Рис. 2.9. Выбор координационного расстояния
Такая конструкция предполагает оптимизацию с точки зрения использования технических ресурсов станции. Но в случае ![]() формальное разделение частотного присвоения не оптимально с точки зрения использования частотного спектра.
формальное разделение частотного присвоения не оптимально с точки зрения использования частотного спектра.
Поэтому для оптимизации частотных присвоений предлагается ввести пределы, в которых допустимо отклонение рассматриваемого расстояния от координационного:
![]() (2.38)
(2.38)
Если D расположено в этом интервале, можно сказать, что данное присвоение частот является оптимальным. Точность этого критерия определяется тем, что его численные значения рассчитываются из условий качественного приема только в одной точке на границе зоны вещания передатчика. Однако недостатком координационного расстояния является то, что его оптимальное значение для каждой пары передатчиков - свое, интервал оптимальных присвоений заранее не определён в отличие от КВВ (коэффициента взаимного влияния). Плохо и то, что интервал оптимальных присвоений приходится задавать в долях оптимального (координационного) расстояния между станциями, а не в долях изменения потенциальных радиусов зон вещания.
Связь между этими параметрами не линейна, поэтому при незначительном отклонении фактического расстояния от координационного, нельзя утверждать, что фактический радиус будет отличаться от ![]() также незначительно.
также незначительно.
По сравнению с показателем “используемая напряженность поля” показатель “координационное расстояние” является более точным показателем эффективности, т. к. используемая напряженность поля оценивает только возможность данного частотного присвоения, в то время как координационное расстояние определяет оптимальность этого присвоения. Если недостаточно проанализировать взаимные помехи передатчиков только в одной точке на границах зон вещания, необходимо воспользоваться в качестве показателя оптимальности частотных присвоений предложенным коэффициентом использования передатчиков, т. к. он, в отличие от координационного расстояния, исследует влияние помехи на всю зону передатчика с любой заданной степенью точности - отсюда и его вычислительная сложность как минимум на порядок выше.
Коэффициент взаимного влияния. Для количественной оценки оптимальности частотного планирования и оптимизации технических параметров передающих сетей предлагается ввести новый показатель эффективности - коэффициент взаимного влияния (КВВ) - величина, количественно оценивающая взаимное влияние пары передатчиков. Этот коэффициент определяет, насколько изменяются радиусы зон вещания передающих станций относительно максимальных под воздействием взаимных помех. Предлагается определять КВВ по следующей формуле:
![]() , (2.39)
, (2.39)
где ![]() и
и ![]() - радиусы зон вещания i-го и j-го передатчиков по направлению друг к другу, км;
- радиусы зон вещания i-го и j-го передатчиков по направлению друг к другу, км;
![]() и
и ![]() - радиусы зон вещания i-го и j-го передатчиков в противоположных направлениях, км;
- радиусы зон вещания i-го и j-го передатчиков в противоположных направлениях, км;
![]() и
и ![]() - радиусы зон вещания i-го и j-го передатчиков при условии отсутствия помех
- радиусы зон вещания i-го и j-го передатчиков при условии отсутствия помех ![]() , км.
, км.
В однородной сети, где параметры всех передатчиков одинаковы, можно использовать в качестве критерия коэффициент, рассчитанный таким образом. Рассмотрим пару передающих станций в реальных условиях. Каждая из них обладает индивидуальными параметрами и соответственно помехи, создаваемые ими, различны. Если эти помехи соизмеримы, КВВ дает верную оценку взаимных влияний пары передатчиков.
Однако возможна ситуация, когда взаимно мешающие частотные каналы присваиваются передатчикам, резко различающимися по уровню создаваемых помех. Допустим i-й передатчик в силу своих технических возможностей охватывает вещанием гораздо большую зону, чем j-й (см. рис.2.10).
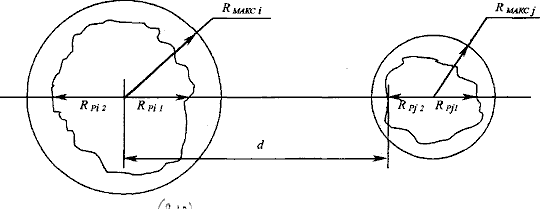
Рис.2.10. К расчету коэффициента влияния
Следовательно, радиусы зоны ![]() ,
, ![]() и
и 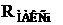 намного превысят соответствующие им
намного превысят соответствующие им ![]() ,
, ![]() и
и 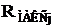 . Тогда при расчете КВВ (2.39) будет учтено только сокращение зоны мощного передатчика (i-го) под воздействием помехи от j-го, т. к. параметры зоны маломощного передатчика слабо влияют на результат вычислений по причине их малой величины. То есть при расчете КВВ по формуле (2.39) в данном случае будет учтено только влияние маломощной станции на мощную, а помехи, создаваемые мощным передатчиком не оцениваются. Из всего вышеизложенного следует, что КВВ, рассчитанный по (2.39), не рекомен-дуется использовать в качестве критерия оптимальности частотных присвоений в неоднородной сети. Поэтому был предложен другой вариант расчета коэффициента взаимного влияния пары передатчиков, который определяется из условия:
. Тогда при расчете КВВ (2.39) будет учтено только сокращение зоны мощного передатчика (i-го) под воздействием помехи от j-го, т. к. параметры зоны маломощного передатчика слабо влияют на результат вычислений по причине их малой величины. То есть при расчете КВВ по формуле (2.39) в данном случае будет учтено только влияние маломощной станции на мощную, а помехи, создаваемые мощным передатчиком не оцениваются. Из всего вышеизложенного следует, что КВВ, рассчитанный по (2.39), не рекомен-дуется использовать в качестве критерия оптимальности частотных присвоений в неоднородной сети. Поэтому был предложен другой вариант расчета коэффициента взаимного влияния пары передатчиков, который определяется из условия:
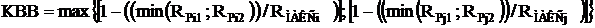 . (2.40)
. (2.40)
Таким образом, КВВ определяется только одним из условий качественного приема (2.34):
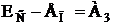 . (2.41)
. (2.41)
Этот коэффициент оценивает ситуацию, учитывая только взаимные помехи между двумя передатчиками. Положительные значения КВВ при ![]() указывают на недостаточное использование технических ресурсов передатчиков, при отрицательных значениях коэффициента
указывают на недостаточное использование технических ресурсов передатчиков, при отрицательных значениях коэффициента ![]() можно говорить о нерациональном использовании частотного спектра. Случай, когда КВВ=0, является наилучшим, т. к. при этом выполняются оба условия (2.34) качественного приема. Необходимо имперически определить интервал значений КВВ вокруг нуля, при которых частотные присвоения оптимальны и в смысле использования технических параметров передатчиков, и в смысле использования спектра.
можно говорить о нерациональном использовании частотного спектра. Случай, когда КВВ=0, является наилучшим, т. к. при этом выполняются оба условия (2.34) качественного приема. Необходимо имперически определить интервал значений КВВ вокруг нуля, при которых частотные присвоения оптимальны и в смысле использования технических параметров передатчиков, и в смысле использования спектра.
По сравнению с коэффициентом использования передатчика, КВВ гораздо проще с точки зрения расчетов, но когда требуется оценить взаимное влияние передатчиков на всю зону вещания, а не только в двух точках на границе этой зоны, необходимо пользоваться рассматриваемым ниже более точным показателем оптимальной частотных присвоений - коэффициентом использования передатчика. В свете вышесказанного можно заключить, что коэффициент взаимного влияния - весьма простой, эффективный и наглядный показатель, которым удобно пользоваться при оптимизации частотных присвоений.
Коэффициент использования передатчика. Предлагаемый коэффициент использования передатчика представляет собой отношение площади обслуживания данной станции в сети ![]() к площади обслуживания при отсутствии помех
к площади обслуживания при отсутствии помех 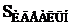 :
:
![]() (2.42)
(2.42)
Коэффициент использования передатчика является очень точным показателем эффективности, т. к. учитывает влияние помехи на всю зону вещания передатчика. Но вместе с тем он самый сложный для расчета, потому что нужно делать в несколько раз больше вычислений, чем, например, при расчете КВВ или координационного расстояния, когда считается изменение зоны обслуживания передатчика только в направлении на помеху. Кроме того, Q является хорошим критерием оптимизации частотных присвоении лишь тогда, когда он меньше единицы, т. е. когда помеха влияет на зону передатчика. В случае же, когда Q = L мы оцениваем эффективность присвоения только с точки зрения использования ресурсов передатчика, а оценить использование спектра мы не можем. Но, если так же как при расчете КВВ реальный радиус рассчитывать, пренебрегая граничным условием ![]() , т. е., если изменение Q считать не в пределах [0;1], а расширить границы диапазона
, т. е., если изменение Q считать не в пределах [0;1], а расширить границы диапазона ![]() , то оптимальность очередного текущего присвоения можно рассмотреть и по использованию технических ресурсов передатчика и по использованию спектра:
, то оптимальность очередного текущего присвоения можно рассмотреть и по использованию технических ресурсов передатчика и по использованию спектра:
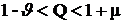 (2.43)
(2.43)
Коэффициент использования передатчика - парный показатель, т. е. Q рассчитывается для каждого из пары взаимно мешающих передатчиков, а эффективность присваиваемой частоты оценивается по меньшему коэффициенту.
Таким образом, с учетом предложенного расширения границ изменения Q, его можно использовать в качестве системного показателя оптимальности частотных присвоений передатчикам, находящимся на любом расстоянии друг от друга в любых передающих сетях, если необходима очень точная оценка и имеются достаточно большие ресурсы машинного времени.
Сравнение показателей эффективности позволило сделать вывод о том, что самым простым, т. е. требующим наименьших ресурсов машинного времени является используемая напряженность поля в точке установки передатчика ![]() . Но этот показатель наименее точный, т. к. раскрывает лишь качественную сторону частотных присвоений.
. Но этот показатель наименее точный, т. к. раскрывает лишь качественную сторону частотных присвоений.
Более точными показателями эффективности являются координационное расстояние ![]() , и предлагаемый коэффициент взаимного влияния. По времени расчета и по точности даваемой оценки КВВ и
, и предлагаемый коэффициент взаимного влияния. По времени расчета и по точности даваемой оценки КВВ и ![]() очень близки друг к другу. КВВ рассчитывается в относительных единицах.
очень близки друг к другу. КВВ рассчитывается в относительных единицах.
Наиболее точным при определении оптимальности присвоения частотных каналов в передающей сети вещания является предложенный коэффициент использования передатчика Q, потому что он рассчитывает влияние помехи на всю зону вешания. Вместе с тем расчет требует на порядок больше машинного времени. Более того, количественно оценивает ситуацию лишь для передатчиков, удаленных
на такое расстояние друг от друга, что 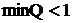 , если же
, если же ![]() , то оказывается, что оба данных передатчика могут работать в одном частотном канале, а сделать вывод об оптимальности использования спектра в этом случае не удается. Это можно сделать, используя КВВ.
, то оказывается, что оба данных передатчика могут работать в одном частотном канале, а сделать вывод об оптимальности использования спектра в этом случае не удается. Это можно сделать, используя КВВ.
Таким образом, анализ всех показателей эффективности оптимизации частотных присвоений позволил придти к следующему выводу: чтобы выбрать тот или иной показатель, необходимо правильно оценить обстановку (каким передатчикам присваиваются частоты - с одинаковыми параметрами или нет), задаться точностью, с которой нужно определить оптимальность присвоенного канала, учитывая имеющиеся ресурсы машинного времени, и времени, за которое нужно спланировать сеть.
Итак, показатели эффективности, используемая напряженность поля и координационное расстояние необходимо серьезно доработать, для того, чтобы его можно было использовать в практических целях, показатели КВВ и коэффициент использования передатчика можно рекомендовать к использованию при составлении частотных планов модернизации и развития передающих сетей.
2.4.2. Методы частотных присвоений в сетях радиовещания.
Линейные методы распределения каналов. В основу линейных методов планирования, наиболее широко описанных в литературе, положено понятие регулярной однородной сети радиовещания [12]. Для такой сети:
· параметры передатчиков и высота подвеса антенны идентичны;
· территориально ТВ станции размещены в вершинах равносторонних треугольников, образующих регулярную сетку;
· условия распространения во всех направлениях принимаются одинаковыми.
В этих условиях наивыгоднейшее соотношение радиуса полезной зоны, представляющей собой окружность, каждого передатчика со стороной трех полезных зон в центре элементарного треугольника. В этом случае площадь треугольника полностью обслужена. Как видно из рис.2.11 при указанных условиях
 (2.44)
(2.44)
где ![]() - модуль сети или расстояние между соседними передатчиками, км;
- модуль сети или расстояние между соседними передатчиками, км;
![]() - радиус полезной зоны передатчика при наличии помех, равный радиусу круга, площадь которого равна действительной площади зоны обслуживания данного передатчика, км.
- радиус полезной зоны передатчика при наличии помех, равный радиусу круга, площадь которого равна действительной площади зоны обслуживания данного передатчика, км.
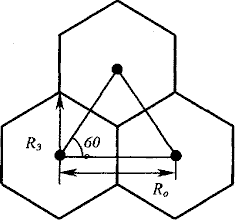
Рис.2.11. Пример регулярной схемы
В такой сети передатчики, работающие в совмещенных каналах, также располагаются на вершинах равносторонних прямоугольников со стороной D. Выбор величины D должен обеспечивать приемлемый уровень помех между этими передатчиками.
Два смежных равносторонних треугольника совмещенных каналов образуют ромб совмещенных каналов. Передатчики, установленные на вершинах элементарных треугольников внутри ромба, работают все на различных частотах.
Для составления частотных планов используется сетка, состоящая из равносторонних треугольников со стороной ![]() , оси координат которой параллельны сторонам треугольников, т. е. располагаются под углом 60° относительно друг друга (рис.2.12).
, оси координат которой параллельны сторонам треугольников, т. е. располагаются под углом 60° относительно друг друга (рис.2.12).
В каждой из вершин элементарного треугольника располагается передатчик. При расчетах территориального разноса и нумерации каналов используются координаты X и У, представляющие собой целые числа, при этом сторона элементарного треугольника ![]() = 1.
= 1.
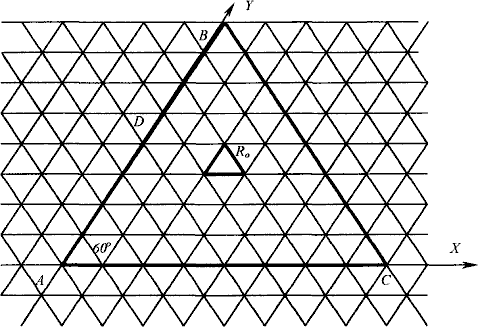
Рис.2.12. Пример регулярной сети
Рассмотрим несколько существующих методов частотного планирования в регулярной сети.
Метод триад. Триада - группа из трех целых положительных чисел ![]() , сумма которых равна числу распределяемых каналов (в пределах ромба совмещенных каналов), т. е.
, сумма которых равна числу распределяемых каналов (в пределах ромба совмещенных каналов), т. е.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 |




