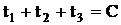Электронная совместимость радиоэлектронного оборудования (стр. 5 )

(2.45)

Число триады представляет собой разницу номеров каналов, присваиваемых передатчи­кам, расположенным в вершинах элементарных треугольников (рис.2.13).

На этом рисунке в качестве примера показан параллелограмм совмещенных каналов, ну­мерация каналов для С = 19 и триада t1 = 3, t2 = 2, t3 = 14. Для этой триады (при С = 19) паралле­лограмм совмещенных каналов является ромбом. Номера частотных каналов всех передатчиков, расположенных по оси Y или по прямой параллельно ей, отличаются друг от друга на t1, (при отчете сверху вниз); номера частотных каналов передатчиков, расположенных по оси X или по прямой, параллельной ей, отличаются друг от друга на t2. Номера отсчитываются по модулю С.

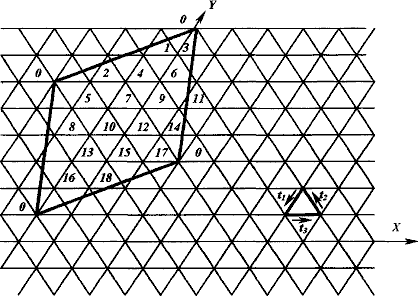
Рис. 2.13. Распределение каналов методом триад

Номер канала, расположенного вначале координат, равен 0. При выборе триад нужно руково­дствоваться следующим:

·  используются только те триады, которые содержат разные числа, а не их переста­новки;

·  не должны использоваться те триады, все числа которых имеют общий делитель с числом каналов С.

После того, как выбрана триада, для каждой из них строят параллелограмм совмещенных каналов. Выбирают ту триаду, при которой может быть получен ромб совмещенных каналов (или параллелограмм, наиболее близкий к ромбу). Этим обеспечивается наиболее равномерное распределение совмещенных каналов по всей территории. Определив территориальное распо­ложение передатчиков, работающих в совмещенных каналах, непосредственно по сетке, опре­деляются координаты остальных передатчиков, расположенных в вершинах элементарных тре­угольников, заполняющих площадь параллелограмма.

Метод относительных расстояний. Как и в методе триад, в данном случае используются косоугольная сетка из равносторон­них элементарных треугольников. На этой сетке строится ромб со сторонами X = С и Y = С, отло­женными по осям X и Y, в углах этого ромба размещаются передатчики. В основе этого метода лежит обязательное условие: совмещенные каналы должны располагаться в вершинах равно­сторонних треугольников (ромбов). При таком построении ромба совмещенных каналов число узловых точек равно С2, в то время как число размещенных каналов передатчиков внутри ром­ба равно С. Поэтому не в каждой узловой точке будет находиться передатчик.

Для того, чтобы найти координаты наивыгоднейших мест расположения остальных пере­датчиков, необходимо задаться соотношением Y = nХ, (где n - целое число) и при данном n для каждого значения X (от 1 до С) определить соответствующее значение Y. Величина n может ме­няться в пределах от 2 до С/2. При n ≥ С/2 варианты размещения каналов повторяются. Вели­чины n = 0 и n = 1 непригодны, т. к. при n = 0 все передатчики располагаются вдоль оси X, а при n = 1 - по диагонали ромба (т. к. X = Y).

Все варианты, полученные при различных значениях наносят на сетку и выбирают то значение, при котором передатчики внутри ромба совмещенных каналов располагаются в вершинах равно­сторонних треугольников, наиболее близких по форме к равносторонним.

Найдя наивыгоднейшее территориальное расположение передатчиков, определяют опти­мальное распределение номеров каналов, считая номер канала в начале координат равным 0.

Метод Хеада. Данный метод по существу является частным случаем метода триад, т. к. здесь рассматри­ваются лишь те случаи, когда передатчики совмещенных каналов расположены в вершинах ромбов, а внутри ромба все остальные передатчики в узлах сетки. В этом случае число каналов С выражается в виде:

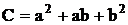, (2.46)

где а = X1 и b = Y1 - координаты ближайшего к началу координат совмещенного канала. Пре­образовав выражение (2.46), получим:

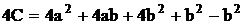, (2.47)

где величина b принимает значение чисел последовательного ряда (0,1,2,3,…,n).

Если извест­но С, то из (2.47) можно определить а и b. То есть при заданном С нужно подобрать число, квад­рат которого равен одному из значений: 4С, (4С - 3), (4С - 12), (4С - 27) и т. д. В зависимости от того, какое число является полным квадратом, определится b, которое может быть равно 0, 1, 2, и т. д. Зная b, легко определить а. Если до значения решение не получено, то при за­данном числе С нельзя получить ромбы совмещенных каналов. Поэтому применение этого ме­тода возможно только при определенных значениях С. Если же решение найдено, это значит, что положение ромба совмещенных каналов определено.

Далее необходимо распределить номера частотных каналов передатчикам, расположен­ным внутри ромба совмещенных каналов. В зависимости от соотношения величин а и b в дан­ном методе предложены различные формулы для определения номеров каналов.

1. а и b - взаимно простые числа. В этом случае номер частотного канала передатчика с координатами Xi и Yi определяются по формуле:

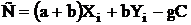, (2.48)

где g = 0, ± 1, ± 2 и т. д.

Так же как и в предыдущих методах номер канала определяются по модулю С. Вместо то­го, чтобы определять номер канала для всех значений Хi и Yi достаточно вычислить его с точки координаты Х = 0 и Y = 1, затем, двигаясь верх по оси Y надо прибавлять величину b к номеру канала предыдущего передатчика. Продвигаясь по линии, параллельной оси X, надо прибавлять (а + b) к номеру канала предыдущего передатчика, если он расположен справа от оси Y и вычи­тать (а + b) - если слева от нее.

2. а и b имеют общий делитель, больший единицы. Номер канала передатчика с координа­тами Хi, Yi вычисляется по формуле:

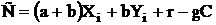, (2.49)

где r - остаток от деления на Y, на общий множитель h.

Сопоставление основных особенностей рассмотренных методов. Общим показателем для всех рассмотренных методов является линейное распределение местоположения передатчиков и номеров частотных каналов. Однако номера каналов, присваиваемых передатчикам, распределенных разными методами, при одних и тех же координатах могут не совпадать. Предпосылки, заложенные при определении территориального положения передатчиков в раз­ных методах не одинаковы.

В методе триад принято, что сеть состоит из равносторонних элементарных треугольни­ков, что касается формы параллелограмма совмещенных каналов, то она может быть любой и превращается в ромб лишь при определенном С и соответствующем выборе триады.

В методе относительных расстояний заложено расположение передатчиков совмещенных каналов в вершинах равносторонних треугольников, т. е. параллелограмм совмещенных каналов является ромбом. Причем передатчики внутри ромба располагаются не в каждом узле решетки. В этом методе не при любом значении получаются равносторонние треугольники.

В методе Хеада рассматриваются лишь те случаи, когда, как передатчики совмещенных каналов, так и все остальные передатчики сети, расположены в вершинах равносторонних эле­ментарных треугольников. Поэтому его применение ограничено определенными значениями С.

Таким образом, метод триад является наиболее универсальным из рассматриваемых. Трудностью его применения является необходимость перебора всех возможных триад для на­хождения оптимальной, особенно в случаях больших значений С, когда число триад велико.

Из приведенных выше соображений можно сделать следующие выводы:

1.  Метод Хеада можно применять во всех случаях, когда при заданном С можно получить ромбы совмещенных каналов, а внутри ромба передатчики располагаются в узлах сетки.

2.  Метод относительных расстояний необходимо применять в тех случаях, когда необхо­димо сохранить расположение передатчиков совмещенного канала в вершинах ромба и допус­тимо размещение остальных не во всех узлах сетки.

3.  Метод триад является наиболее универсальным, так как позволяет получить размеще­ние передатчиков совмещенного канала не только в вершинах ромба, но и параллелограмма.

4.  Данные методы весьма эффективны, если планирование производится на относительно
равнинной местности и существующая сеть не накладывает действенных ограничений (либо мала, либо вообще не существует), а так же, если распределяются каналы неосвоенного диапа­зона.

5.  Использование рассмотренных методов частотного планирования в регулярной сети по­лезно при моделировании сети телевизионного и звукового радиовещания и при оценке влия­ния ее технических параметров, расстояние между станциями на число используемых частот­ных каналов и технико-экономические показатели.

6.  Ограниченность применения линейных методов частотного планирования заключается в идеализации территориального размещения станций, условий распространения и однородно­сти параметров.

Универсальная модель однородной сети. Для решения задач оптимального частотного планирования широко используется теория регулярных решеток [46], однако, использование рассмотренных мето­дов весьма затруднительно для синтеза таких сетей на ЭВМ.

Поэтому, в качестве модели принимаем однородную сеть регулярной структуры, в кото­рой каждая передающая станция находится в равных условиях по расположению и уровню помех. Сплошное обслуживание территории обеспечивается при мозаичном покрытии, когда за зону обслуживания передающей станции принимается равносторонний шестиугольник с цен­тром в точке ее расположения. Поскольку реальная зона обслуживания передающей станции является кругом, то использование в модели зоны шестиугольника обеспечивает минимальное перекрытие зон соседних передающих станций, в отличие от зоны в виде квадрата и треуголь­ника (см. рис. 2.14).

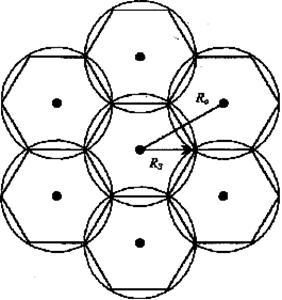
Рис.2.14. Сотовая структура однородной сети

В рассматриваемой сети расстояние между всеми соседними станциями одинаково - обо­значим его через и назовем модулем сети. Если за зону вещания передающей станции при­нять круг, в который вписан шестиугольник, то ее радиус будет связан с модулем сети со­отношением:

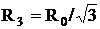. (2.50)

При синтезе модели однородной сети радиовещания необходимо определить расположе­ние передатчиков, работающих в совмещенных каналах, для чего предлагается использовать универсальную модель однородной сети (рис.2.15). В этой модели сети передающие станции, по­мещенные в центры шестиугольников с одинаковыми номерами, образуют ромб совмещенных каналов. Поскольку расстояние между передатчиками, работающими в совмещенных каналах одинаково, его нетрудно определить из геометрии сети. Так, если передатчики, работающие в совмещенных каналах, размещены в центрах шестиугольников под номером 1, то расстояние между ними равно модулю сети или, если представлять его в модулях сети:

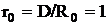. (2.51)

Расстояние между передатчиками, размещенными в центрах шестиугольников под номе­ром 2, можно определить из треугольника АВС (рис.2.16,а).

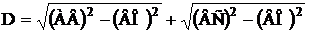. (2.52)

Учитывая, что , , 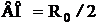из (2.52) получим:

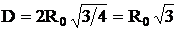. (2.53)

Расстояние между передатчиками, размещенными в центрах шестиугольника под номером 3, можно определить из рис.2.15, очевидно, что оно равно:

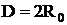. (2.54)

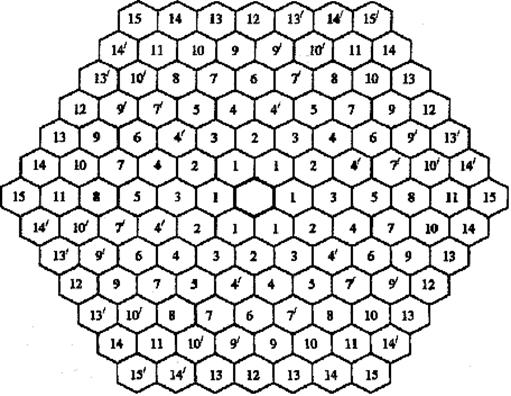
Рис.2.15. Определение расстояний до передатчиков, работающих в совмещенных каналах

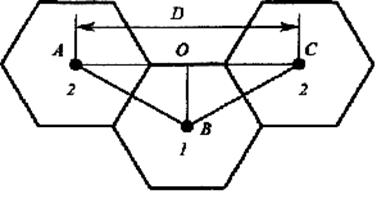
а

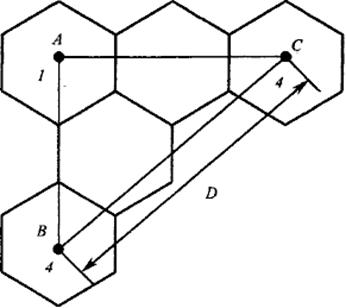
б

Рис.2.16. Определение расстояний в универсальной

модели однородной сети

Расстояние между передатчиками, размещенными в центрах шестиугольников под номе­ром 4, определим из рис.2.16,б, из которого следует, что , , тогда с учетом (2.52) можно записать:

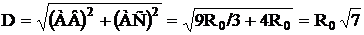. (2.55)

Аналогичным образом определяются расстояния между передатчиками, работающими в совмещенных каналах для других сетей 4, 5, и т. д. Штрихами 4/ , 7/ и т. д. обозначены сети, которые имеют одинаковое расстояние D с сетями 4, 7 и т. д., но другое расположение передат­чиков.

В центральный выделенный элемент, согласно проведенным расчетам, необходимо поме­щать номер рассматриваемой сети из табл. 2.3. Зная для различных сетей расстояние D между передатчиками, работающими в совмещенных каналах, определим число частотных каналов, необходимое для организации этих сетей. В однократной сети для сплошного покрытия заданной территории однопрограммным радиовещанием необходимое число частот­ных каналов определяется соотношением:

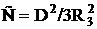. (2.56)

Таблица 2.1.

Номера сетей в универсальной модели однородной сети

Используя соотношения (2.50, 2.52) и данные табл. 2.3, можно определить значение С, когда передатчики, работающие в совмещенных каналах, размещаются в вершинах ромбов:

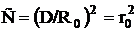. (2.57)

Таким образом, в предложенной универсальной модели однородной сети ее относитель­ный модуль r0 однозначно определяет количество необходимых частотных каналов.

Полученная в предложенной универсальной модели однородной сети взаимосвязь между значениями С и r0 (2.57) позволяет при заданном числе каналов синтезировать структуру однородной сети или же при заданной структуре сети определить необходимое число частотных каналов для обеспечения сплошного покрытия территории радиовещанием.

Использование теории графов для решения задачи распределения частотных присвоений. Основные понятия теории графов. Геометрический граф есть рисунок на плоскости, со­стоящий из вершин и ребер, соединяющих определенные пары этих вершин (рис.2.17). Алгеб­раический граф с множеством вершин V и множеством ребер Е YxY из декартово­го квадрата YxY, то есть:

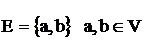, (2.58)

указывающее на то, что вершины а и b считаются соединенными ребром (а, b).

Если:

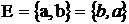, (2.59)

то ребро не ориентировано, оно принадлежит вершинам а и b. В примере на рис.2.17 ребро Еаb принадлежит вершинам а и b и т. д.

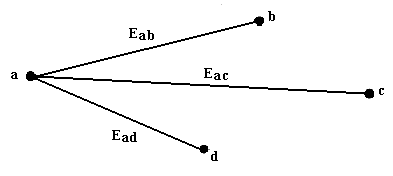
Рис.2.17. Пример графиков

Граф называется конечным, если число ребер конечно. Обычно число вершин в таком графе конечно. Если число ребер, принадлежащих одной вершине, обозначить S(а), то это число будет называться степенью графа в вершине а.

Каждое ребро Е графа G можно представить в виде элементарной квадратной матрицы М(G), рис.2.18. Элемент с координатами (а, b) может принимать значение 1 или 0 в зависимости от того существует или нет в графе G соответствующее ребро. Таким образом, мы получили матрицу смежности вершин М(G), которая полностью описывает граф.

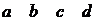
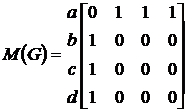
Рис. 2.18. Матрица смежности графа

Неориентированным графам соответствуют симметричные матрицы смежности. На рис. 11 приведена матрица смежности для графа, изображенного на рис.2.17.

Предположим, что G есть неориентированный граф с однократными ребрами без петель (т. е. без ребер, имеющих начало и конец в одной вершине). Тогда граф G называется k - рас­крашиваемым, если существует такое разбиение множества его вершин на k непересекающихся классов С1, С2, ..., Сk:

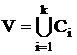, (2.60)

что вершины в каждом классе независимы, т. е ребра в графе соединят вершины из разных клас­сов. Наименьшее число классов в возможной раскраске называется хроматическим числом гра­фа G и обозначается:

. (2.61)

Предположим, что в нашем распоряжении имеется фиксированное число F цветов для со­поставления их вершинам графа G с множеством вершин V, тогда задача распределения данных цветов между вершинами графа G называется задачей о вершинной раскраске графа.

Существуют как точные, так и эвристические (приближенные) алгоритмы вершинной рас­краски графа. Точные алгоритмы гарантируют нахождение оптимальной раскраски и истинного значения хроматического числа для графа с малым числом вершин. Эвристические алгоритмы позволяют находить хорошие приближения для хроматического числа графа лишь в тех случа­ях, когда граф принадлежит лишь некоторым специальным классам. Однако для таких алго­ритмов часто отсутствуют доказательства того, насколько полученное хроматическое число от­личается от истинного.

Переходя конкретно к графу передающей сети ТВ и звукового радиовещания, можно ска­зать:

1.  Вершинами графа являются пункты установки передающих станций.

2.  Ребрами соединяются те передатчики, которые создают помехи приему в соответ­ствующей зоне обслуживания друг друга.

3.  Поскольку распространение радиоволн одинаково в обоих направлениях, то ребра являются неориентированными, однократными и без петель.

Таким образом, граф передающей сети радиовещания является конечным, неориентиро­ванным, с однократными ребрами и без петель. Отличительной особенностью геометрического графа передающей сети радиовещания является то, что он обладает дисковостъю, если сущест­вует такая константа R, что для любой его вершины 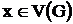множество смежных вершин ле­жат в круге радиуса R. Это объясняется тем, что каждый передатчик создает помехи только на расстоянии не больше координационного, поэтому для каждой вершины можно выделить об­ласть в виде круга с центром в ней самой, которая ограничивает совокупность смежных с дан­ной вершин.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9