Вероятностное прогнозирование ресурса нефтегазового оборудования при эксплуатации в сероводородсодержащих средах (стр. 4 )

Результаты приведенного выше и других анализов показывают, что величина D может изменяться от 50 до 200 % и выше. При этом D принимает большие значения при: t>tн; t< tн/(5¸10)); больших значениях коэффициентов вариаций параметров состояния и ресурса; малых значениях скорости накопления повреждений.

По результатам выполненных исследований были разработаны и апробированы на реальном оборудовании методические подходы, алгоритмы, зависимости, компьютерные программы обработки результатов измерения и оценки показателей вариаций значений и накоплен значительный банк данных о показателях вариаций значений критериев оценки технического состояния, параметров эксплуатационного нагружения и кинетики повреждаемости, наработки и значений прогнозируемого ресурса. Результаты исследований показывают, что значения параметров и критериев прогнозируемого ресурса оборудования имеют исходные и накапливаемые совместные вариации значений.

В четвертой главе представлены результаты обоснования и разработок моделей, критериев, алгоритма и методов прогнозирования ресурса оборудования по критериям допустимых вероятности и риска отказа.

Исследованиями установлено, что источниками снижения достоверности прогнозирования ресурса являются: вариации значений параметров состояния и ресурса; недостаточные объем и достоверность документируемой информации; недостаточный состав (набор) применяемых методов диагностики, оценок несущей способности и ресурса; ограниченный или недостаточный объем выборочного контроля. Основываясь на результатах выполненных исследований разработан алгоритм (рис. 3) прогнозирования ресурса, в пределах которого обеспечиваются допустимые вероятность и риск отказа.

Рисунок 3 – Алгоритм прогнозирования ресурса.

Методические основы прогнозирования ресурса базируются на последовательном применении элементов факторного анализа, матричных вычислений и вероятностно-статистического анализа с использованием ЭВМ, компьютерных программ математического, статистического анализа и собственных программных разработок.

В соответствии с алгоритмом рис. 3 обоснован и разработан метод определения показателей вариаций параметров состояния и ресурса. Метод основывается на определении перечня, выборок значений, статистическом анализе выборок и расчетах показателей вариации значений параметров состояния и ресурса. Перечень этих параметров определяется на основе данных о параметрах, входящих в модель прогнозирования ресурса, например зависимости (1), путем анализа результатов диагностического обследования. Выборки значений параметров составляются по данным диагностики, натурных и лабораторных исследований, стендовых испытаний, а также на основе сбора и анализа проектной, монтажной, эксплуатационной, ремонтной и документации. Для определения выборочных показателей вариации параметров - N; pmax; pmin; r; m; s, r - разработаны алгоритмы и компьютерные программы для их расчета на ЭВМ по известным зависимостям математической статистики. При отсутствии или недостатке данных, для определения показателей вариации параметров состояния и ресурса используется накопленный банк данных, например данные табл. 2-7. При отсутствии накопленных данных показатели вариаций параметров оцениваются на основе установленных эмпирических зависимостей (2)-(4) и при необходимости уточняются по результатам дополнительных измерений.

По результатам выполненных исследований разработана вариационная модель (В-модель) прогнозирования ресурса (рис. 4). В отличие от ДВ-модели (рис. 2 а) В-модель учитывает информацию о совместных вариациях входящих в нее параметров состояния и ресурса: tИ - исходной, ti - промежуточной, tн - текущей наработки; h0 - исходных, hi - промежуточных и hн - текущих параметров состояния; [h]0 - исходных, [h]i - промежуточных и [h]н - текущих критериев оценки состояния; параметров временных закономерностей - h(t) и [h](t) изменения параметров и критериев оценки состояния.

Было установлено, что совместные вариации параметров состояния и ресурса приводят к вариации значений t (рис. 5, заштрихованная область точек пересечения зависимостей h(t) и [h](t)), которые приводят к накоплению вероятности отказа - VLF. С использованием разработанной В-модели с учетом совместных вариаций параметров состояния и ресурса выполняется оценка значений допустимого (tv) ресурса (рис. 5), т. е. ресурса исчисляемого с момента текущей наработки tн, в период которого вероятность отказа будет не более допустимой - VLF£[V]LF.

Исследованиями было установлено, что каждая из n выборок значений параметров состояния и ресурса - переменных В-модели (рис. 5) - включает в себя определенное число - N контролируемых значений. Поэтому метод построения В-модели прогнозирования ресурса основывается на представлении исходной модели прогнозирования ресурса, например зависимостей (1), в виде аналитической функциональной зависимости ресурса от числовых выборок входящих в нее параметров. Аналитическая В-модель прогнозирования ресурса имеет вид:

(5)

где: p1, p2, …, pj - выборки случайных значений j-х переменных;
pj=pj1, pj2,…, pji – выборка значений j-й переменной; i – порядковый номер значения j-й переменной в выборке (i=1, 2, …, Nj); Nj - количество значений j-й переменной в выборке pj; ti – выборка значений прогнозируемого ресурса - t.

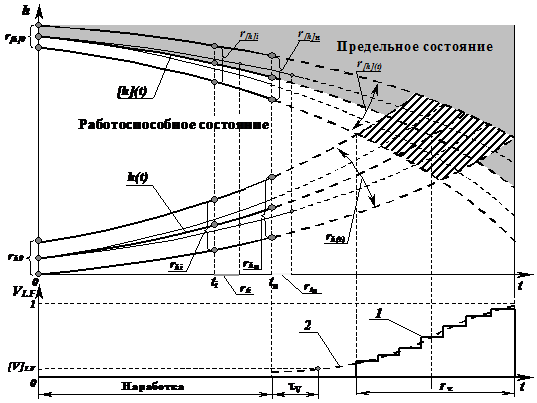
Рисунок 4 – В - модель прогнозирования ресурса: 1 и 2 – эмпирическая и теоретическая функции вероятностей отказа - V LF(t); r - размах вариаций параметров состояния и ресурса и t

По результатам выполненных исследований было установлено, что для различных переменных, входящих в В-модель (5), вариации их значений в различной степени влияют на достоверность прогнозирования ресурса. Причем из набора переменных В-модели для части переменных вариации их значений оказывают определяющее влияние на достоверность прогнозирования ресурса, а для другой части пренебрежимо малое и информацией о вариации этой части переменных при прогнозировании ресурса можно пренебречь. Для этого разработан метод факторного анализа параметров состояния и ресурса. По результатам анализа выявляются такие параметры состояния и ресурса, которые имеют определяющее влияние на достоверность прогнозирования ресурса. Для его реализации был разработан и применен методический подход на основе факторного анализа. Задача факторного анализа состоит в том, чтобы перейти от начальной системы большого числа переменных p1, p2, …, pj к меньшему числу переменных p1, p2, …, pk, k<j, изменение которых в значительной мере определяет изменение прогнозируемого ресурса - t по отношению к другим. Решение этой задачи выполняется по методике множественного регрессионного анализа. Для этого зависимость для ti записывается в следующем виде:

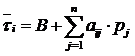, i=1, 2,…, N (6)

где: – условное среднее значение зависимой величины ti, соответствующее заданным значениям независимых переменных pj; В – неслучайная составляющая; aij – факторная «нагрузка»; j – количество факторов, т. е. переменных.

Решение задачи факторного анализа состоит в нахождении значений В и aij зависимости (6). Для этого строится матрица (Мр) независимых переменных pj размерностью j´N и матрица-столбец (Мt) зависимых значений ti. Каждый столбец матрицы Мр представляет собой N значений j-й независимой переменной pj. Матрица Мt представляет собой столбец значений ti (i=1, 2,…, N), где каждое ti рассчитывается с учетом соответствующих заданных значений pji по зависимостям прогнозируемого ресурса, которые строятся при диагностическом обследовании, например зависимостям (1).

Для построения матрицы Мр используются фактические выборочные данные pj. В случае отсутствия этих данных используются данные о статистических законах распределения этих выборок. Кроме этого было экспериментально доказано, что при отсутствии данных о законах распределения для построения матрицы Мр могут использоваться интегральное соотношение F(pj) нормального закона распределения и показателей вариации параметров состояния и ресурса –mj и sj, накопленные и содержащиеся в базе данных о показателях вариаций, например табл. 2-5, 7. Либо могут использоваться значения mj и sj, установленные по эмпирическим зависимостям (2), (3), (4). В этом случае, генерируя значения F(pj) от 0,01, до 0,99 с шагом 0,98/(N-1) и решая F(pj) относительно pj, получается j-й столбец матрицы Мр, содержащий N значений переменной pji.

Затем на матрицах Мt и Мр выполняется корреляционный, факторный анализ, вычисляются коэффициент (Rk) множественной корреляции, абсолютная (dk) ошибка, коэффициенты (aj) множественной регрессии и строится линейная регрессионная зависимость в натуральном масштабе вида:

, (7)

Поскольку число переменных (параметров состояния и ресурса) в зависимостях для прогнозирования ресурса, например зависимостях (1), как правило, не менее 6, реализация процедур многомерного факторного анализа возможна только с применением ЭВМ. Для реализации факторного анализа и построения выражения (7) был разработан специальный алгоритм с использованием пакета компьютерных программ статистического анализа.

Для оценки влияния изменения переменных pj на изменение t определяются стандартизованные коэффициенты (bj) множественной регрессии и выражение (7) представляется в стандартизованном масштабе:

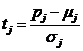; (8)

Было экспериментально доказано, что bj является критерием оценки влияния вариации переменных В-модели на достоверность прогнозирования ресурса. Установлено, что те переменные зависимости (7), у которых bj на порядок менее максимального bj, оказывают пренебрежимо малое влияние на изменение t, и информацией о вариации значений таких переменных в В-модели (5) можно пренебречь. Дальнейший расчет ресурса выполняется с учетом совместных вариаций только варьируемых переменных (wk), оказывающих определяющее влияние на достоверность прогнозирования ресурса. Переменные wk обозначаются в виде выборок значений – wk= w1, w2,…, wk; где: k=1, 2, …, nk - количество варьируемых переменных; wk= wk1, wk2,…, wki - выборка значений k-й переменной; i – порядковый номер значения k-й переменной в выборке (i=1, 2, …, Nk); Nk- количество значений k-й переменной. Состав этих переменных определяется путем исключения из состава переменных В-модели (5) тех переменных, информацией о вариации которых можно пренебречь.

После определения варьируемых переменных выполняется повторный факторный анализ, и строятся вторичные регрессионные зависимости в натуральном масштабе вида (7) и в стандартизованном масштабе вида (8), которые учитывают изменение значений ресурса - t от изменения варьируемых переменных (параметров состояния и ресурса) - wk:

, (9)

; (10)

Для построения зависимостей (9) и (10) строится матрица (Мw) переменных wk. Для этого из матрицы Мр исключаются те столбцы, которые не соответствуют wk, а матрица Мt остается прежней. Затем на матрицах Мt и Мw выполняется повторный факторный анализ, вычисляются значения коэффициентов - Bw и awk, а также коэффициент множественной корреляции - Rw и ошибка - dw множественной регрессии по которым оценивается адекватность зависимостей (9) и (10).

В соответствии с алгоритмом (рис. 3) разработан метод расчета ресурса при совместных вариациях параметров состояния и ресурса. Метод основывается на вычислении значений выборки t по зависимости (9), с использованием информации о вариациях и с учетом совместных вариаций значений варьируемых переменных - wk. Было экспериментально доказано, что выражение вида (9) в сравнении с применяемыми моделями прогнозирования ресурса, например (1), наилучшим образом подходит для вычислений t с учетом совместных вариаций wk поскольку, в сравнении с применяемыми моделями прогноза ресурса, в (9) отсутствуют операции взаимного деления и умножения сумм и разностей варьируемых переменных wk. Поэтому при учете совместных вариаций wk использование (9) не приводит: к неопределенности при делении на 0; к большим значениям t при знаменателях дроби близких к 0; положительным значениям t при перемножении и делении отрицательных величин. Выборка значений t с учетом совместных вариаций wk представляет собой линейную матрицу (столбец или строку) (tz= t1, t2,…,tz, z=1, 2, …, Nt) случайных величин, где каждое значение матрицы является решением выражения (9) при всех возможных сочетаниях значений wk по выражению:

i1=1, 2, …, N1; i2=1, 2, …, N2; …; ik=1, 2, …, Nk;

, (11)

Исследованиями установлено, что число варьируемых переменных - wk в зависимости (9) не менее четырех - k³4. Для исполнения нормативных требований и достоверного прогноза ресурса число значений переменных wk не менее десяти - Nk³ 10. В этом случае число (Nt = N1´N2´…´Nk) значений tz в матрице (11) ³ 104. Поэтому для вычисления tz был разработан специальный алгоритм и программа расчета tz на ЭВМ с применением процедур матричных вычислений.

Установлено, что прогнозирование ресурса должно основываться на оценке величины допустимого ресурса - tv, в пределах которого обеспечиваются допустимые вероятность - [V]LF и риск - [R]LF отказа. В соответствии с алгоритмом прогнозирования ресурса (рис. 3) по результатам исследований разработан метод определения допустимой вероятности отказа. Для обеспечения допустимого риска отказа - [R]LF оборудования в период продлеваемого ресурса разработан и использован подход, основанный на значениях допустимой вероятности отказа - [V]LF в зависимости от уровня (ULFi) тяжести последствий отказа. На основе анализа нормативных требований ГОСТ Р 51901.1–2002, РД 03–418-01 были обоснованы четыре уровня ULFi и критерии оценки ULFi: ULF1 – пренебрежимо малая тяжесть последствий, т. е. возникновение отказа не влияет на остановку производства и загрязнение окружающей среды; ULF2 (ULF3) - некритическая (критическая) тяжесть последствий, когда возникновение отказа не угрожает (угрожает) жизни людей, не приводит (приводит) к существенному ущербу имуществу и окружающей среде; ULF4 - катастрофическая тяжесть последствий, когда возникновение отказа приводит к гибели людей, существенному ущербу имуществу, невосполнимому ущербу окружающей среде. В соответствии с нормативными требованиями значения [V]LF для определенных ULFi характеризуются верхней и нижней границей значений. Для учета их в расчете ресурса были обоснованы уровни допустимого риска отказа - [R]LF: RHLF - высокий; RMLF – средний; RLLF – низкий. Это такие уровни [R]LF, при которых фактическая VLF соответствует верхней границе, середине диапазона и нижней границе диапазона значений [V]LF соответственно.

Разработанный в соответствии с алгоритмом прогнозирования ресурса (рис. 3) метод расчета допустимого ресурса - tv основывается на статистическом анализе выборки tz и построении эмпирического интегрального закона распределения вероятностей расчетных значений ресурса выборки tz. Этому закону распределения соответствует эмпирическая () функция вероятностей отказа на период прогнозируемого ресурса. Для полученной эмпирической функции определяется значение вероятности (Vmin), которое соответствует минимальному (tmin) значению, принадлежащему выборке tz. В зависимости от соотношения значений [V]LF и Vmin значения допустимого ресурса - tv, соответствующего периоду эксплуатации с вероятностью отказа VLF£[V]LF, вычисляются в следующем порядке. При [V]LF ³ Vmin tv вычисляется по функции - , полученной интерполяцией эмпирических значений . При
[V]LF < Vmin tv вычисляется по функции , полученной аппроксимацией эмпирических значений , а затем экстраполяцией их за пределы интервала . Результатами численных экспериментов было установлено, что наилучшая аппроксимация и экстраполяция эмпирических значений достигается путем аппроксимации вначале значений логарифма - 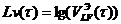полиноминальной моделью вида со значениями степени полинома n= 3¸5, а затем описания зависимостью вида - .

Значения tv вычисляются с учетом объема (e) выборочного контроля при диагностике, определяемого отношением площади контролируемой поверхности к общей площади металла элемента оборудования, путем решения уравнений:

. (12)

На основе выполненных численных экспериментов было доказано, что поскольку при [V]LF ³ Vmin используется функция , полученная интерполяцией , соответствующих эмпирическим значениям t, находящимся внутри выборки расчетных значений tz, значения наилучшим образом соответствуют фактической VLF. В этом случае оценка значений tv по имеет высшую достоверность. Кроме этого значения wk фактически являются экспериментальными данными, полученными на основе экспериментальных и теоретических исследований вариаций параметров состояния и ресурса. Поэтому значения tz также представляют собой массив экспериментальных данных, полученных при всех возможных сочетаниях экспериментальных значений этих параметров. Это способствует тому, что , полученная на таком количестве экспериментальных выборочных данных tz, стремится к предельному распределению выборки tz. При этом достоверность оценки tv является наилучшей, особенно в области малых (10-4 – 10-6) значений [V]LF.

Для статистического анализа выборки tz, построения функций
, , , решения уравнений (12) и вычисления tv были разработаны специальные алгоритмы и программы расчета на ЭВМ с применением сертифицированных пакетов программ и использованием их стандартных функций статистического анализа и обработки экспериментальных данных.

Исследованиями установлено, что по мере увеличения разницы между [V]LF и Vmin достоверность оценки допустимого ресурса - tv снижается. В соответствии с алгоритмом прогнозирования ресурса (рис. 3) по результатам исследований обоснован и разработан метод оценки уровней достоверности прогнозирования ресурса. Для оценки достоверности были обоснованы критерий (СV), уровни (DI) достоверности прогнозирования ресурса и разработана модель оценки уровней DI по критерию СV (рис. 5).

По результатам исследований теоретически обосновано и экспериментально подтверждено, что поскольку достоверность прогноза tv зависит от отношения величин промежутка, на котором выполняется наблюдение, т. е. , и промежутка, на который разрабатывается прогноз, т. е. от Vmin до [V]LF, то достоверность прогноза tv можно оценить критерием достоверности прогнозирования ресурса - СV, определяемым отношением СV= [V]LF/Vmin. Экспериментально установлено, что для прогнозирования tv промежуток VLF, на который разрабатывается прогноз, не должен быть больше чем на один порядок промежутка, на котором выполняется наблюдение. В зависимости от значений СV были обоснованы градации уровней достоверности прогнозирования ресурса: DIH – высокий, DIM - средний, DIL - низкий. Метод оценки достоверности основывается на вычислении СV и оценке уровня – DI с использованием модели оценки уровней достоверности прогнозирования ресурса (рис. 5).

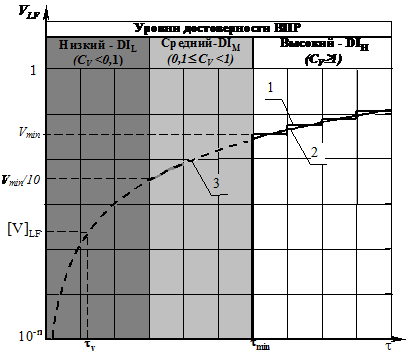
Рисунок 5 – Модель оценки уровней достоверности прогнозирования ресурса: 1 – ; 2 – ; 3 –

На основе анализа результатов выполненных исследований установлены три градации уровней (DM) достоверности методов диагностики параметров состояния: DMH – высокий; DMM - средний; DMND - достоверность отсутствует. И выполнена классификация методов по уровням достоверности диагностики DM. К DMH отнесены методы, позволяющие обеспечить диагностику параметров с погрешностью, не превышающей погрешность метода и применяемого средства измерения (прибора). К DMM отнесены методы, позволяющие обеспечить диагностику с погрешностью не более 30% и/или идентификацию повреждений (тип, размеры, форма) с погрешностью не выше 10 %. К DMND отнесены методы, которые не позволяют определять и не могут быть применены для диагностики соответствующих параметров состояния. Установлено, что применение двух и более методов, имеющих средний уровень - DMM, позволяют диагностировать параметры состояния с высоким уровнем достоверности - DMH.

Разработанный в соответствии с алгоритмом (рис. 3) метод оценки уровней достоверности диагностики параметров состояния основывается на анализе данных о применяемых методах диагностики и оценке уровней достоверности диагностики этих параметров – DM с использованием разработанной классификации методов по уровням DM. Для этого были разработаны алгоритм и компьютерная программа оценки уровней DM, когда задается набор параметров и информация о примененных методах диагностики и в соответствии с выполненной классификацией автоматически определяется уровень достоверности диагностики – DM.

Результатами численных экспериментов было установлено, что значение Vmin, соответствующее tmin выборки значений ресурса tz зависит от характера эмпирической функции и от числа значений Nt в выборке tz. На основе полученных экспериментальных данных теоретически обосновано и подтверждено экспериментально, что решением обратной задачи оценки достоверности прогнозирования ресурса можно определить требуемое минимальное число значений в выборке tz, которое при требуемом значении допустимой вероятности отказа - [V]LF позволяло бы обеспечивать требуемый уровень достоверности прогнозирования ресурса - DI. А затем по определить требуемое минимальное число значений каждой варьируемой переменной wk, чтобы число каждой wk в совокупности обеспечивали . И обеспечивали требуемый уровень достоверности прогнозирования ресурса – DI с учетом заданной допустимой вероятности отказа - [V]LF, соответствующей определенному уровню тяжести последствий - ULFi и требуемому уровню допустимого риска отказа - [R]LF.

Основываясь на полученных результатах исследований в соответствии с алгоритмом прогнозирования ресурса (рис. 3) разработан метод определения требуемого количества измерений параметров состояния, который основывается на расчете требуемого количества измерений параметров, являющихся варьируемыми переменными и определяющих достоверность прогнозируемого ресурса. Для этого в работе были теоретически обоснованы и экспериментально подтверждены зависимости для расчета и :

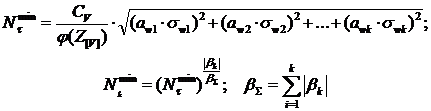, (13)

где: Z[V] – квантиль нормированного нормального распределения при значениях [V]LF; j( Z[V]) – плотность вероятности нормированного нормального распределения; sw1, sw2,…, swk - СКО выборок wk; awk и bk – коэффициенты регрессионных моделей (9) и (10) соответственно.

В соответствии с алгоритмом прогнозирования ресурса разработан метод определения требуемого состава методов диагностики параметров состояния. Метод основывается на выборе состава основных и дополнительных методов диагностики, сочетание которых позволяет обеспечить требуемый уровень достоверности диагностики – DM с использованием выполненной классификации методов по уровням достоверности диагностики параметров состояния.

Разработанный в соответствии с алгоритмом прогнозирования ресурса (рис. 3) метод расчета прогнозируемого ресурса (tS) основывается на вычислении tS по величине допустимого ресурса - tv и с учетом погрешности зависимости (9), уровней достоверности прогнозирования ресурса – DI, диагностики параметров состояния – DM и допустимого риска отказа - [R]LF. Вычислении tS выполняется по установленной зависимости:

, (14)

где: Dw - относительная ошибка зависимости (9), характеризующая связь между варьируемыми переменными и прогнозируемым ресурсом; nD – коэффициент, учитывающий уровни DI, DM и [R]LF. Значения nD = 1,1¸1,5 для DMH и DIH, nD=1,5¸2 для DMM и DIM. Минимальные значения nD принимаются для RLLF, максимальные значения nD для RHLF, средние значения для RMLF.

Метод определения требуемых мер по коррекции состояния и прогнозируемого ресурса в соответствии с алгоритмом (рис. 3) основывается на сравнении полученного расчетом значения прогнозируемого ресурса - tS со значением допустимого ([t]) нормативно установленного периода эксплуатации между экспертными обследованиями либо другим ограничением ресурса. При tS ³ [t] проведение коррекции состояния и результатов расчетов ресурса не требуется. При tS < [t], а также при низком уровне достоверности прогнозирования ресурса - DIL выполняется определение требуемых мер по коррекции состояния и результатов расчетов ресурса. Для этого путем повторных итераций расчета выполняется коррекция исходных данных и подбирается их набор, который позволяет обеспечить условие tS ³ [t]. Если это условие невыполнимо производится коррекция состояния, сбор данных о параметрах состояния и ресурса и повторный расчет. Исследованиями установлено, что в общем случае для коррекции исходных данных могут служить: повышение уровня [R]LF и введение в исходные данные для расчета повышенного значения [V]LF; повышение уровня достоверности – DI и введение в исходные данные повышенных значений количества контролируемых параметров состояния и ресурса; повышение уровня достоверности диагностики - DM путем учета в расчете дополнительного состава применяемых методов диагностики; повышение объема выборочного контроля - e путем введения в исходные данные повышенного значения e. В случае, если установленными мерами условияtS ³ [t] достичь не удается, методом итераций определяется сочетание мер которое приводит к наибольшему значению ресурса. Установленные возможные меры по коррекции результатов расчета учитываются при выборе мероприятий по коррекции данных о состоянии и коррекции состояния – дополнительному обследованию и восстановлению работоспособности оборудования. Сочетание мер, которое приводит к наибольшему значению ресурса, учитывается при проведении очередного обследования оборудования.

Разработана общая блок-схема алгоритма расчета прогнозируемого ресурса с использованием данных диагностического обследования и критериев допустимых вероятности и риска оборудования в период продлеваемого ресурса.

Результатами исследований было доказано, что прогнозирование ресурса с использованием разработанных и изложенных теоретических положений и методов прогнозирования ресурса должно опираться на информацию о показателях достоверности диагностики и совместных вариациях параметров состояния и ресурса. Часть этой исходной информации может быть получена по результатам диагностического обследования с применением методов и объемов контроля, установленных нормативными требованиями. Эти источники информации являются необходимыми, но не всегда достаточными. Поэтому объем требуемой или недостающей информации по требуемому количеству измерений параметров состояния также определяется с использованием разработанных теоретических положений и методов. Оценка достаточности и при необходимости дополнение требуемой информацией о показателях достоверности диагностики и совместных вариациях параметров состояния позволяет замкнуть задачу, выполнить прогнозирование ресурса и обеспечивать допустимые вероятность и риск отказа оборудования в период продлеваемого ресурса.

В пятой главе изложены результаты разработок нормативно - методического обеспечения и оценки эффективности применения методов прогнозирования ресурса.

Основываясь на результатах выполненных исследований и разработок теоретических положений, алгоритма и методов прогнозирования ресурса, был разработан новый нормативный документ - «Методические положения по прогнозированию ресурса безопасной эксплуатации оборудования объектов добычи и переработки сероводородсодержащих газа, конденсата, нефти с продлеваемым сроком безопасной эксплуатации». Методические положения устанавливают основные требования, алгоритм, принципы и порядок расчета прогнозируемого продлеваемого ресурса по данным диагностического обследования, в пределах которого обеспечиваются допустимый риск - [R]LF отказа. Обеспечение [R]LF осуществляется путем прогнозирования ресурса, отвечающего нормативно установленным значениям допустимой вероятности отказа - [V]LF с учетом показателей достоверности диагностики и совместных вариаций параметров состояния и ресурса.

В методических положениях изложены разработанные методические подходы, алгоритмы и методы определения показателей вариации параметров состояния и ресурса и построения В-модели прогнозируемого ресурса на основе сбора, анализа данных диагностического обследования, использования базы данных, полученных эмпирических зависимостей, зависимостей математической статистики и компьютерных программ математического и статистического анализов. Изложены принципы факторного анализа параметров состояния и ресурса методом главных компонент на ЭВМ с использованием компьютерной программы статистического анализа. Порядок расчета ресурса при совместных вариациях параметров состояния и ресурса на основе матричных вычислений с применением компьютерной программы математического анализа. Изложены методы оценки уровней тяжести последствий, уровней допустимого риска - [R]LF и определения значений допустимой вероятности отказа - [V]LF. Методы расчета допустимого ресурса - tv на основе статистического анализа выборки значений ресурса, полученной при совместных вариациях параметров состояния и ресурса. Методы построения эмпирической, интерполирующей, аппроксимирующей функций отказа и вычисления tv по критерию [V]LF. Методы оценки уровней достоверности прогнозирования ресурса и диагностики параметров состояния, определения требуемых количества измерений и состава методов диагностики параметров. Изложены порядок и методы расчета прогнозируемого ресурса и определения требуемых мер по коррекции состояния и ресурса.

Методическими положениями определены условия выбора перечня и сроков выполнения мероприятий по коррекции данных о состоянии элементов оборудования. Для практического применения разработанных методов и расчета прогнозируемого ресурса на ЭВМ были разработаны вычислительные блоки (модули): в программе Microsoft Excel – файлы, содержащие измеренные значения контролируемых параметров состояния; в программе Math Cad – файл «Расчет РБЭ. mcd», являющийся одновременно и алгоритмом программы расчета прогнозируемого ресурса и результатом ее выполнения; в программе STATISTICA - файлы ввода данных "М. sta", файл анализа и результатов факторного анализа "RgS. stw".

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5